【アミノ酸】等電点（求め方・pHとの関係・計算問題の解き方など）

2019年4月16日2023年6月23日

はじめに

【プロ講師解説】このページでは『【アミノ酸】等電点（求め方・pHとの関係・計算問題の解き方など）』について解説しています。

等電点とは

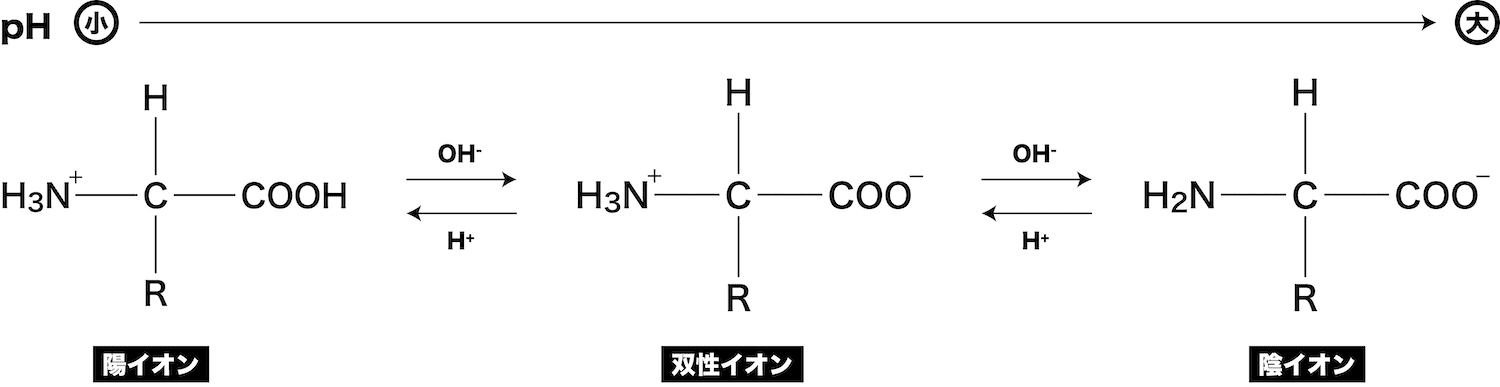
アミノ酸がもつ電荷は溶液のpHによって変化する。

参考：双性イオン（定義や特徴、酸・塩基との反応など）

アミノ酸のもつ正の電荷と負の電荷が釣り合ってアミノ酸全体として電荷をもたないpHを、そのアミノ酸の等電点という。
等電点では、ほぼ全てのアミノ酸が双性イオンになっており、少しだけ存在する陽イオンと陰イオンの数が等しく、全体で電荷は0になっている。

等電点一覧

代表的なアミノ酸の等電点は次の通りである。

中性アミノ酸

アミノ酸	等電点
グリシン	5.97
アラニン	6.00
セリン	5.68
フェニルアラニン	5.48
チロシン	5.66
システイン	5.07
メチオニン	5.74

酸性アミノ酸

アミノ酸	等電点
アスパラギン酸	2.77
グルタミン酸	3.22

塩基性アミノ酸

アミノ酸	等電点
リシン	9.74

大学入試では、中性アミノ酸の等電点は約6、酸性アミノ酸の等電点は約3、塩基性アミノ酸の等電点は約10と覚えていれば、基本的に問題ありません。

酸性・塩基性アミノ酸の等電点

酸性アミノ酸の等電点が酸性側に、塩基性アミノ酸の等電点が塩基性側に偏る理由について考える。

酸性アミノ酸の等電点

酸性アミノ酸はカルボキシ基を余分にもっている。

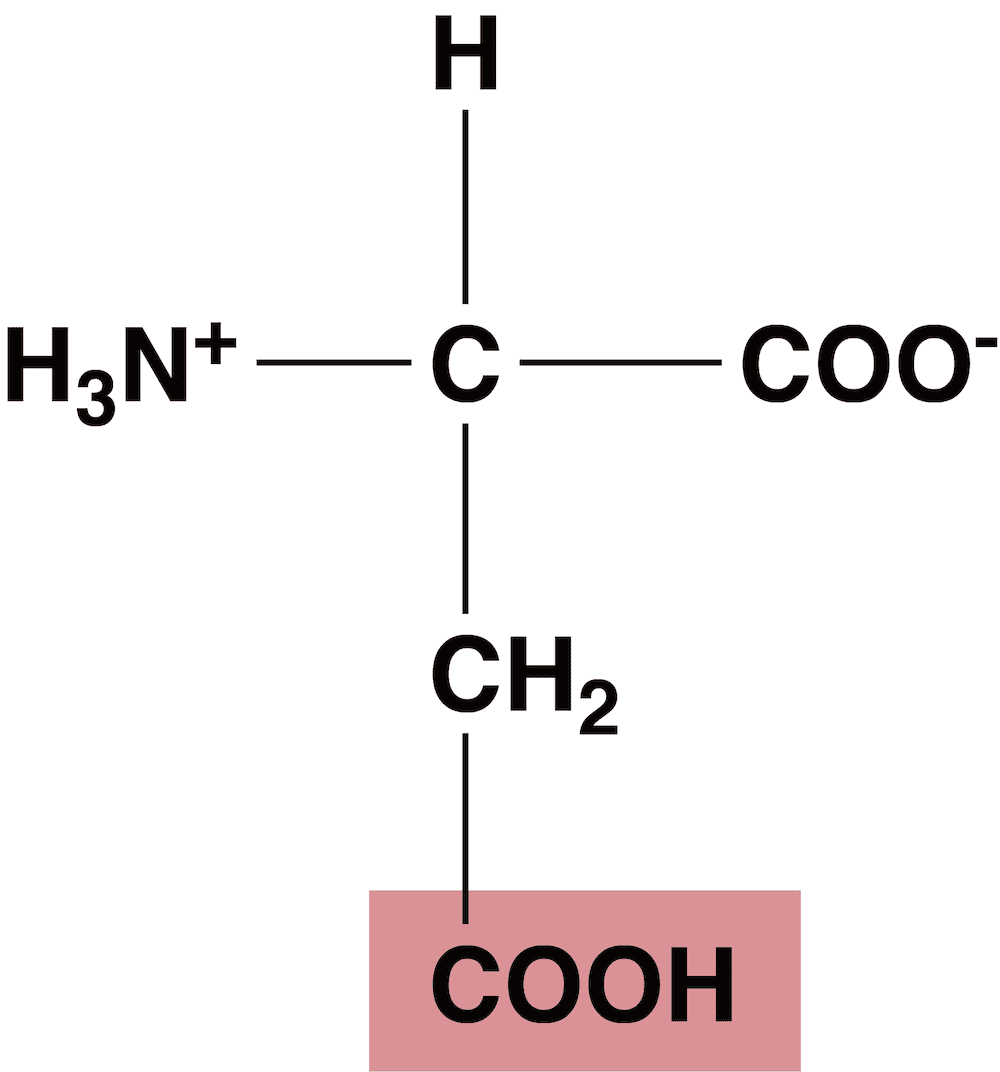
このカルボキシ基の電離を考えると…

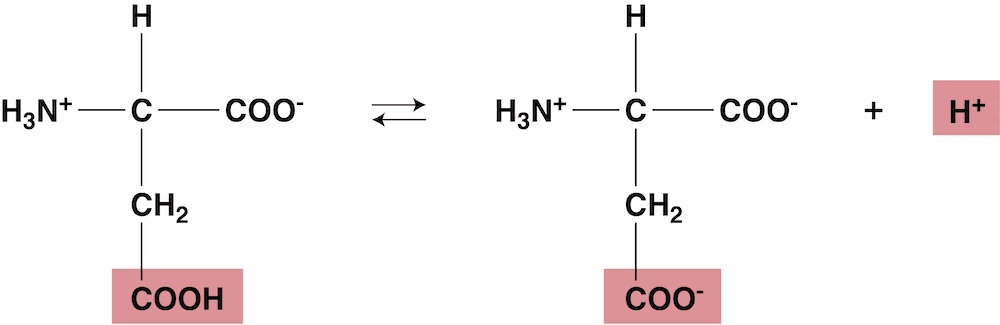
等電点ではほとんどのイオンが双性イオンになっているため、溶液中のH^＋濃度を大きくして（ルシャトリエの原理により）平衡を左に移動させた点が等電点となる。

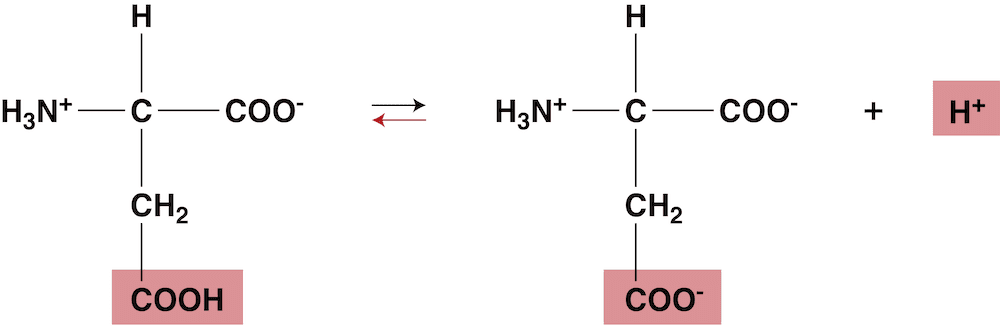
したがって、酸性アミノ酸の等電点は酸性側に偏る。

塩基性アミノ酸の等電点

塩基性アミノ酸はアミノ基を余分にもっている。

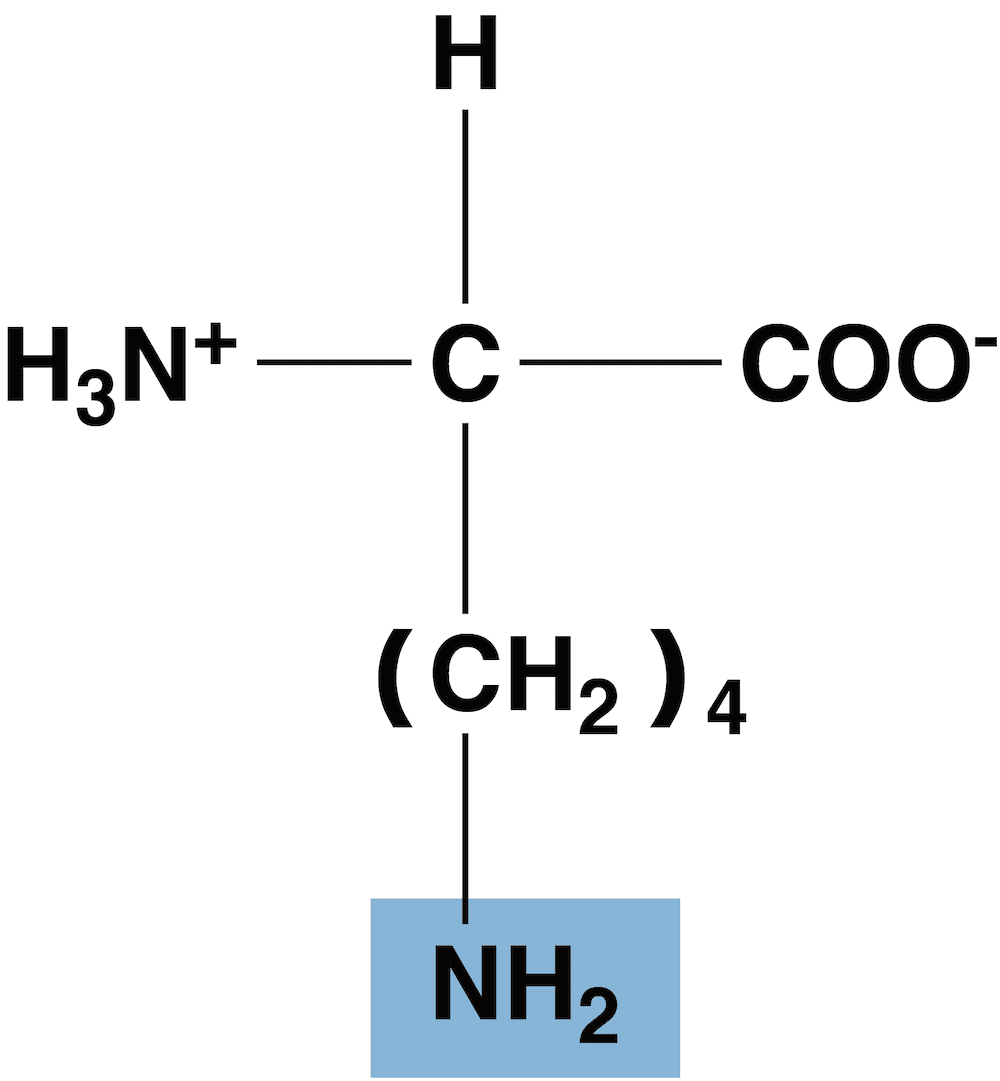
このアミノ基の水溶液中での反応を考えると…

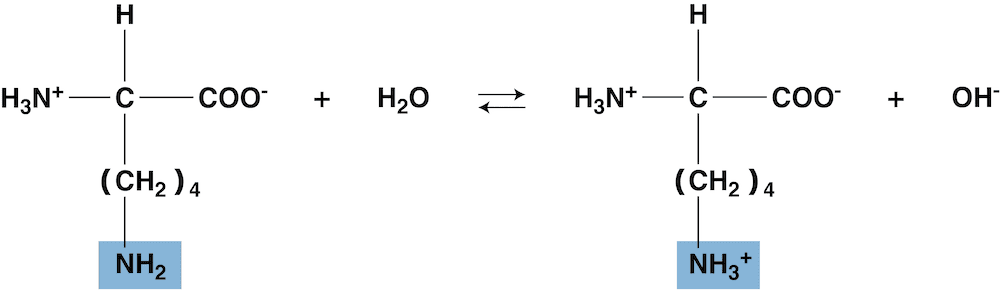
等電点ではほとんどのイオンが双性イオンになっているため、溶液中のOH^ー濃度を大きくして（ルシャトリエの原理により）平衡を左に移動させた点が等電点となる。

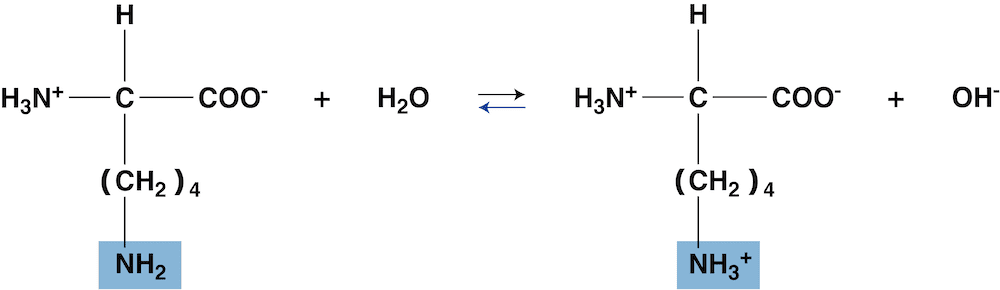
したがって、塩基性アミノ酸の等電点は塩基性側に偏る。

アミノ酸の分離

等電点の違いによりアミノ酸の混合物を分離することができる。
中性の水溶液でろ紙を湿らせ、真ん中に中性アミノ酸であるアラニン、酸性アミノ酸であるアスパラギン酸、塩基性アミノ酸であるリシンを含ませ電気泳動すると、次のようになる。

溶液のpHが等電点と等しいアラニンは電荷をもたないため移動しない。
それに対して、溶液のpHが等電点より大きいアスパラギン酸は負電荷をもつため陽極に、溶液のpHが等電点より小さいリシンは正電荷をもつため陰極に移動する。

参考：電気泳動（原理・中性/酸性/塩基性アミノ酸の移動方向など）

等電点の求め方

等電点の求め方に関する問題の解き方を解説する。

アミノ酸は溶液中で陽イオン・双性イオン・陰イオンが平衡状態になっています。平衡定数と等電点の関係を使った計算問題は入試頻出なのでここでしっかり確認しておきましょう。

問題

中性アミノ酸であるグリシンは水溶液中で次のような電離平衡状態にある。

\[ \begin{align}
&\underbrace{ \mathrm{H_{3}N^{+}-CH_{2}-COOH} }_{ \mathrm{A^{+}} } \overset{K_{1}}{\rightleftarrows}\underbrace{ \mathrm{H_{3}N^{+}-CH_{2}-COO^{-} }}_{ \mathrm{B} }\mathrm{+H^{+} }\\
&\underbrace{ \mathrm{H_{3}N^{+}-CH_{2}-COO^{-}} }_{\mathrm{ B} }\overset{K_{2}}{\rightleftarrows}\underbrace{ \mathrm{H_{2}N-CH_{2}-COO^{-}} }_{ \mathrm{C^{-}} }\mathrm{+H^{+}}
\end{align}\]

グリシンの等電点を求めなさい。ただし、K₁=1.0×10^ー2.3(mol/L)、K₂=1.0×10^ー9.7(mol/L)とする。

まずは上の式。

\[ \mathrm{A^{+} }\overset{K_{1}}{\rightleftarrows} \mathrm{B+H^{+}} \]

この式より、電離定数K₁は次のように表すことができる。

\[ K_{1}=\mathrm{\frac{ [B][H^{+}] }{ [A^{+}] }・・・①} \]

次に下の式。

\[ \mathrm{B} \overset{K_{2}}{\rightleftarrows} \mathrm{C^{-}+H^{+} }\]

この式より、電離定数K₂は次のように表すことができる。

\[ K_{2}=\mathrm{\frac{ [C^{-}][H^{+}] }{ [B] }・・・② }\]

このとき、①式×②式より…

\[ \begin{align}&K_{1}×K_{2}
\mathrm{=\frac{ \cancel{[B]} [H^{+}] }{ [A^{+}] } × \frac{ [C^{-}][H^{+}] }{ \cancel{[B]} }}\\
&\leftrightarrow K_{1}K_{2}\mathrm{=[H^{+}]^{2}×\frac{ [C^{-}]}{ [A^{+}] } }\end{align}\]