MENU
【pH計算】定義から公式、求め方、希釈や混合が絡む問題など
目次
はじめに
【プロ講師解説】このページでは『【pH計算】定義から公式、求め方、希釈や混合が絡む問題など』について解説しています。
pHとは
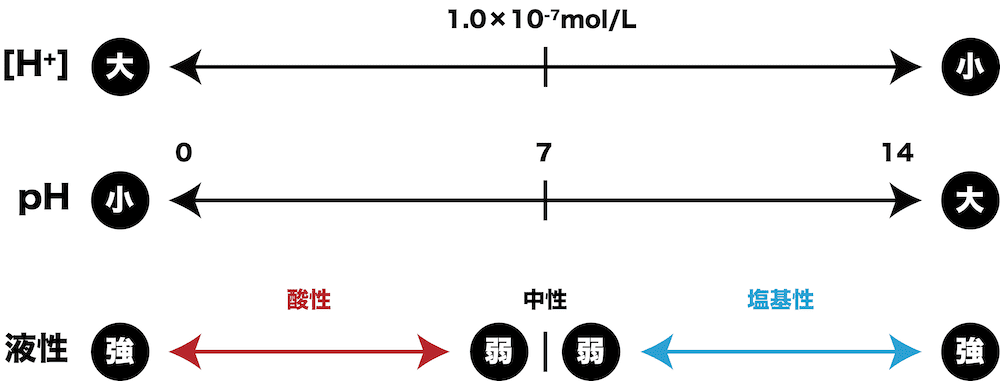
- 水溶液の液性は、水溶液中の水素イオンのモル濃度[H＋]で決まる。
- 25℃において、[H＋]と液性の関係は次のようになる。
| [H＋] | 液性 | |
|---|---|---|
| 純水と同じ | [H＋] = 1.0×10ー7(mol/L) | 中性 |
| 純水より大きい | [H＋] > 1.0×10ー7(mol/L) | 酸性 |
| 純水より小さい | [H＋] < 1.0×10ー7(mol/L) | 塩基性 |
- [H＋]は液性を考える上で重要な数値だが、値が小さく扱いづらい。そこで使うのが水素イオン指数（pH）である。
- [H＋]とpHには上のような関係がある。
\[ \begin{align}
&\mathrm{[H^{+}]=1.0×10^{-n}mol/L}\\
&\mathrm{→ pH=n}\end{align} \]
- したがって、[H＋]・液性・pHの関係をまとめると次のようになる。
| [H＋] | 液性 | pH |
|---|---|---|
| [H＋] = 1.0×10ー7(mol/L) | 中性 | 7 |
| [H＋] > 1.0×10ー7(mol/L) | 酸性 | < 7 |
| [H＋] < 1.0×10ー7(mol/L) | 塩基性 | > 7 |
logの使い方
- pH計算をする上で覚えておくべき数学の公式を紹介する。
\[ \begin{align}&\mathrm{①log_{10}A + log_{10}B = log_{10}AB}\\
&\mathrm{②log_{10}A – log_{10}B = log_{10}\frac{ A }{ B }}\\
&\mathrm{③log_{10}10^{A} = A} \end{align}\]
pH計算の公式
- pH計算をする上で覚えておくべき数学の公式を紹介する。
\[ \begin{align}&\mathrm{①pH = -log_{10}[H^{+}]}\\
&\mathrm{②pOH = -log_{10}[OH^{-}]}\\
&\mathrm{③[H^{+}][OH^{-}]=1.0×10^{-14}}\\
&\mathrm{④pH+pOH=14}\\
&\mathrm{⑤[H^{+}]=c×m×α}\\
&\mathrm{⑥[OH^{-}]=c×m×α} \end{align}\]
①pH = ーlog10[H＋]
\[ \begin{align}&\mathrm{[H^{+}]=1.0×10^{-n}}\\
&\mathrm{↔ -log_{10}[H^{+}]=-log_{10}10^{-n}(= n)}\\
&\mathrm{↔ pH=-log_{10}[H^{+}]} \end{align}\]
②pOH = ーlog10[OHー]
- pOHは水酸化物イオン指数であり、水溶液中の水酸化物イオンのモル濃度[OHー]との関係は次の通りである（①のOHバージョン！）。
\[ \mathrm{pOH = -log_{10}[OH^{-}]} \]
③[H＋][OHー] = 1.0×10ー14
- これは水のイオン積の公式である。
\[ \mathrm{[H^{+}][OH^{-}]=1.0×10^{-14}} \]
④pH + pOH = 14
- この公式は③を変形することで導出できる。
\[ \begin{align}&\mathrm{[H^{+}][OH^{-}]=1.0×10^{-14}}\\
&\mathrm{↔-log_{10}[H^{+}][OH^{-}]=-log_{10}1.0×10^{-14}}\\
&\mathrm{↔-( log_{10}[H^{+}]+log_{10}[OH^{-}] )=14}\\
&\mathrm{↔-log_{10}[H^{+}]-log_{10}[OH^{-}]=14}\\
&\mathrm{↔pH+pOH=14} \end{align}\]
⑤[H＋] = c×m×α
- 溶液のモル濃度cに価数m（酸がもっているH＋の数）と電離度α（溶解している酸に対する、電離している酸の割合）をかけると、H＋のモル濃度[H＋]を求めることができる。
\[ \mathrm{[H^{+}]=c×m×α} \]
参考：【酸・塩基】価数（一覧・覚え方・例など）
参考：電離度（求め方・公式・酸/塩基の強弱との関係など）
⑥[OHー] = c×m×α
- 溶液のモル濃度cに価数m（塩基がもっているOHーの数）と電離度α（溶解している塩基に対する、電離している塩基の割合）をかけると、OHーのモル濃度[OHー]を求めることができる。
\[ \mathrm{[OH^{-}]=c×m×α} \]
強酸のpHの求め方
- 強酸のpHの求め方を、例題を解きながら解説する。
問題
1.0×10ー２(mol/L)の塩酸のpHを求めよ。ただし、塩酸の電離度は1とする。（有効数字2桁で解答）
STEP
[H＋]=c×m×αより、[H＋]を求める。
まずは、[H＋]=c×m×αの公式を使って、[H＋]を求める。
\[ \begin{align} \mathrm{[H^{+}]} &\mathrm{= 1.0×10^{-2}×1×1} \\
&\mathrm{= 1.0×10^{-2}} \end{align} \]
STEP
pH=ーlog[H＋]より、pHを求める。
次に、pH=ーlog[H＋]の公式を使って、pHを求める。
\[ \begin{align} \mathrm{pH}&\mathrm{=-log(1.0×10^{-2})} \\
&\mathrm{= 2.0} \end{align} \]
弱酸のpHの求め方
- 弱酸のpHの求め方を、例題を解きながら解説する。
問題
0.10×10ー3(mol/L)の酢酸のpHを求めよ。ただし、酢酸の電離度は0.01とする。（有効数字2桁で解答）
STEP
[H＋]=c×m×αより、[H＋]を求める。
まずは、[H＋]=c×m×αの公式を使って、[H＋]を求める。
\[ \begin{align} \mathrm{[H^{+}]}&\mathrm{=0.10×10^{-3} × 1 × 0.01} \\
&\mathrm{=1.0×10^{-6}} \end{align} \]
STEP
pH=ーlog[H＋]より、pHを求める。
次に、pH=ーlog[H＋]の公式を使って、pHを求める。
\[ \begin{align} \mathrm{pH}&\mathrm{=-log(1.0×10^{-6})} \\
&\mathrm{=6.0} \end{align} \]
強塩基のpHの求め方
- 強塩基のpHの求め方を、例題を解きながら解説する。
問題
1.0×10ー2(mol/L)の水酸化ナトリウム水溶液のpHを求めよ。ただし、水酸化ナトリウムの電離度は1とする。（有効数字2桁で解答）
STEP
[OHー]= c×m×αより、[OHー]を求める。
まずは、[OHー]=c×m×αの公式を使って、[OHー]を求める。
\[ \begin{align} \mathrm{[OH^{-}]}&\mathrm{=1.0×10^{-2}×1×1}\\
&\mathrm{=1.0×10^{-2}} \end{align} \]
STEP
[H＋][OHー]=1.0×10ー14より、[H＋]を求める。
次に、[H＋][OHー]=1.0×10ー14の公式を使って、[H＋]を求める。
\[ \begin{align}\mathrm{ [H^{+}]}&\mathrm{=\frac{ 1.0×10^{-14} }{ [OH^{-}] }}\\
&\mathrm{=\frac{ 1.0×10^{-14} }{ 1.0×10^{-2} }}\\
&\mathrm{=1.0×10^{-12}}\end{align} \]
STEP
pH=ーlog[H＋]より、pHを求める。
最後に、pH=ーlog[H＋]の公式を使って、pHを求める。
\[ \begin{align} \mathrm{pH}&\mathrm{=-log(1.0×10^{-12})}\\
&\mathrm{=12} \end{align} \]
希釈溶液のpH計算
- 希釈溶液とは元々あった溶液を薄めた溶液である。
- pHの計算問題では、この希釈溶液の関連の問題がよく出題されるため、解き方をきちんと定着させておこう。
問題
1.0×10ー２(mol/L)の塩酸HCl1.0mlに水を加え、全体で100mlとした。このときのpHを求めよ。ただし、HClの電離度は1とする。（有効数字2桁で解答）
STEP
希釈前のmolを求める。
まずは、希釈前のmolを求める。
\[ \mathrm{1.0×10^{-2}(mol/L) × \frac{ 1 }{ 1000 }(L) = 1.0×10^{-5}(mol)} \]
STEP
そのmolを、希釈後のLで割ることでモル濃度(mol/L)を求める。
次に、STEP1で求めたmolをLで割ることにより、濃度を導き出す。
そのmolを、希釈後のLで割ることでモル濃度(mol/L)を求める。
\[ \mathrm{\frac{ 1.0×10^{-5}(mol) }{ \displaystyle \frac{ 100 }{ 1000 }(L) } = 1.0×10^{-4}(mol/L)} \]
STEP
[H＋]=c×m×αより、[H＋]を求める。
次に、[H＋]=c×m×αの公式を使って、[H＋]を求めていく。
\[ \begin{align} \mathrm{[H^{+}]}&\mathrm{=1.0×10^{-4} ×1×1}\\
&\mathrm{=1.0×10^{-4}} \end{align} \]
STEP
pH=ーlog[H＋]からpHを求める。
次に、pH=ーlog[H＋]の公式を使って、pHを求めていく。
\[ \begin{align}\mathrm{ pH}&\mathrm{=-log(1.0×10^{-4})}\\
&\mathrm{=4.0} \end{align} \]
混合溶液のpH計算
- 混合溶液とは複数の溶液を混ぜてできる溶液である。
- 混合溶液のpH計算も、希釈溶液のpH計算同様入試頻出なので、解き方をきちんと定着させておこう。
問題
1.0×10−2(mol/L)の塩酸HCI 10mlに、1.0×10−3(mol/L)の水酸化ナトリウムNaOH水溶液10mLを加えた。このときのpHを求めよ。ただし、log104.5＝0.65とする。
STEP
酸から生じるH＋、塩基から生じるOHー、それぞれのmolを求める。
まずは、HClから生じるH＋、NaOHから生じるOHーのmolをそれぞれ求める。
HClから生じるH＋
\[ \begin{align}\mathrm{H^{+}}&\mathrm{=1.0×10^{-2}(mol/L)×\frac{ 10 }{ 1000 }(L)×1}\\
&\mathrm{=1.0×10^{-4}(mol)} \end{align} \]
NaOHから生じるOHー
\[ \begin{align}\mathrm{OH^{-}}&\mathrm{=1.0×10^{-3}(mol/L)×\frac{ 10 }{ 1000 }(L)×1}\\
&\mathrm{=1.0×10^{-5}(mol) }\end{align} \]
STEP
STEP1で求めたmol同士で値が正になるように引き算し、中和できずに余ったH＋（またはOHー）のmolを求める。
次に、STEP1で求めたmol同士で引き算することで、中和で余ったH＋（またはOHー）のmolを求める。
\[ \underbrace{ 1.0×10^{-4}}_{ \mathrm{HClから出たH^{+}} } – \underbrace{ 1.0×10^{-5}}_{ \mathrm{NaOHから出たOH^{-}} }
=\underbrace{ 9.0×10^{-5}}_{ \mathrm{余ったH^{+}} } \]
STEP
STEP2で求めた値をLで割り、H＋の濃度（[H＋]）を求める。
次に、STEP2で求めたmolをLで割ることにより、H＋の濃度を導き出す。
\[ \mathrm{\frac{ 9.0×10^{-5}(mol) }{ \displaystyle \frac{ 10+10 }{ 1000 }(L) } = 4.5×10^{-3}(mol/L)} \]
STEP
[H＋]の値をpH=ーlog10[H＋]に代入し、pHを求める。
最後に、pH=ーlog[H＋]の公式を使って、pHを求める。
\[ \begin{align} \mathrm{pH}&\mathrm{=-log(4.5×10^{-3})}\\
&=2.35\\
&≒2.4 \end{align} \]
【新課程対応】化学の計算ドリル大好評発売中！
高校化学・化学基礎の計算問題が苦手な人に向けた計算ドリルを発売しました。豊富な問題数で、入試頻出の計算問題の解き方を身につけることができます。
【新課程対応】無機化学ドリル発売中！
無機化学の知識を総ざらいできるオリジナル問題集ができました。解答・解説編には入試頻出事項が一通りまとめられており、まとめノート/参考書としての役割も果たします。
【新課程対応】有機化学ドリル発売中！
有機化学に関する入試頻出事項を演習することのできるオリジナル問題集が紙の本になりました。暗記項目だけではなく、計算問題や思考力が問われる問題についても触れています。
