逆滴定（例題・計算問題の解き方・原理など）

【プロ講師解説】このページでは『中和滴定の一種である逆滴定（例題・計算問題の解き方・原理など）』について解説しています。解説は高校化学・化学基礎を扱うウェブメディア『化学のグルメ』を通じて6年間大学受験に携わるプロの化学講師が執筆します。

逆滴定とは

特殊な中和滴定

Point!

気体（例：アンモニア）など、通常の中和滴定を行いにくい物質を滴定するための特殊な滴定法を逆滴定という。

逆滴定の流れ

逆滴定の流れについて「アンモニアの逆滴定」を例に説明していこう。

まず始めに、酸である「硫酸H₂SO₄」を大量に用意する。

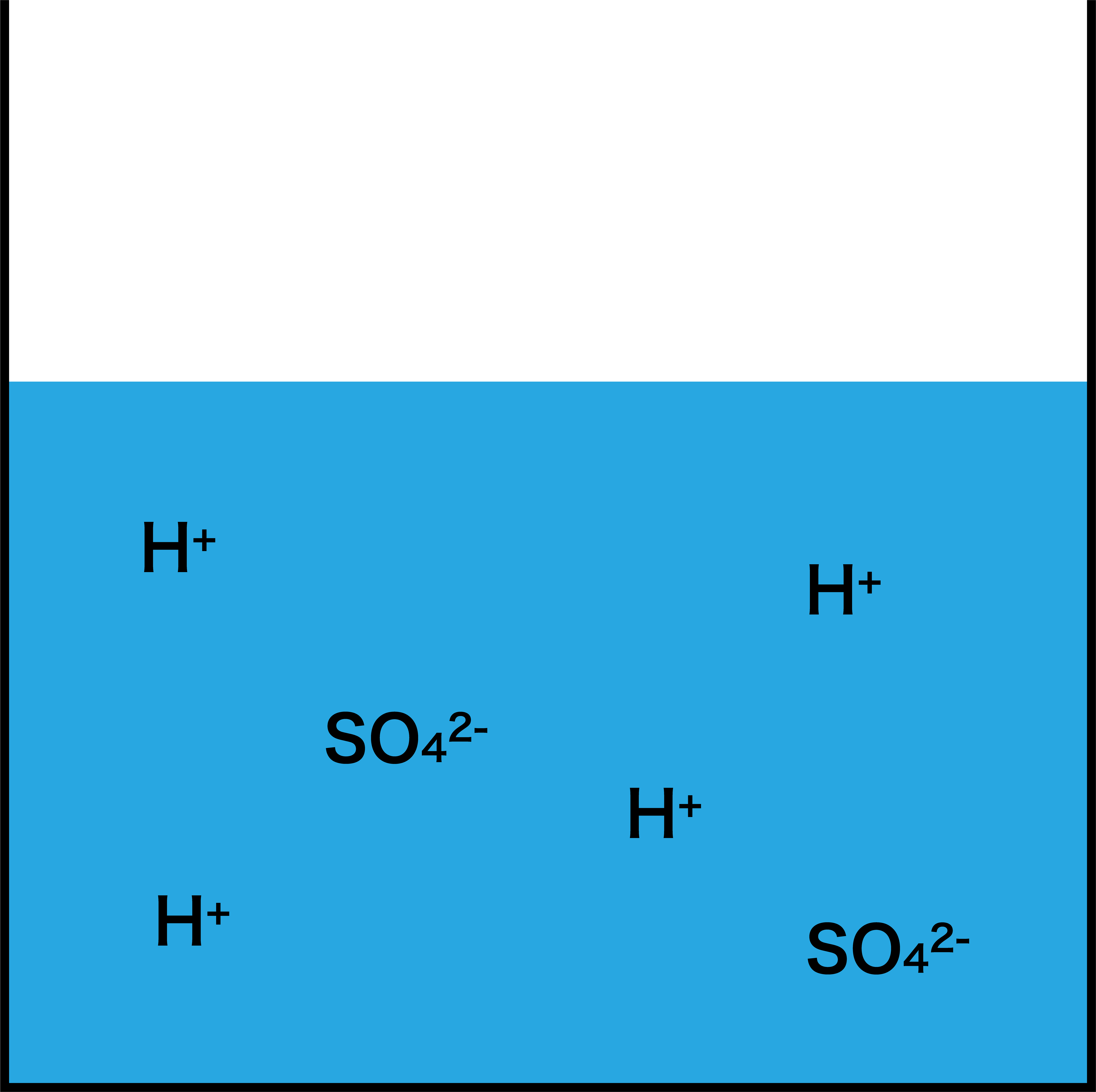
ここにアンモニアNH₃を完全に吸収させる。

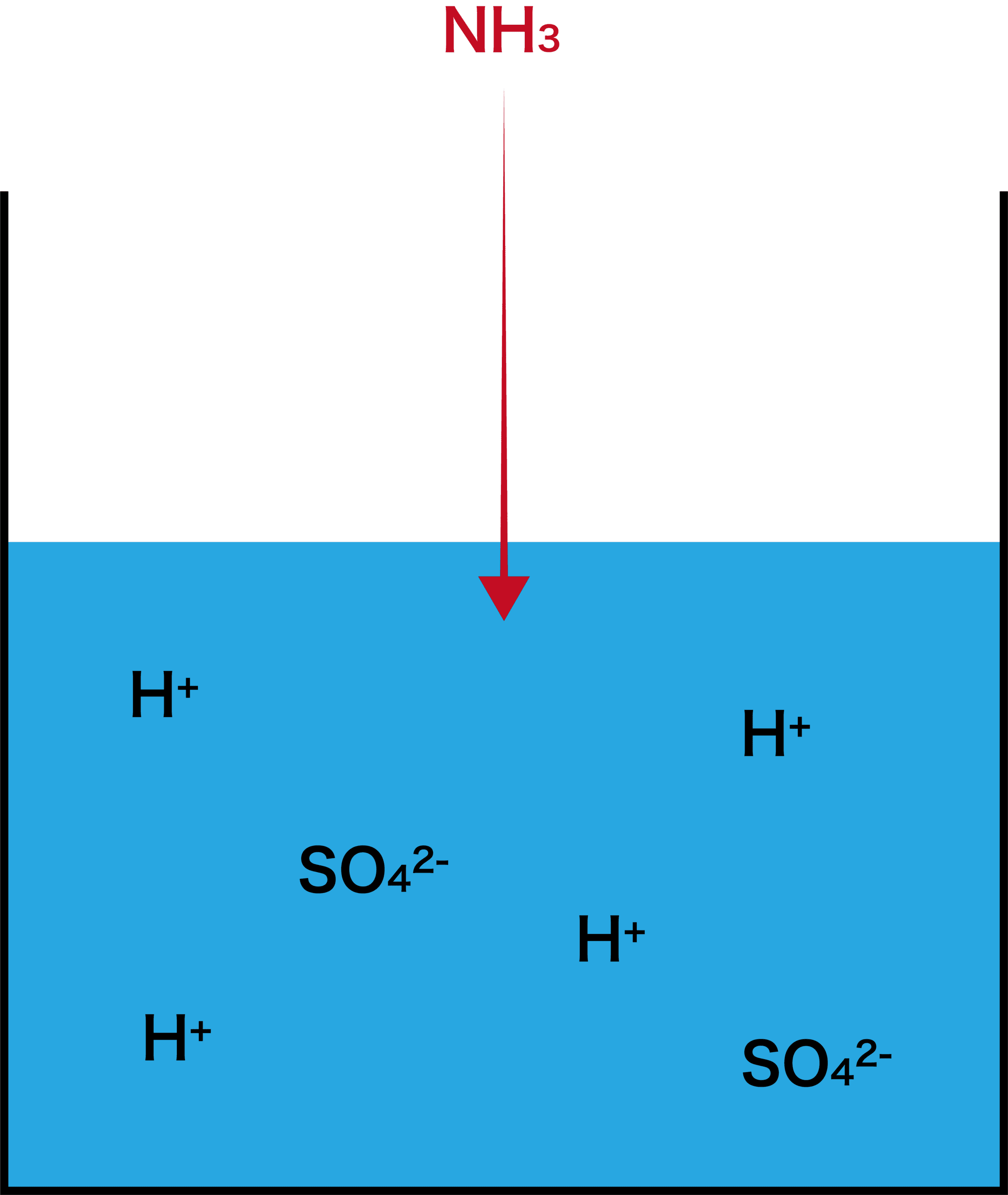
すると、NH₃は水中に存在するH⁺の一部と反応してNH₄⁺になる。

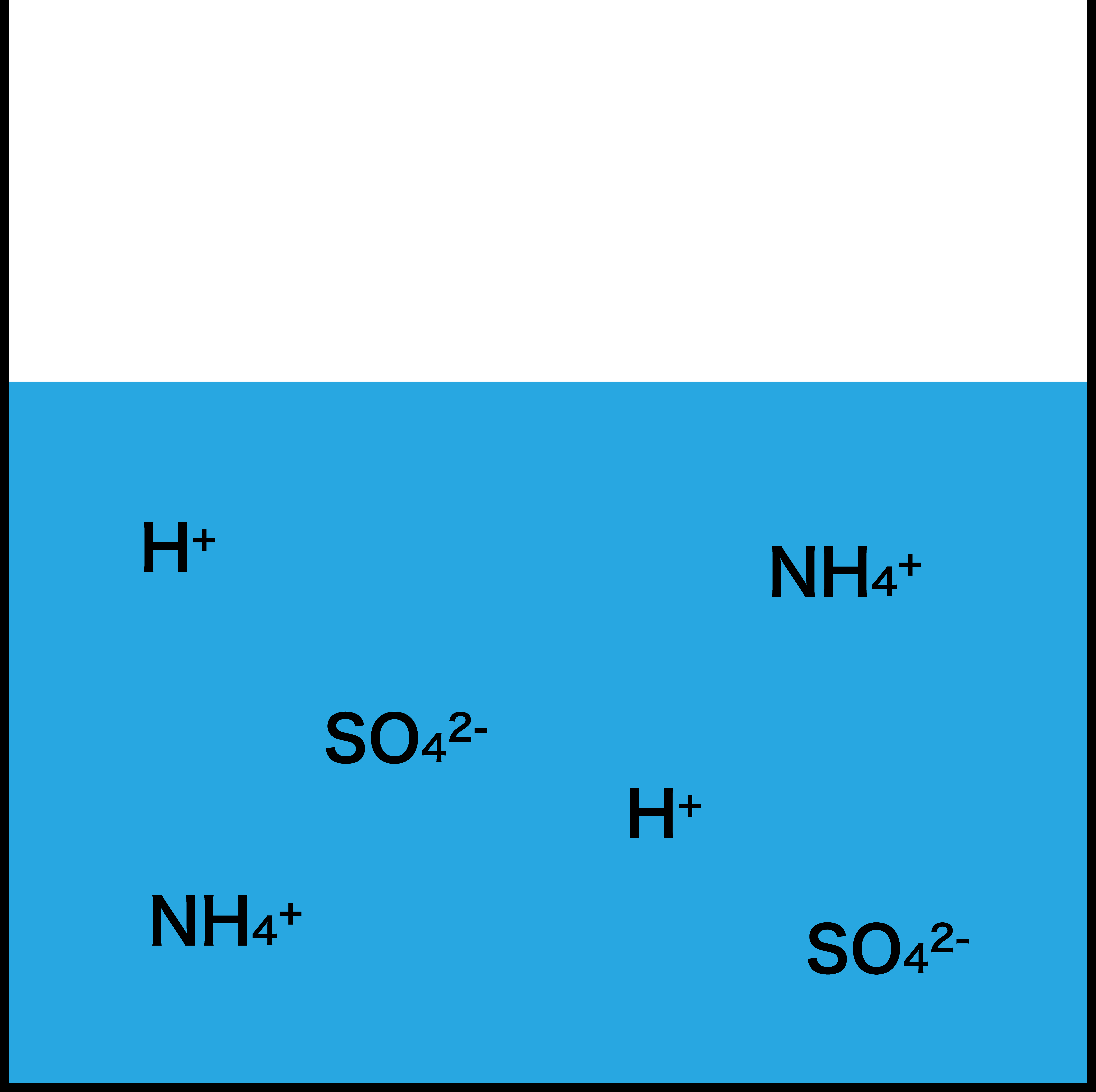
ここに指示薬（メチルオレンジorメチルレッド）を入れ、先ほどNH₃と反応しなかったH⁺を水酸化ナトリウムNaOHで滴定する。

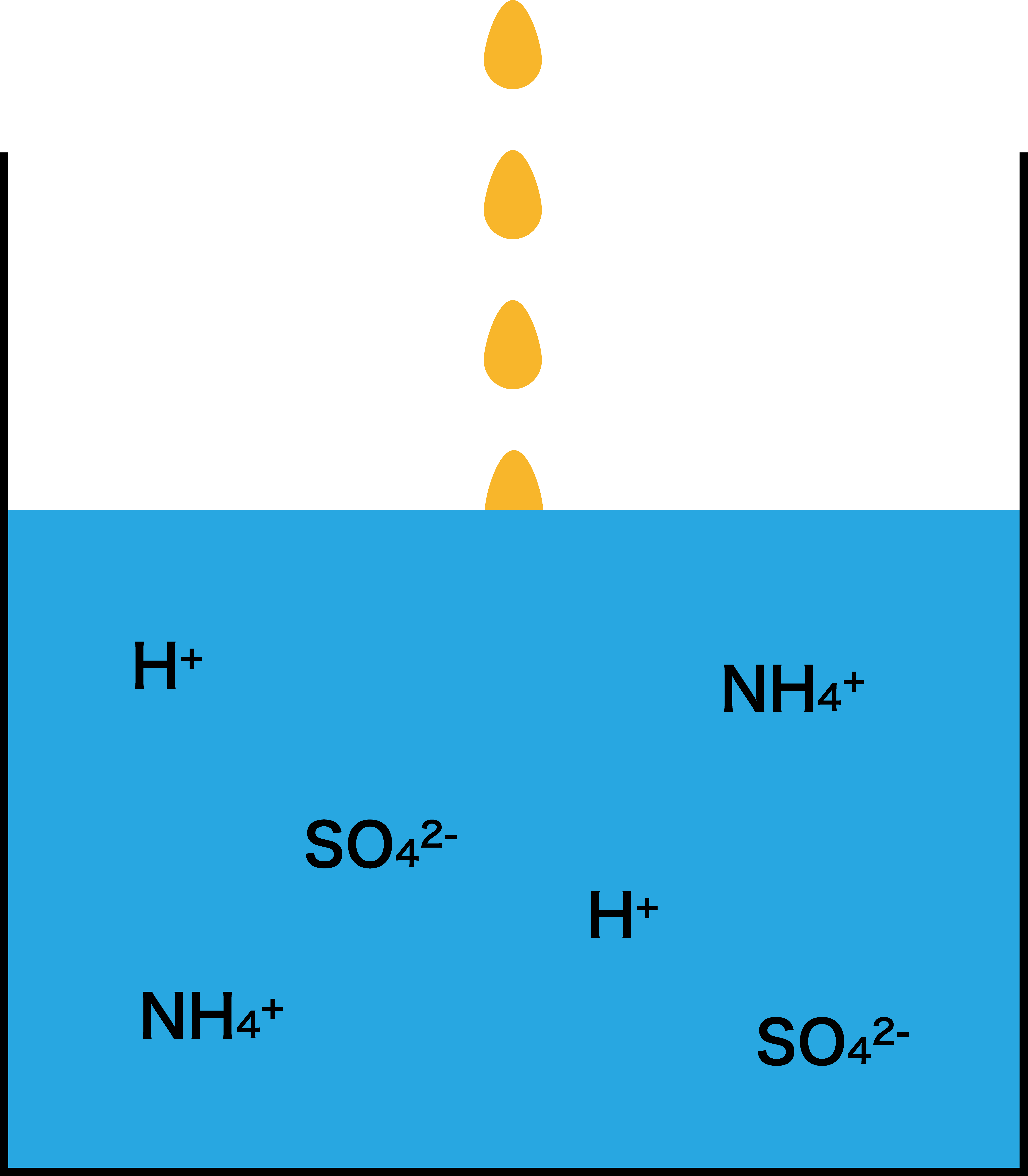
徐々に中和されていき…

完全に中和したときこのような状態になる。
H⁺はすべてOH^–と合わさり水になっている。（Na⁺は省略）

これが、逆滴定の流れである。要するに、酸である硫酸を２つの塩基（水酸化ナトリウム、アンモニア）で滴定しているということである。

それでは、この実験からアンモニアの濃度を求める計算問題の解き方を解説していこう。

逆滴定計算の流れ

問題

0.50(mol/L)の硫酸200(ml)に、100(ml)のアンモニアを吸収させた。その後、1.0(mol/L)の水酸化ナトリウムで滴定したところ20(ml)滴下した所で色が変化した。アンモニアの濃度(mol/L)を求めよ。

STEP1	直線を書き、数値を並べる
STEP2	中和計算をする

Point!

これが逆滴定王道の２STEP。この通りやれば、逆滴定の問題はほぼ必ず解くことができる。

STEP1

直線を書き数値を並べる。

まずは、直線を書き数値を並べる。

酸と塩基で上下に分けて、それぞれの物質とそのmol/L、Lを書き並べる。

STEP2

中和計算をする。

次に、STEP1で作った直線を使って中和計算をしていく。

【公式あり】中和計算を一瞬で解く方法を理由を交えて徹底解説！でやったように、中和点で酸と塩基のmol数が等しくなることを利用して計算式を立てよう。

\[
\underbrace{ 0.50(mol/L) × \frac{ 200 }{ 1000 }(L) × 2 }
_{ H_{2}SO_{4}\text{ の放出する }H^{+}\text{ のmol }}
=
\underbrace{ 1.0(mol/L) × \frac{ 20 }{ 1000 }(L) × 1 }
_{ NaOH\text{ の受け取る }H^{+}\text{ のmol }}
+
\underbrace{ x(mol/L) × \frac{ 100 }{ 1000 }(L) × 1 }
_{ NH_{3}\text{ の受け取る }H^{+}\text{ のmol }} \\
↔︎ x=1.8(mol/L)
\]

価数をかけるのを忘れないように。

計算演習

問１

濃度不明のアンモニア400(ml)の濃度を調べるために以下の実験を行った。
【実験】1.0(mol/L)の硫酸200(ml)にアンモニアをすべて溶かした。その後、この溶液に0.50(mol/L)の水酸化ナトリウムを滴下した。すると、200(ml)加えたところで完全に中和した。
このときのアンモニアの濃度は何(mol/L)か。

【問１】解答/解説：タップで表示

解答：0.75(mol/L)

\[
\underbrace{ 1.0(mol/L) × \frac{ 200 }{ 1000 }(L) × 2 }
_{ H_{2}SO_{4}\text{ の放出する }H^{+}\text{ のmol }}
=
\underbrace{ 0.50(mol/L) × \frac{ 200 }{ 1000 }(L) × 1 }
_{ NaOH\text{ の受け取る }H^{+}\text{ のmol }}
+
\underbrace{ x(mol/L) × \frac{ 400 }{ 1000 }(L) × 1 }
_{ NH_{3}\text{ の受け取る }H^{+}\text{ のmol }} \\
↔︎ x=0.75(mol/L)
\]

問２

濃度不明のアンモニア200(ml)の濃度を調べるために以下の実験を行った。
【実験】2.0(mol/L)の硫酸100(ml)にアンモニアをすべて溶かした。その後、この溶液に0.5(mol/L)の水酸化ナトリウムを滴下した。すると、40(ml)加えたところで完全に中和した。
このときのアンモニアの濃度は何(mol/L)か。

【問２】解答/解説：タップで表示

解答：1.9(mol/L)

\[
\underbrace{ 2.0(mol/L) × \frac{ 100 }{ 1000 }(L) × 2 }
_{ H_{2}SO_{4}\text{ の放出する }H^{+}\text{ のmol }}
=
\underbrace{ 0.50(mol/L) × \frac{ 40 }{ 1000 }(L) × 1 }
_{ NaOH\text{ の受け取る }H^{+}\text{ のmol }}
+
\underbrace{ x(mol/L) × \frac{ 200 }{ 1000 }(L) × 1 }
_{ NH_{3}\text{ の受け取る }H^{+}\text{ のmol }} \\
↔︎ x=1.9(mol/L)
\]