【プロ講師解説】このページでは『中和計算（中和滴定の計算）の仕組みや入試で即使える公式など』について解説しています。解説は高校化学・化学基礎を扱うウェブメディア『化学のグルメ』を通じて6年間大学受験に携わるプロの化学講師が執筆します。

中和とは

H+のmol＝OH–のmol
Point!

酸と塩基が反応すると、塩と水H2Oが生じる。この反応を中和という。

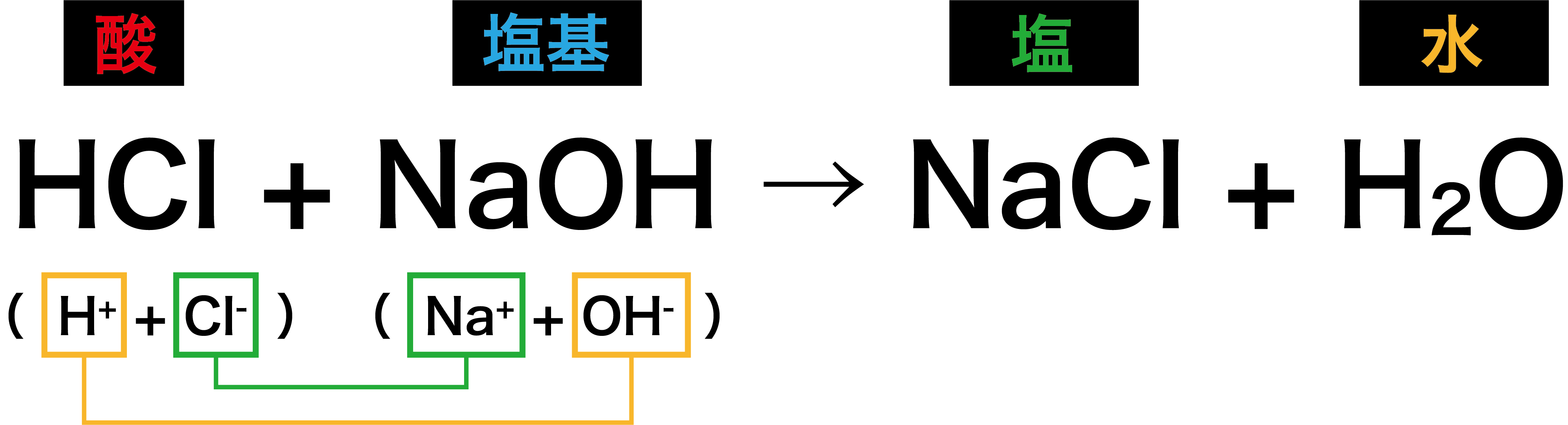
中和したとき、酸のもつH+と塩基のもつOH–が１コずつ組み合わさりH2Oが生じる。したがって、「中和をする＝酸由来のH+と塩基由来のOH–が等しくなる」と考えることができる。

酸に含まれるH+・塩基に含まれるOH–

硫酸H2SO4が1molあるとき、そこに含まれるH+は何molだろうか。

H2SO4は２価の酸なので、含まれているH+の物質量（mol）はH2SO4の物質量（mol）の２倍。

したがって…

\[
1(mol) × 2 = 2(mol)
\]

このようになる。

つまり、酸がもつH+の物質量（mol）は「酸の物質量（mol）×酸の価数」で求めることができるということである。

同様に、塩基がもつOH–の物質量（mol）は「塩基の物質量（mol）×塩基の価数」で求めることができる。

以上の説明を踏まえると、中和点における酸・塩基の関係は次の式で表すことができる。

酸のmol×酸の価数＝塩基のmol×塩基の価数
Point!

中和計算

それでは、上で紹介した式を使って実際に中和の計算問題を解いていこう。

問題

0.10(mol/L)の硫酸H2SO42.0(L)を中和するために必要な0.20(mol/L)の水酸化ナトリウムNaOHは何(L)か。

中和の計算式に問題文で与えられている数値を当てはめよう。

酸のmol×酸の価数＝塩基のmol×塩基の価数
Point!
\[
\underbrace{ 0.10(mol/L) × 2.0(L) }
_{ H_{2}SO_{4}\text{ のmol }}
×
\underbrace{ 2 }
_{ \text{ 価数 }}
=
\underbrace{ 0.20(mol/L) × x(L) }
_{ NaOH\text{ のmol }}
×
\underbrace{ 1 }
_{ \text{ 価数 }} \\
↔︎ x=2.0(L)
\]

計算演習

問１

0.20(mol/L)の塩酸HCl10(L)を中和するのに必要な0.40(mol/L)の水酸化ナトリウムNaOH水溶液は何(L)か。
【問１】解答/解説：タップで表示
解答：5.0(L)

公式に当てはめよう。

\[
\underbrace{ 0.20(mol/L) × 10(L) }
_{ HCl\text{ のmol }}
×
\underbrace{ 1 }
_{ \text{ 価数 }}
=
\underbrace{ 0.40(mol/L) × x(L) }
_{ NaOH\text{ のmol }}
×
\underbrace{ 1 }
_{ \text{ 価数 }} \\
↔︎ x=5.0(L)
\]

問２

0.10(mol/L)の塩酸HCl2.0(L)を中和するのに必要な0.20(mol/L)の水酸化ナトリウムNaOH水溶液は何(L)か。
【問２】解答/解説：タップで表示
解答：1.0(L)

公式に当てはめよう。

\[
\underbrace{ 0.10(mol/L) × 2.0(L) }
_{ HCl\text{ のmol }}
×
\underbrace{ 1 }
_{ \text{ 価数 }}
=
\underbrace{ 0.20(mol/L) × x(L) }
_{ NaOH\text{ のmol }}
×
\underbrace{ 1 }
_{ \text{ 価数 }} \\
↔︎ x=1.0(L)
\]

問３

0.40(mol/L)の塩酸HCl500(mL)を中和するのに必要な0.20(mol/L)の水酸化ナトリウムNaOH水溶液は何(L)か。
【問３】解答/解説：タップで表示
解答：1.0(L)

公式に当てはめよう。500(mL)は分数にして(L)で表そう。

\[
\underbrace{ 0.40(mol/L) × \frac{ 500 }{ 1000 }(L) }
_{ HCl\text{ のmol }}
×
\underbrace{ 1 }
_{ \text{ 価数 }}
=
\underbrace{ 0.20(mol/L) × x(L) }
_{ NaOH\text{ のmol }}
×
\underbrace{ 1 }
_{ \text{ 価数 }} \\
↔︎ x=1.0(L)
\]

問４

0.20(mol/L)の硫酸H2SO42.0(L)を中和するのに必要な0.20(mol/L)の水酸化ナトリウムNaOH水溶液は何(L)か。
【問４】解答/解説：タップで表示
解答：4.0(L)

公式に当てはめよう。

\[
\underbrace{ 0.20(mol/L) × 2.0(L) }
_{ H_{2}SO_{4}\text{ のmol }}
×
\underbrace{ 2 }
_{ \text{ 価数 }}
=
\underbrace{ 0.20(mol/L) × x(L) }
_{ NaOH\text{ のmol }}
×
\underbrace{ 1 }
_{ \text{ 価数 }} \\
↔︎ x=4.0(L)
\]

問５

0.30(mol/L)の水酸化ナトリウムNaOH水溶液2.0(L)を中和するのに必要な0.20(mol/L)の硫酸H2SO4は何(L)か。
【問５】解答/解説：タップで表示
解答：1.5(L)

公式に当てはめよう。

\[
\underbrace{ 0.20(mol/L) × x(L) }
_{ H_{2}SO_{4}\text{ のmol }}
×
\underbrace{ 2 }
_{ \text{ 価数 }}
=
\underbrace{ 0.30(mol/L) × 2.0(L) }
_{ NaOH\text{ のmol }}
×
\underbrace{ 1 }
_{ \text{ 価数 }} \\
↔︎ x=1.5(L)
\]

問６

0.10(mol/L)の塩酸HCl1.0(L)を中和するために水酸化ナトリウムNaOH水溶液を加えていった。すると2.0(L)加えたところでちょうど中和された。このとき加えた水酸化ナトリウムNaOH水溶液の濃度は何(mol/L)か。
【問６】解答/解説：タップで表示
解答：0.050(mol/L)

公式に当てはめよう。

\[
\underbrace{ 0.10(mol/L) × 1.0(L) }
_{ HCl\text{ のmol }}
×
\underbrace{ 1 }
_{ \text{ 価数 }}
=
\underbrace{ x(mol/L) × 2.0(L) }
_{ NaOH\text{ のmol }}
×
\underbrace{ 1 }
_{ \text{ 価数 }} \\
↔︎ x=0.050(mol/L)
\]

問７

0.050(mol/L)の硫酸H2SO44.0(L)を中和するために水酸化ナトリウムNaOH水溶液を加えていった。すると1.0(L)加えたところでちょうど中和された。このとき加えた水酸化ナトリウムNaOH水溶液の濃度は何(mol/L)か。
【問７】解答/解説：タップで表示
解答：0.40(mol/L)

公式に当てはめよう。

\[
\underbrace{ 0.050(mol/L) × 4.0(L) }
_{ H_{2}SO_{4}\text{ のmol }}
×
\underbrace{ 2 }
_{ \text{ 価数 }}
=
\underbrace{ x(mol/L) × 1.0(L) }
_{ NaOH\text{ のmol }}
×
\underbrace{ 1 }
_{ \text{ 価数 }} \\
↔︎ x=0.40(mol/L)
\]

問８

0.20(mol/L)の水酸化カルシウムCa(OH)2水溶液3.0(L)を中和するために硫酸H2SO4を加えていった。すると1.0(L)加えたところでちょうど中和された。このとき加えた硫酸H2SO4の濃度は何(mol/L)か。
【問８】解答/解説：タップで表示
解答：0.60(mol/L)

公式に当てはめよう。

\[
\underbrace{ x(mol/L) × 1.0(L) }
_{ H_{2}SO_{4}\text{ のmol }}
×
\underbrace{ 2 }
_{ \text{ 価数 }}
=
\underbrace{ 0.20(mol/L) × 3.0(L) }
_{ Ca(OH)_{2}\text{ のmol }}
×
\underbrace{ 2 }
_{ \text{ 価数 }} \\
↔︎ x=0.60(mol/L)
\]

問９

0.10(mol/L)の水酸化バリウムBa(OH)2水溶液200(ml)を中和するために硫酸H2SO4を加えていった。すると4.0(L)加えたところでちょうど中和された。このとき加えた硫酸H2SO4の濃度は何(mol/L)か。
【問９】解答/解説：タップで表示
解答：0.0050(mol/L)

公式に当てはめよう。

\[
\underbrace{ x(mol/L) × 4.0(L) }
_{ H_{2}SO_{4}\text{ のmol }}
×
\underbrace{ 2 }
_{ \text{ 価数 }}
=
\underbrace{ 0.10(mol/L) × \frac{ 200 }{ 1000 }(L) }
_{ Ba(OH)_{2}\text{ のmol }}
×
\underbrace{ 2 }
_{ \text{ 価数 }} \\
↔︎ x=0.0050(mol/L)
\]

問１０

0.050(mol/L)の塩酸HCl4.0(L)を中和するために水酸化ナトリウムNaOH水溶液を加えていった。すると2.0(L)加えたところでちょうど中和された。このとき加えた水酸化ナトリウムNaOH水溶液の濃度は何(mol/L)か。
【問１０】解答/解説：タップで表示
解答：0.10(mol/L)

公式に当てはめよう。

\[
\underbrace{ 0.050(mol/L) × 4.0(L) }
_{ HCl\text{ のmol }}
×
\underbrace{ 1 }
_{ \text{ 価数 }}
=
\underbrace{ x(mol/L) × 2.0(L) }
_{ NaOH\text{ のmol }}
×
\underbrace{ 1 }
_{ \text{ 価数 }} \\
↔︎ x=0.10(mol/L)
\]

関連：計算ドリル、作りました。

化学のグルメオリジナル計算問題集「理論化学ドリルシリーズ」を作成しました！

モル計算や濃度計算、反応速度計算など入試頻出の計算問題を一通りマスターできるシリーズとなっています。詳細は【公式】理論化学ドリルシリーズにて！


著者プロフィール

・化学のグルメ運営代表
・高校化学講師
・薬剤師
・デザイナー/イラストレーター

数百名の個別指導経験あり（過去生徒合格実績：東京大・京都大・東工大・東北大・筑波大・千葉大・早稲田大・慶應義塾大・東京理科大・上智大・明治大など）
2014年よりwebメディア『化学のグルメ』を運営
公式オンラインストアで販売中の理論化学ドリルシリーズ・有機化学ドリル等を執筆

著者紹介詳細