【プロ講師解説】このページでは『酸化還元滴定の一種であるヨウ素滴定（ヨードメトリー・ヨージメトリーそれぞれの原理から入試頻出の計算問題の解法など）』について解説しています。解説は高校化学・化学基礎を扱うウェブメディア『化学のグルメ』を通じて6年間大学受験に携わるプロの化学講師が執筆します。
ヨウ素滴定とは
酸化剤であるヨウ素I2や、還元剤であるヨウ化物イオンI–を使った酸化還元滴定をヨウ素滴定という。（酸化剤・還元剤について詳しくは酸化剤・還元剤（違い・見分け方・例・一覧など）を参照）
ヨウ素滴定にはヨードメトリー（ヨウ素還元滴定）とヨージメトリー（ヨウ素酸化滴定）の2種類が存在する。
ヨードメトリー
還元剤として作用するヨウ化物イオンI–に対して、ある酸化剤を作用させるとヨウ素I2が遊離する。
2I^{-}→I_{2}+2e^{-}
\]
このときI2を、デンプンを指示薬として用い、還元剤であるチオ硫酸ナトリウムNa2S2O3の標準溶液で測定すると、濃度不明の酸化剤を間接的に定量することができる。この方法をヨードメトリー（ヨウ素還元滴定）という。
以下でヨードメトリーの原理（流れ）・ヨードメトリー絡みの計算問題の解法を図付きで解説していく。
ヨードメトリーの原理
ここに、還元剤であるヨウ化カリウムKIが入った容器があるとする。
この容器に、濃度未知の酸化剤である過酸化水素H2O2を加える。
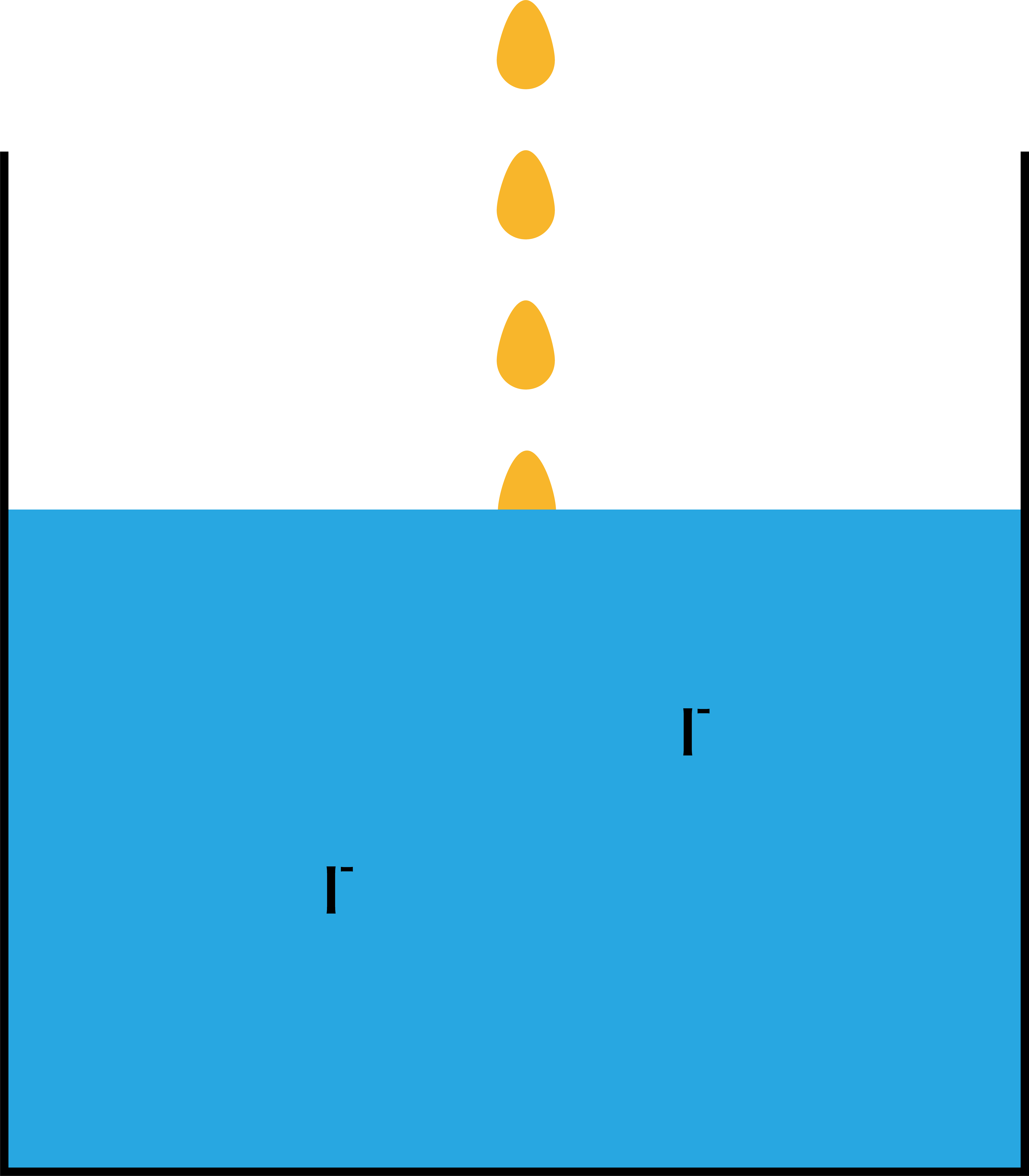
すると、酸化還元反応が起き、H2O2と反応したI–が酸化されてI2となる。
ここに指示薬としてデンプンを加える。
デンプンはI2と反応して青紫色となる（ヨウ素デンプン反応）ため、この時点で容器内は青紫色となる。（ヨウ素デンプン反応について詳しくはヨウ素デンプン反応（原理・色の違い・反応式など）を参照）
最後に、還元剤であるチオ硫酸ナトリウムNa2S2O3水溶液を加えていく。
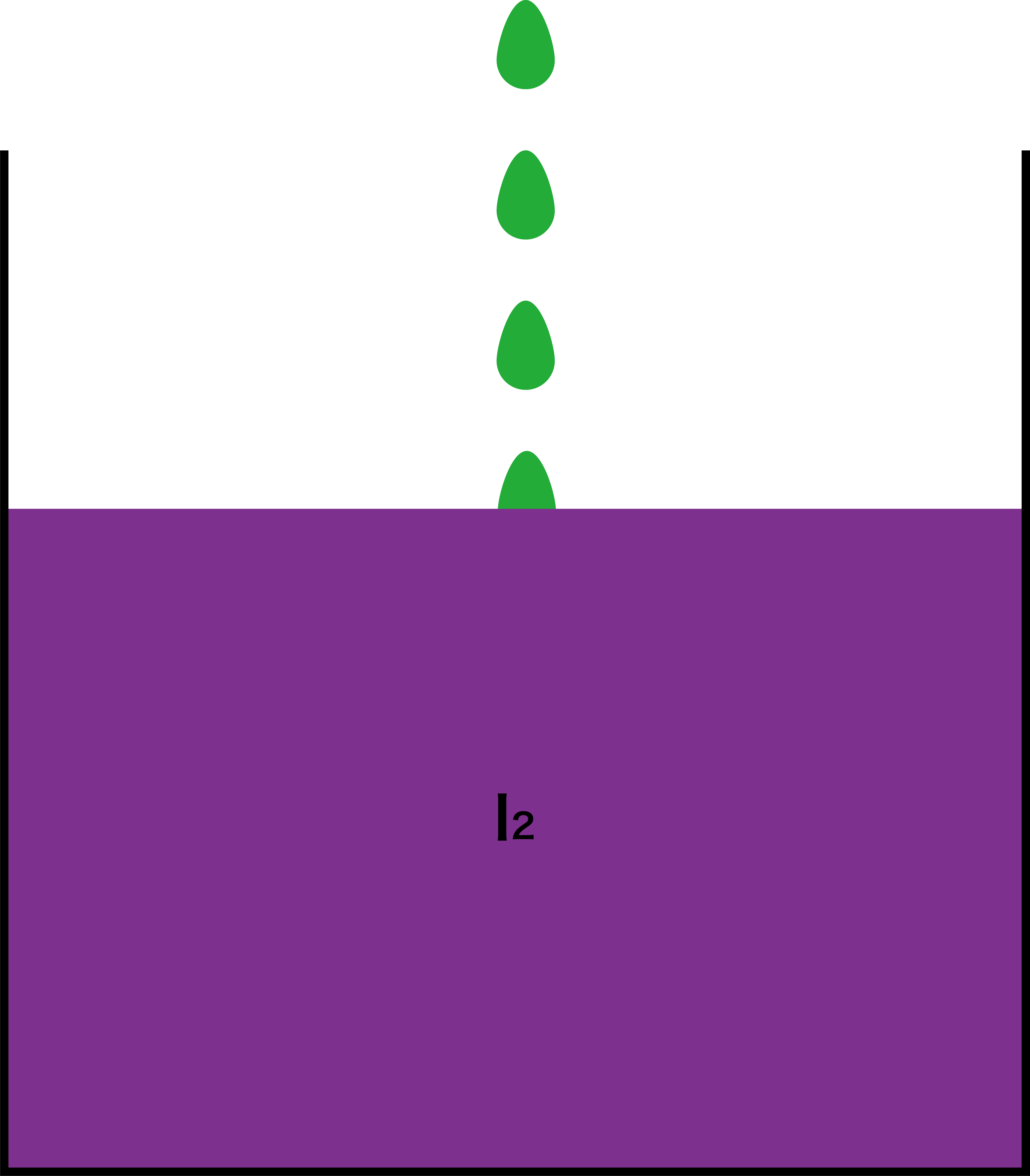
I2が還元されて再びI–となる。
I2が無くなったので、溶液の青紫色は消える。
これがヨードメトリーの流れである。
ヨードメトリーでは、滴下したチオ硫酸ナトリウムNa2S2O3水溶液の量を使って、濃度未知の酸化剤（過酸化水素H2O2等）の濃度を求めていく。
それでは、例題を用いて実際に濃度を求める計算をしていこう。
ヨードメトリーの計算問題の解き方
問題
| STEP1 | ヨウ化カリウムKIと酸化剤（濃度未知）の半反応式から１つの反応式を作る |
| STEP2 | ヨウ素I2とチオ硫酸ナトリウムNa2S2O3の半反応式から、１つの反応式を作る |
| STEP3 | STEP1とSTEP2で作成した式の係数比を利用し、一気に解く |
STEP1
今回は、ヨウ化カリウムKIと濃度未知の過酸化水素H2O2の半反応式を使って、酸化還元反応式を作っていく。
STEP2
STEP3
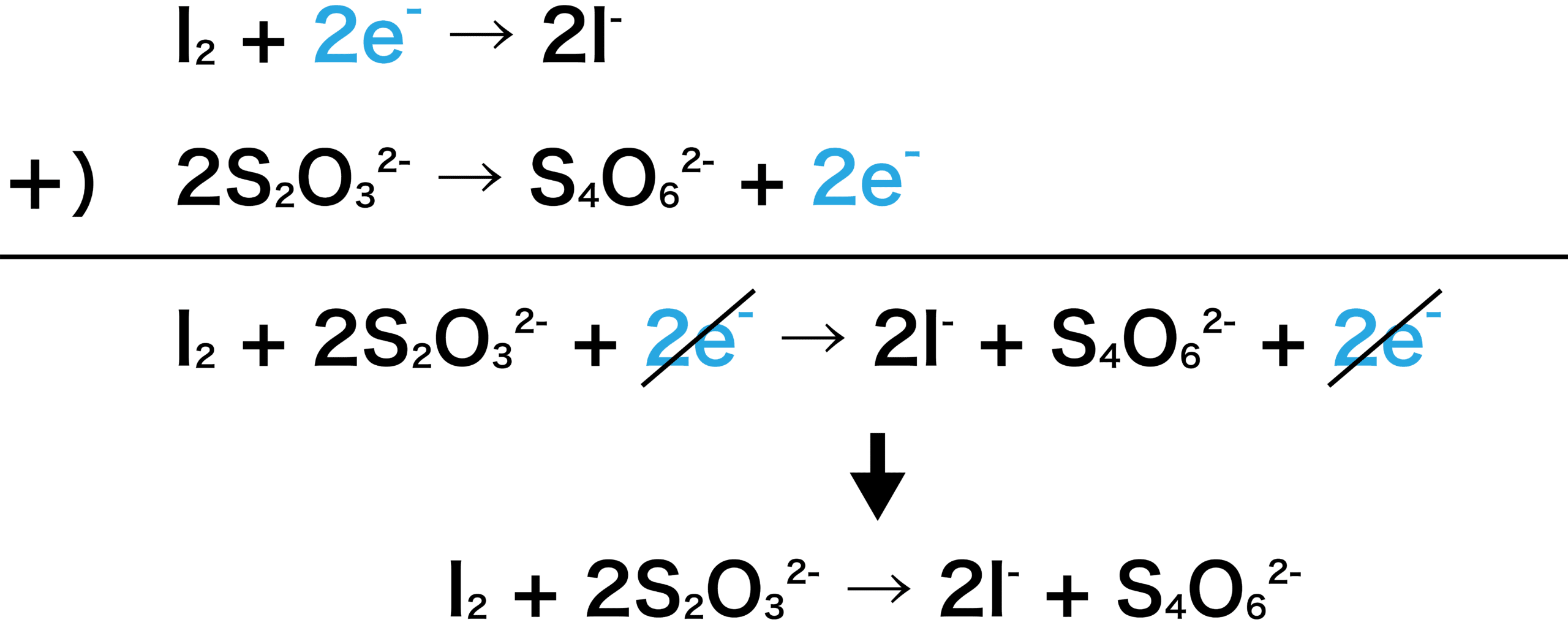
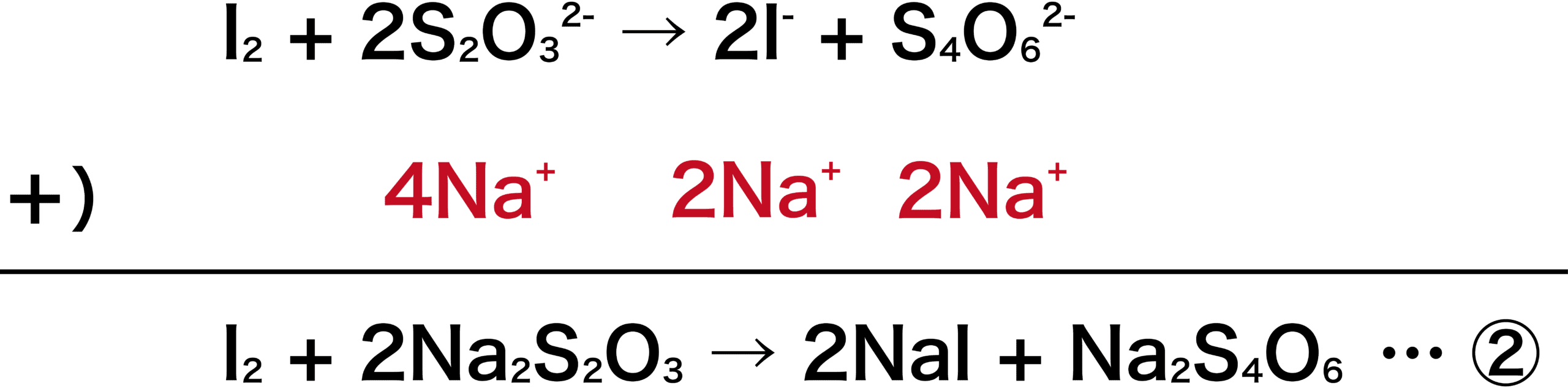
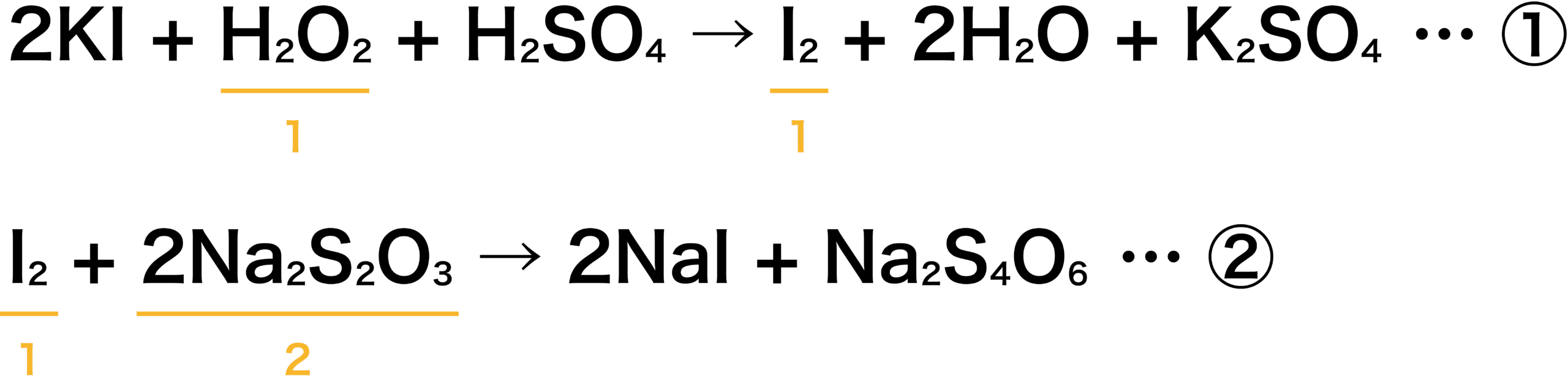
①式よりH2O2とI2は1:1で反応する。
また、②式よりI2とNa2S2O3は1:2で反応する。
よって、H2O2とNa2S2O3は1:2の関係になっている。
ここで、問題文で与えられている数値を用いると、Na2S2O3のmolは次のように求めることができる。
\mathrm{ \begin{align} Na_{2}S_{2}O_{3} &= 1.0(mol/L)×\frac{ 100 }{ 1000 }(L) \\
&=0.10(mol) \end{align} }
\]
したがって…
\mathrm{ H_{2}O_{2}:Na_{2}S_{2}O_{3}=1:2 \\
↔︎ x:0.10=1:2 \\
↔︎ x=0.050(mol) }
\]
問題文より、H2O2は200(mL)あったので、モル濃度は…
\mathrm{ \frac{ 0.050(mol) }{ \frac{ 200 }{ 1000 }(L) }=0.25(mol/L) }
\]
ヨージメトリー
温和な酸化剤であるヨウ素I2の酸化力を利用して、濃度未知の還元剤を直接滴定する方法をヨージメトリー（ヨウ素酸化滴定）という。
以下でヨージメトリーの原理（流れ）・ヨージメトリー絡みの計算問題の解法を図付きで解説していく。
ヨージメトリーの原理
ここに、酸化剤であるヨウ素I2が入った容器があるとする。
この容器に、還元剤である硫化水素H2Sを吸収させる。
H2Sにより還元されたI2はI–となる。
全てのI2がI–となるわけではないので、溶液内にはI2とI–が混在している。
ここに、指示薬としてデンプンを加える。デンプンはI2と反応して青紫色になる（ヨウ素デンプン反応）ため、この時点で容器内は青紫色となる。（ヨウ素デンプン反応について詳しくはヨウ素デンプン反応（原理・色の違い・反応式など）を参照）
最後に、還元剤であるチオ硫酸ナトリウムNa2S2O3を加えていく。
残っていたI2がNa2S2O3により還元され、I–となる。
I2が無くなったので、溶液の青紫色は消える。
以上がヨージメトリーの実験の流れである。
ヨージメトリーでは、滴下したチオ硫酸ナトリウムNa2S2O3水溶液の量を使って、濃度未知の還元剤（硫化水素H2S等）の濃度を求めていく。
それでは、例題を使って実際に濃度を求める計算をしていこう。
ヨージメトリーの計算問題の解き方
問題
| STEP1 | 各物質について半反応式を書く |
| STEP2 | 係数に注意しながら線分図を使って解く |
STEP1
まずは、各物質の半反応式を書く。
今回使われているのは、I2とH2SとNa2S2O3の３つなので、それらの半反応式を書いていく。
\mathrm{ I_{2} + 2e^{-} → 2I^{-} \\
H_{2}S → S + 2H^{+} + 2e^{-} \\
2S_{2}O_{3}^{2-} → S_{4}O_{6}^{2-} + 2e^{-} }
\]
STEP2
今回の問題では、I2という１つの酸化剤をH2S、Na2S2O3という２つの還元剤と反応させている。
それぞれの物質の情報を線分図にすると次のようになる。
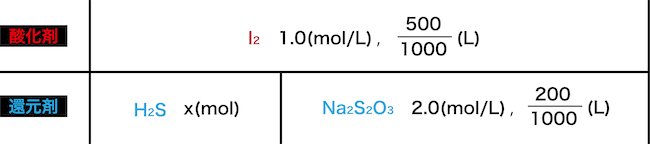
酸化剤の放出するe–の合計と還元剤の放出するe–の合計の(mol)が等しいことから次のような式を作る。
これを解いて…
\mathrm{ x=0.30(mol) }
\]
この式について理解できなければ酸化還元滴定（実験・計算問題・指示薬・硫酸酸性にする理由など）を参照しよう。
関連：計算ドリル、作りました。
化学のグルメオリジナル計算問題集「理論化学ドリルシリーズ」を作成しました！モル計算や濃度計算、反応速度計算など入試頻出の計算問題を一通りマスターできるシリーズとなっています。詳細は【公式】理論化学ドリルシリーズにて！
・化学のグルメ運営代表
・高校化学講師
・薬剤師
・デザイナー/イラストレーター
数百名の個別指導経験あり（過去生徒合格実績：東京大・京都大・東工大・東北大・筑波大・千葉大・早稲田大・慶應義塾大・東京理科大・上智大・明治大など）
2014年よりwebメディア『化学のグルメ』を運営
公式オンラインストアで販売中の理論化学ドリルシリーズ・有機化学ドリル等を執筆
著者紹介詳細