気体の溶解度（ヘンリーの法則・体積や圧力との関係・計算問題）

2018年5月2日2023年6月23日

はじめに

【プロ講師解説】このページでは『気体の溶解度（ヘンリーの法則・体積や圧力との関係・計算問題）』について解説しています。

気体の溶解度

温度が高く圧力が小さいほど、気体の溶解度は小さくなる。

温度(高) ・圧力(小) → 溶解度(小)

ヘンリーの法則

温度が一定のとき、気体の溶解度はその気体の圧力に比例する。これをヘンリーの法則という。

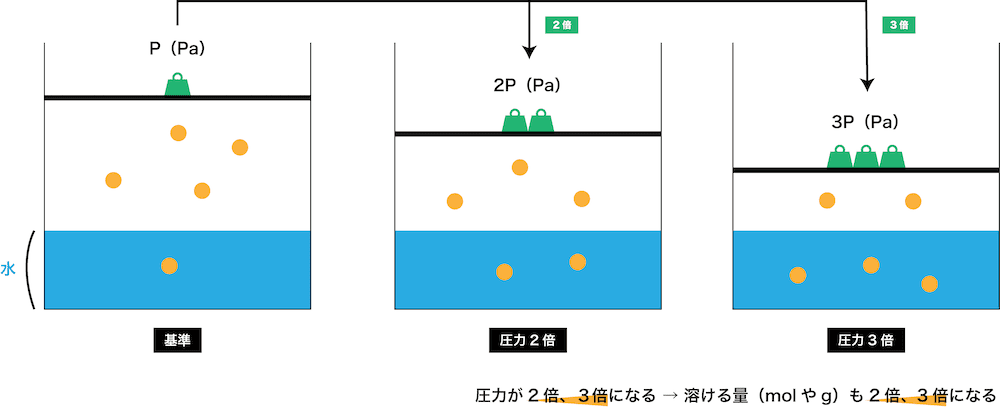
ヘンリーの法則は、水への溶解度が小さい（＝水との反応性が小さい）気体において成立する。（アンモニアNH₃や塩化水素HClなど、水に溶けやすい気体には適用不可）

気体の溶解度計算（ヘンリーの法則を使った計算）

ヘンリーの法則を用いた気体の溶解度計算について、「1種類の気体を溶解させるパターン」と「2種類の気体を溶解させるパターン」に分けて解説する。

1種類の気体を溶解させるパターン

問題

0℃で酸素の圧力を2.0×10⁵Paにした。このとき2.0Lの水に溶ける酸素は何Lか。ただし、酸素は0℃、1.0×10⁵Paにおいて、水1.0Lに4.9×10^ー2L溶けるものとする。

ヘンリーの法則より、気体の溶ける量は圧力に比例する。また、当然水量にも比例する。
したがって、この問題は次のような式を使って解くことができる。

基準の量 × 圧力比 × 水量比

\[ \begin{align}&4.9×10^{-2}(\mathrm{L})×\color{#3ADF00}{ \frac{ 2.0×10^{5}(\mathrm{Pa}) }{ 1.0×10^{5}(\mathrm{Pa}) }}× \color{#01DFD7}{\frac{ 2.0(\mathrm{L}) }{ 1.0(\mathrm{L}) }}\\
&≒0.20(\mathrm{L})\end{align} \]

2種類の気体を溶解させるパターン

問題

酸素と窒素が1：4の体積比で混合した標準状態（0℃、1.0×10⁵Pa）の空気がある。
このとき、次の問いに答えなさい。
ただし、0℃、1.0×10⁵Paのもとで1.0Lの水に窒素は23mL、酸素は49mL溶けるものとする。

（１）この空気と接している水2.0Lに溶解している窒素の体積(mL)を求めよ。
（２）この空気と接している水3.0Lに溶解している酸素の物質量(mol)を求めよ。
（３）この空気と接している水10Lに溶解している窒素と酸素の質量比（N₂/O₂）を求めよ。

（１）

分圧・全圧・モル分率にある「分圧＝全圧×モル分率」の公式より、窒素の分圧は次のようになる。

\[ 1.0×10^{5}×\frac{ 4 }{ 5 } \]

これを用いて、次のような式をたてることができる。

\[ \begin{align}&23(\mathrm{mL})×\color{#3ADF00}{ \frac{ 1.0×10^{5}(\mathrm{Pa})×\frac{ 4 }{ 5 } }{ 1.0×10^{5}(\mathrm{Pa}) }}× \color{#01DFD7}{\frac{ 2.0(\mathrm{L}) }{ 1.0(\mathrm{L}) }}\\
&≒37(\mathrm{mL}) \end{align}\]

（２）

酸素の分圧を上と同様に求めると、次のようになる。

\[ 1.0×10^{5}×\frac{ 1 }{ 5 } \]

これを用いて、次のような式をたてることができる。

\[ \begin{align}&\frac{ 49(\mathrm{mL})×\color{#3ADF00}{ \frac{ 1.0×10^{5}(\mathrm{Pa})×\frac{ 1 }{ 5 } }{ 1.0×10^{5}(\mathrm{Pa}) }}× \color{#01DFD7}{\frac{ 3.0(\mathrm{L}) }{ 1.0(\mathrm{L}) }}}{ 22400(\mathrm{mL/mol}) }\\
&≒1.3×10^{-3}(\mathrm{mol}) \end{align}\]

（３）

分母がO₂のg、分子がN₂のgになるように単位を揃えて約分すれば良い。

\[ \begin{align}&\frac{w_{N_{2}}(\mathrm{g})}{w_{O_{2}}(\mathrm{g})}\\
&=\frac{
\frac{ 23(\mathrm{mL})×\color{#3ADF00}{ \frac{ 1.0×10^{5}(\mathrm{Pa})×\frac{ 4 }{ 5 } }{ 1.0×10^{5}(\mathrm{Pa}) }}× \color{#01DFD7}{\frac{ 10(\mathrm{L}) }{ 1.0(\mathrm{L}) }}}{ 22400(\mathrm{mL/mol}) }×28(\mathrm{g/mol}) }
{
\frac{ 49(\mathrm{mL})×\color{#3ADF00}{ \frac{ 1.0×10^{5}(\mathrm{Pa})×\frac{ 1 }{ 5 } }{ 1.0×10^{5}(\mathrm{Pa}) }}× \color{#01DFD7}{\frac{ 10(\mathrm{L}) }{ 1.0(\mathrm{L}) }}}{ 22400(\mathrm{mL/mol}) }×32(\mathrm{g/mol}) }\\
&≒1.6\end{align} \]