【モル計算】単位を駆使！物質量molが絡む問題の解法（原子量・体積・アボガドロ数など）

はじめに

【プロ講師解説】このページでは『【モル計算】単位を駆使！物質量molが絡む問題の解法（原子量・体積・アボガドロ数など）』について解説しています。

物質量（mol）とは

• 物質量は「単位」の1つである。つまり、「長さ」や「重さ」と同じ類のものだということ。「長さ」を「m」、重さを「g」で表すように、物質量は「mol」で表す。
• 鉛筆を12本集めたものを…1″ダース”という。

• これと同様の考え方で、粒子（原子・分子など）を6.0×10²³個集めたカタマリを…1″mol”という。

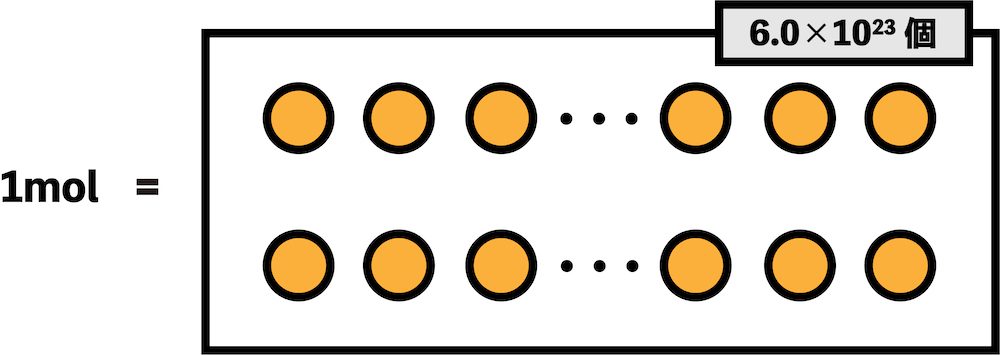
• ちなみに、6.0×10²³個という数はどんな粒子でも同じである。

以上が物質量（mol）に関する簡単な説明です。特別なものではなく、単位の一種に過ぎないということが理解できれば問題ありません。これ以降、物質量に関連した単位をいくつか紹介した後、具体的なモル計算問題の解法について説明していきます。

アボガドロ定数（個数に関係したもの）

• 6.0×10²³個は1molに含まれる粒子の個数である。
• 単位をつけると6.0×10²³個/molとなり、これをアボガドロ定数という。
• アボガドロ定数は記号N_Aで表す。

\[ \mathrm{アボガドロ定数N_{A}＝6.0×10^{23} (個/mol) } \]

※ここではイメージしやすくするために単位に「個」をつけているが、本来アボガドロ定数の単位は「/mol」である。計算をするときは「個/mol」で覚えていた方が扱いやすいが、一応把握しておこう。
※molの前に省略されている「1」を補うとさらにイメージしやすいかも。

\[ \mathrm{6.0×10^{23} (個/1mol)} \]

モル質量（質量に関係したもの）

• 粒子1molあたりの質量をモル質量という。
• モル質量は原子量（分子量・式量）と一致し、単位「g/mol」をつけて表す。

\[ \mathrm{モル質量(g/mol)} \]

モル体積（体積に関係したもの）

• 全ての気体は「標準状態（0℃、1気圧）で1molあたり22.4Lの体積を占める」ことが知られている。
• 「1molあたりのL」を単位で表すと「L/mol」となるので、「1molあたり22.4Lの体積を占める」というのを単位をつけて表すと、「22.4(L/mol)」となる。

\[ \mathrm{22.4(L/mol)} \]

気体の密度と分子量

• 気体の密度は通常1Lあたりの質量(g/L)で表す。
• これに22.4(L/mol)をかけると、22.4Lあたりの質量、つまり、1molあたりの質量（モル質量）になる。

\[ \mathrm{気体の密度(g/L) × 22.4(L/mol) = モル質量(g/mol)} \]

molとgの計算

• molとgに関する計算をするときにポイントとなるのは「モル質量」である。
• 先述の通り、モル質量は原子量（分子量・式量）の値と一致し、単位はg/molである。

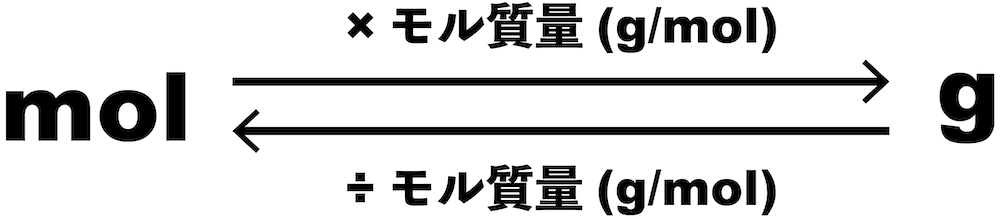
mol→g

• molからgを求めるときは、molにモル質量(g/mol)をかける。
• すると、molが約分され、gを得ることができる。

\[ \mathrm{\cancel{mol} \times \frac{ g }{ \cancel{mol} } = g} \]

• molとモル質量がわかっているので、これらをかけあわせる。

\[ \mathrm{2.0(\cancel{mol}) \times 18(g/\cancel{mol}) = 36(g)} \]

g→mol

• gからmolを求めるときは、gをモル質量(g/mol)で割る。
• すると、gが約分され、molを求めることができる。

\[ \begin{align}
&\mathrm{g \div \frac{ g }{ mol }} \\
&\mathrm{= \cancel{g} \times \frac{ mol }{ \cancel{g} }} \\
&\mathrm{= mol}
\end{align} \]

• gをモル質量(g/mol)で割ると、

\[ \begin{align}
&\mathrm{44(g) \div 44(g/mol) }\\
&\mathrm{= 44(\cancel{ g }) \times \frac{ 1 }{ 44 }(mol/\cancel{ g })} \\
&\mathrm{= 1.0(mol)}
\end{align} \]

molとLの計算

• 先述の通り、標準状態（０℃・１気圧）で、すべての気体は1molあたり22.4Lの体積を占める。これがmolとLに関する計算をするときのポイントである。

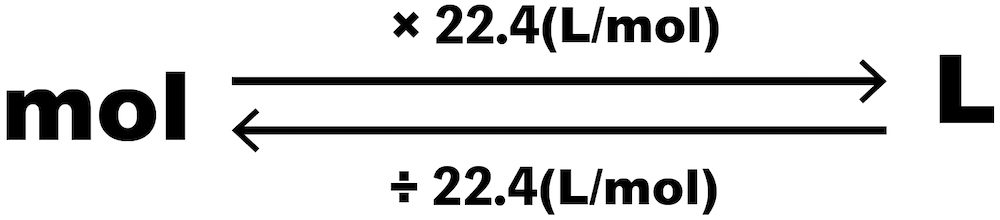
mol→L

• molからLを求めるときは、molに22.4(L/mol)をかける。
• すると、molが約分され、Lを得ることができる。

\[ \mathrm{\cancel{mol} \times \frac{ L }{ \cancel{mol} } = L} \]

• 標準状態でmolがわかっているので…

\[ \mathrm{0.50(\cancel{mol}) \times 22.4(L/\cancel{mol}) = 11.2(L)} \]

L→mol

• Lからmolを求めるときは、Lを22.4(L/mol)で割る。
• すると、Lが約分され、molを求めることができる。

\[ \begin{align}
&\mathrm{L \div \frac{ L }{ mol } } \\
&\mathrm{= \cancel{L} \times \frac{ mol }{ \cancel{L} } }\\
&\mathrm{= mol}
\end{align} \]

• Lを22.4(L/mol)で割ると…

\[ \begin{align}
&\mathrm{2.24(L) \div 22.4(L/mol)} \\
&\mathrm{= 2.24(\cancel{ L }) \times \frac{ 1 }{ 22.4 }(mol/\cancel{ L })} \\
&\mathrm{= 0.10(mol)}
\end{align} \]

molと個数の計算

• 先述の通り、1molには6.0×10²³個の粒子が含まれる。これがmolと個数に関する計算をするときのポイントである。

mol→個数

• molから個数を求めるときは、molに6.0×10²³(個/mol)をかける。
• すると、molが約分され、個数を得ることができる。

\[ \mathrm{\cancel{mol} \times \frac{ 個 }{ \cancel{mol} } = 個} \]

• 個数がわかっているため…

\[ \mathrm{0.50(\cancel{mol}) \times 6.0×10^{23}(個/\cancel{mol}) = 3.0×10^{23}(個)} \]

個数→mol

• 個数からmolを求めるときは、個数を6.0×10²³(個/mol)で割る。
• すると、個数が約分され、molを求めることができる。

\[ \begin{align}
&\mathrm{個 \div \frac{ 個 }{ mol } } \\
&\mathrm{= \cancel{個} \times \frac{ mol }{ \cancel{個} } }\\
&\mathrm{= mol}
\end{align} \]

• 個数を6.0×10²³(個/mol)で割ると…

\[ \begin{align}
&\mathrm{1.2×10^{23}(個) \div 6.0×10^{23}(個/mol) }\\
&\mathrm{= 1.2×10^{23}(\cancel{ 個 }) \times \frac{ 1 }{ 6.0×10^{23} }(mol/\cancel{ 個 }) }\\
&\mathrm{= 0.20(mol)}
\end{align} \]

gとLの変換

• ここからは、molを利用した応用的な単位変換計算を紹介する。
• まずは、gとLの変換である。

g→L

• g→Lの変換は「gをmolに変換し、そのmolをLに変換する」という方法で行う。

• まずは、gをモル質量(g/mol)で割ることで、molを求める。

\[ \begin{align}
&\mathrm{3.2(g) \div 32(g/mol)} \\
&\mathrm{= 3.2(\cancel{ g }) \times \frac{ 1 }{ 32 }(mol/\cancel{ g }) }\\
&\mathrm{= 0.10(mol) }
\end{align}\]

• 次に、今求めたmolに22.4(L/mol)をかけることで、Lを求める。

\[ \mathrm{0.100(\cancel{mol}) \times 22.4(L/\cancel{mol}) = 2.24(L) }\]

L→g

• L→gの変換は「Lをmolに変換し、そのmolをgに変換する」という方法で行う。

• まずは、Lを22.4(L/mol)で割ることで、molを求める。

\[ \begin{align}
&\mathrm{11.2(L) \div 22.4(L/mol)} \\
&\mathrm{= 11.2(\cancel{ L }) \times \frac{ 1 }{ 22.4 }(mol/\cancel{ L }) }\\
&\mathrm{= 0.500(mol)}
\end{align} \]

• 次に、今求めたmolにモル質量(g/mol)をかけることで、gを求める。

\[ \mathrm{0.500(\cancel{mol}) \times 2(g/\cancel{mol}) = 1.0(g)} \]

gと個数の変換

• 次はgと個数の変換である。

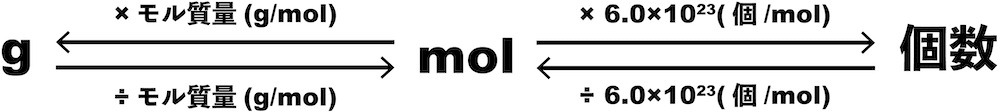
g→個数

• g→個数の変換は「gをmolに変換し、そのmolを個数に変換する」という方法で行う。

• まずは、gをモル質量(g/mol)で割ることで、molを求める。

\[ \begin{align}
&\mathrm{8.8(g) \div 44(g/mol)} \\
&\mathrm{= 8.8(\cancel{ g }) \times \frac{ 1 }{ 44 }(mol/\cancel{ g }) }\\
&\mathrm{= 0.20(mol) }
\end{align}\]

• 次に、今求めたmolに6.0×10²³(個/mol)をかけることで、個数を求める。

\[ \mathrm{0.20(\cancel{mol}) \times 6.0×10^{23}(個/\cancel{mol}) = 1.2×10^{23}(個)} \]

個数→g

• 個数→gの変換は「個数をmolに変換し、そのmolをgに変換する」という方法で行う。

• まずは、個数を6.0×10²³(個/mol)で割ることで、molを求める。

\[ \begin{align}
&\mathrm{3.0×10^{23}(個) \div 6.0×10^{23}(個/mol)} \\
&\mathrm{= 3.0×10^{23}(\cancel{ 個 }) \times \frac{ 1 }{ 6.0×10^{23} }(mol/\cancel{ 個 }) }\\
&\mathrm{= 0.50(mol)}
\end{align} \]

• 次に、今求めたmolにモル質量(g/mol)をかけることで、gを求める。

\[ \mathrm{0.50(\cancel{mol}) \times 28(g/\cancel{mol}) = 14(g) }\]

Lと個数の変換

• 最後は、Lと個数の変換である。

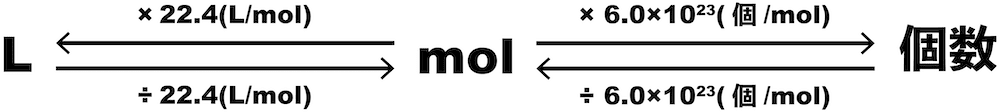
L→個数

• L→個数の変換は「Lをmolに変換し、そのmolを個数に変換する」という方法で行う。

• まずは、Lを22.4(L/mol)で割ることで、molを求める。

\[ \begin{align}
&\mathrm{4.48(L) \div 22.4(L/mol)} \\
&\mathrm{= 4.48(\cancel{ L }) \times \frac{ 1 }{ 22.4 }(mol/\cancel{ L }) }\\
&\mathrm{= 0.20(mol) }
\end{align}\]

• 次に、今求めたmolに6.0×10²³(個/mol)をかけることで、個数を求める。

\[ \mathrm{0.20(\cancel{mol}) \times 6.0×10^{23}(個/\cancel{mol}) = 1.2×10^{23}(個) }\]

個数→L

• 個数→Lの変換は「個数をmolに変換し、そのmolをLに変換する」という方法で行う。

• まずは、個数を6.0×10²³(個/mol)で割ることで、molを求める。

\[ \begin{align}
&\mathrm{1.2×10^{24}(個) \div 6.0×10^{23}(個/mol) }\\
&\mathrm{= 1.2×10^{24}(\cancel{ 個 }) \times \frac{ 1 }{ 6.0×10^{23} }(mol/\cancel{ 個 }) }\\
&\mathrm{= 2.0(mol)}
\end{align} \]

• 次に、今求めたmolに22.4(L/mol)をかけることで、Lを求める。

\[ \mathrm{2.0(\cancel{mol}) \times 22.4(L/\cancel{mol}) = 44.8(L)} \]