分圧・全圧・モル分率

【プロ講師解説】このページでは『分圧・全圧・モル分率』について解説しています。解説は高校化学・化学基礎を扱うウェブメディア『化学のグルメ』を通じて6年間大学受験に携わるプロの化学講師が執筆します。

分圧・全圧とは

気体Aと気体Bの混合気体を体積Vと温度Tを一定のまま、成分ごとに分けたとする。

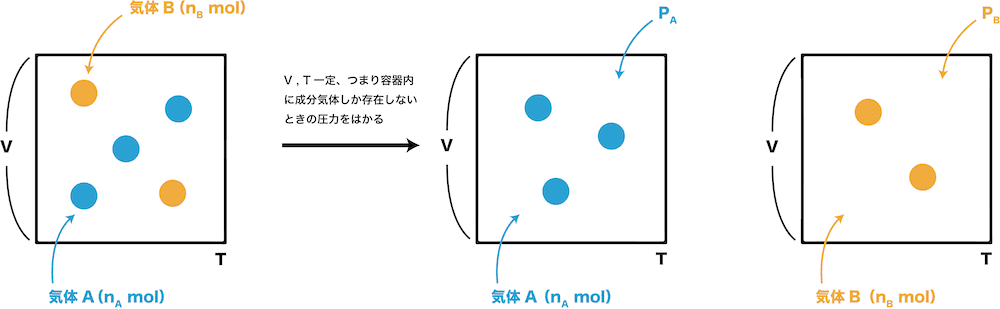
このとき、気体Aの圧力（P_A）、気体Bの圧力（P_B）を分圧という。

それぞれの分圧は気体の状態方程式PV=nRTを使って次のように表すことができる。

\[
P_{A}=\frac{ RT }{ V }・n_{A}・・・①
\]

\[
P_{B}=\frac{ RT }{ V }・n_{B}・・・②
\]

また、気体Aと気体Bを合わせた、混合気体の圧力を全圧（P_全）という。

\[
P_{全}=\frac{ RT }{ V }(n_{A}+n_{B})・・・③
\]

分圧と全圧の関係

体積Vと温度Tが一定のとき、上の①〜③式中のRT/Vは一定なのでCと置く。すると、①〜③式は次のように書くことができる。

\[
P_{A}=C・n_{A}・・・④ \\
P_{B}=C・n_{B}・・・⑤ \\
P_{全}=C(n_{A}+n_{B})・・・⑥
\]

④〜⑥式より、全圧と分圧の関係は次のように表すことができる。

\[
P_{全}=P_{A}+P_{B}
\]

この関係はドルトンの分圧の法則と呼ばれる。

モル分率

Point!

混合気体の物質量に対する特定の気体の物質量の割合をモル分率という。

全圧にモル分率をかけることで、その気体の分圧を求めることができる。

\[
P_{A}=P_{全}×\frac{ n_{A} }{ n_{A}+n_{B} }
\]

※上式の導出

\[
P_{A}=C・n_{A}・・・④ \\
P_{B}=C・n_{B}・・・⑤ \\
P_{全}=C(n_{A}+n_{B})・・・⑥
\]

④〜⑥式より、Pが２倍になればnも２倍に、Pが半分になればnも半分になる。つまり、「圧力比＝モル比」が成り立っている。

このとき、混合気体と気体A、混合気体と気体Bの圧力とモル数の関係は…

\[
P_{全}:P_{A}=n_{A}+n_{B}:n_{A} \\
P_{全}:P_{B}=n_{A}+n_{B}:n_{B}
\]

このようになる。よって…

\[
P_{A}=P_{全}×\frac{ n_{A} }{ n_{A}+n_{B} }\\
P_{B}=P_{全}×\frac{ n_{B} }{ n_{A}+n_{B} }
\]

演習問題

問１

【】に当てはまる用語を答えよ。

気体Aと気体Bの混合気体を体積Vと温度Tを一定のまま、成分ごとに分けたとする。

このとき、気体Aの圧力（P_A）、気体Bの圧力（P_B）を【１】という。

また、気体Aと気体Bを合わせた、混合気体の圧力を【２】（P_全）という。

【問１】解答/解説：タップで表示

解答：【１】分圧【２】全圧

気体Aと気体Bの混合気体を体積Vと温度Tを一定のまま、成分ごとに分けたとする。

このとき、気体Aの圧力（P_A）、気体Bの圧力（P_B）を分圧という。

それぞれの分圧は気体の状態方程式PV=nRTを使って次のように表すことができる。

\[
P_{A}=\frac{ RT }{ V }・n_{A}・・・①
\]

\[
P_{B}=\frac{ RT }{ V }・n_{B}・・・②
\]

また、気体Aと気体Bを合わせた、混合気体の圧力を全圧（P_全）という。

\[
P_{全}=\frac{ RT }{ V }(n_{A}+n_{B})・・・③
\]

問２

【】に当てはまる用語を答えよ。

混合気体のmol数に対する特定の気体のmol数の割合を【１】という。

【問２】解答/解説：タップで表示

解答：【１】モル分率

混合気体の物質量に対する特定の気体の物質量の割合をモル分率という。

問３

体積が一定の容器に、一定温度で0.30molの水素H₂と0.60molの酸素O₂を入れたところ、容器内の気体の圧力は6.0×10⁵Paとなった。このときのH₂とO₂の分圧をそれぞれ求めよ。

【問３】解答/解説：タップで表示

解答：P_H₂：2.0×10⁵Pa　P_O₂：4.0×10⁵Pa

先ほどの公式を使おう。

\[
P_{A}=P_{全}×\frac{ n_{A} }{ n_{A}+n_{B} }
\]

まずは水素の分圧P_H₂を求める。

\[
\begin{align} P_{H_{2}}&=P_{全}×\frac{ n_{H_{2}} }{ n_{H_{2}}+n_{O_{2}} }\\
&=6.0×10^{5}×\frac{ 0.30 }{ 0.30+0.60 }\\
&=2.0×10^{5}(Pa)\end{align}
\]

次に酸素の分圧P_O₂を求める。

\[
\begin{align}P_{O_{2}}&=P_{全}×\frac{ n_{O_{2}} }{ n_{H_{2}}+n_{O_{2}} }\\
&=6.0×10^{5}×\frac{ 0.60 }{ 0.30+0.60 }\\
&=4.0×10^{5}(Pa)\end{align}
\]

問４

体積8.3Lの容器に0.20molの水素H₂と0.30molの窒素N₂を入れて27℃にした。このときの混合気体の全圧、またH₂とN₂の分圧をそれぞれ求めよ。（気体定数R=8.3×10³とする）

【問４】解答/解説：タップで表示

解答：P_全：1.5×10⁵Pa　P_H₂：6.0×10⁴Pa　P_N₂：9.0×10⁴Pa

まずは、気体の状態方程式を使って全圧を求める。

\[
\begin{align} PV&=nRT\\
P&=\frac{ nRT }{ V }\\
&=\frac{ 0.50×8.3×10^{3}×(27+273) }{ 8.3 }\\
&=1.5×10^{5}(Pa) \end{align}
\]

次に、全圧にH₂とN₂それぞれのモル分率をかけることで分圧を求める。

\[
\begin{align}P_{H_{2}}&=P_{全}×\frac{ n_{H_{2}} }{ n_{H_{2}}+n_{N_{2}} }\\
&=1.5×10^{5}×\frac{ 0.20 }{ 0.20+0.30 }\\
&=6.0×10^{4}(Pa) \end{align}
\]

\[
\begin{align}P_{N_{2}}&=P_{全}×\frac{ n_{N_{2}} }{ n_{H_{2}}+n_{N_{2}} }\\
&=1.5×10^{5}×\frac{ 0.30 }{ 0.20+0.30 }\\
&=9.0×10^{4}(Pa) \end{align}
\]

※気体の状態方程式について詳しくは気体の状態方程式（単位・導出・計算問題の解き方など）を参照

分圧・全圧とは

分圧と全圧の関係

モル分率

演習問題

関連：計算ドリル、作りました。