MENU
反応速度計算(求め方・測定・式・単位の変換など)
はじめに
【プロ講師解説】このページでは『反応速度計算(求め方・測定・式・単位の変換など)』について解説しています。
反応速度と2つの式
- 反応速度計算に関連する公式として「定義式」と「速度式」を紹介する。
●反応速度計算に関連する式
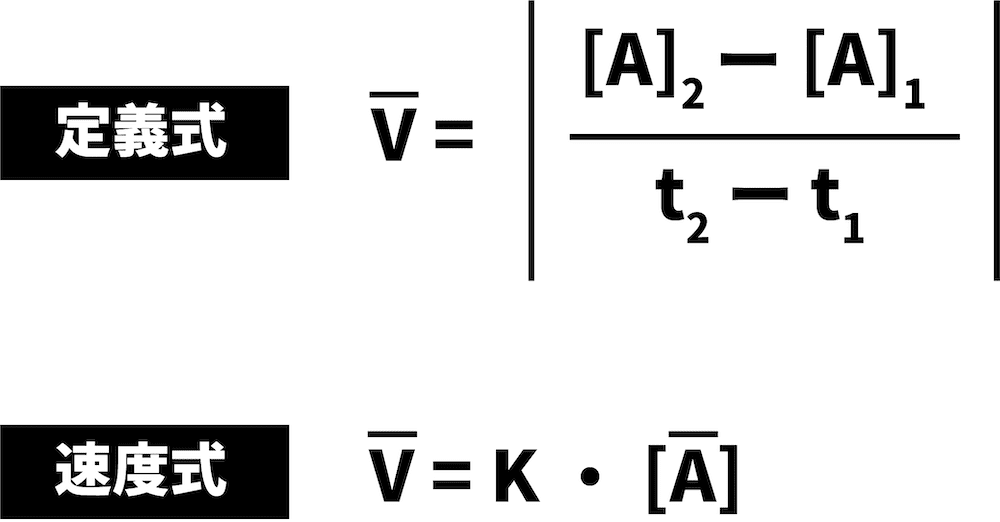
定義式
- 次の化学反応が起こる場合を考える。
\[ \mathrm{A→B+C} \]
- これをグラフにすると、次のようになる。
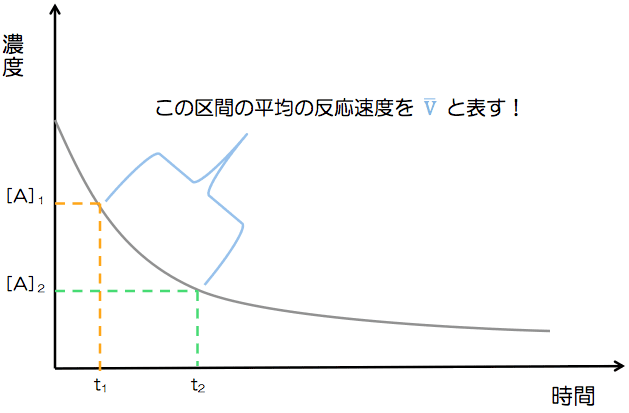
- このとき、青の区間の平均の反応速度は次のように表すことができる。
\[ \overline{ V }=\left|\frac{ [A]_{2}-[A]_{1} }{ t_{2}-t_{1} }\right| \]
- [A]1は時間t1のときの反応物Aの濃度、[A]2は時間t2のときの反応物Aの濃度である。(Aの濃度は減少しているため、分子が負の値になってしまう。速度にマイナスがつくのはおかしいため、絶対値を付けている)
- この式は「反応速度とはこういうものである」として定義されたものなので、定義式とよぶ。
速度式
- 反応速度は、反応速度定数(K)を用いて次のように表すこともできる。
\[ \begin{align}&平均の速度\overline{ V }=K・[\overline{ A }]\\
&瞬間の速度V=K・[A] \end{align}\]
- この反応速度定数(K)を用いた式を速度式(反応速度式)とよび、「平均の速度」と「瞬間(一時点)の速度」のどちらを求めるときにも使うことができる。
- ちなみにAの平均濃度は以下の式によって求めることができる。
\[ [\overline{ A }]=\frac{ [A]_{1}+[A]_{2} }{ 2 } \]
入試頻出の反応速度計算
- 定義式や速度式を使った入試頻出の計算問題の解き方について、次のSTEPを用いて解説する。
●STEP1
定義式を用いて、平均の速さを求める。
\[ \begin{align}
\color{red}{\overline{ V }}&=\left|\frac{ [A]_{2}-[A]_{1} }{ t_{2}-t_{1} }\right|
\end{align} \]
●STEP2
速度式を用いて、反応速度定数(K)を求める。
\[ \overline{ V }=\color{red}{K}・[\overline{ A }] \]
●STEP3
速度式を用いて、瞬間の速さを求める。
\[ \begin{align}
\color{red}{V}&=K・[A]
\end{align} \]
A→2B+Cの反応が起こるとする。一定温度でAの濃度を測定すると下図のようになった。
| t(s) | [A](mol/L) |
|---|---|
| 0 | 6.00 |
| 100 | 4.00 |
(1)0から100秒の平均の速度(mol/(L・s))を求めよ。
(2)反応速度定数(K)の値を求めよ。ただし、単位も明記すること。
(3)実験開始から200秒後のAの濃度は3.50(mol/L)であった。この時点における瞬間の速さ(mol/(L・s))を求めよ。
まずは、定義式を用いて、平均の速さを求める。
\[ \begin{align}
\overline{ V }&=\left|\frac{ [A]_{2}-[A]_{1} }{ t_{2}-t_{1} }\right|\\
\\
&=\left|\frac{ 4.00-6.00 }{ 100-0 }\right|\\
\\
&=2.00×10^{-2}(\mathrm{mol/(L・s)})
\end{align} \]
次に、速度式(平均の速さ)を用いて反応速度定数(K)を求める。
\[ \begin{align}&\overline{ V }=K・[\overline{ A }]\\
&\leftrightarrow 2.00×10^{-2}=K・\frac{ 6.00+4.00 }{ 2 }\\
&\leftrightarrow K=4.00×10^{-3}(\mathrm{/s})\end{align} \]
最後に、速度式(瞬間の速さ)を用いて瞬間の速さを求める。
\[ \begin{align}
V&=K・[A]\\
&=4.00×10^{-3}×3.50\\
&=1.4×10^{-2}(\mathrm{mol/(L・s)})
\end{align} \]
演習問題
化学のグルメでは、高校化学・化学基礎の一問一答問題を公開しています。問題一覧は【スマホで出来る】一問一答(高校化学・化学基礎)でご覧下さい。
化学反応の速さは単位時間あたりの濃度の変化量で表され、これを【1】という。
解答/解説:タップで表示
解答:【1】反応速度
化学反応の速さは単位時間あたりの濃度の変化量で表され、これを反応速度という。
\[ \overline{ V }=\left|\frac{ [A]_{2}-[A]_{1} }{ t_{2}-t_{1} }\right| \]
反応物の濃度と反応速度の関係を表す式を【1】といい、この式に含まれる定数Kを【2】という。
解答/解説:タップで表示
解答:【1】反応速度式【2】反応速度定数
反応速度は、反応速度定数(K)を用いて次のように表すこともできる。
\[ \begin{align}&平均の速度\overline{ V }=K・[\overline{ A }]\\
&瞬間の速度V=K・[A] \end{align}\]
この反応速度定数(K)を用いた式を速度式(反応速度式)とよぶ。
水素とヨウ素を密閉容器に入れ加熱すると、以下の反応が起こる。
\[ K=A・e^{-\frac{ E_{a} }{ RT }} \]
(1)正反応・逆反応の速さ(V1・V2)を、それぞれ式で表せ。ただし、正反応の反応速度定数はK1、逆反応の反応速度定数はK2とする。
(2)この反応において、H2の濃度を2倍、I2の濃度を3倍にすると、正反応の速さは何倍になるか。
(3)この反応において、圧力を元の4倍にしたとすると、正反応の速さは何倍になるか。
解答/解説:タップで表示
解答:(1)『正反応』V1=K1×[H2][I2] 『逆反応』V2=K2×[HI]2(2)6倍(3)16倍
(1)
まずは、正反応と逆反応の違いについて理解しておく必要がある。
\[ \mathrm{H_{2}+I_{2}\underset{逆反応}{\overset{正反応}{\rightleftarrows}}2HI} \]
正反応は左向きの反応、逆反応は右向きの反応である。
参考:可逆反応と不可逆反応
正反応の速度式は、上で説明してきた通り次の式を使う。
\[ V=K・[A] \]
今回は、反応物(上の式のA)がH2とI2の2つなので、次のように表すことができる。
\[ V_{1}=K_{1}×[\mathrm{H_{2}}][\mathrm{I_{2}}] \]
次は、逆反応の速度式を考えていく。
まず逆反応における「反応物」が何かを考える。今回の反応式における逆反応では、HIからH2とI2が生成している。したがって、反応物は「HI」だということになる。(反応のスタート時点の物質=反応物)
正反応と同じように次のような式を導くことができる。
\[ V=K・[A] \]
\[ V_{2}=K_{2}×[\mathrm{HI}]^{2} \]
逆反応では、反応物の濃度([A])のところにはHIの濃度([HI])を当てはめている。
※[HI]が2乗になっているのは、反応式中のHIの係数が「2」だからである。
今回の反応のように、1段階だけで完結する”素反応”であり、かつ反応全体が1つの素反応でできている反応(単純反応)に限り、反応式中の係数を速度式の次数として用いることができる。
単純反応でなく、中間体を経て進む多段階反応(複合反応)の場合、次数は実験結果によって求める必要がある。
(2)
(1)より正反応の反応式は次の通りである。
\[ V_{1}=K_{1}×[\mathrm{H_{2}}][\mathrm{I_{2}}] \]
H2の濃度が2倍に、I2の濃度が3倍になったということは、[H2]×[I2]は2×3で6倍になったと考えられる。したがって、正反応の速度は6倍になる。
(3)
圧力が4倍になると、体積は4分の1になる。体積が4分の1になると(その分狭くなったスペースにたくさんの分子が閉じ込められるため)濃度は4倍になる。したがって、[H2]と[I2]の濃度がそれぞれ4倍になるので、反応速度は4×4で16倍となる。
\[ V=K×\underbrace{ [\mathrm{H_{2}}] }
_{ \text{ 4倍! }}\underbrace{ [\mathrm{I{2}}] }
_{ \text{ 4倍! }}
\]
A→2B+Cの反応が起こるとする。
一定温度でAの濃度を測定すると下図のようになった。
| t(s) | [A](mol/L) |
|---|---|
| 0 | 9.00 |
| 800 | 3.00 |
(1)0から800秒の平均の速度(mol/(L・s))を求めよ。
(2)反応速度定数(K)の値を求めよ。ただし、単位も明記すること。
(3)実験開始から1200秒後のAの濃度は2.00(mol/L)であった。この時点における瞬間の速さ(mol/(L・s))を求めよ。
解答/解説:タップで表示
解答:(1)7.50×10-3(mol/(L・s))(2)1.25×10-3(/s)(3)2.50×10-3(mol/(L・s))
●STEP1
定義式を用いて、平均の速さを求める。
\[ \begin{align}
\color{red}{\overline{ V }}&=\left|\frac{ [A]_{2}-[A]_{1} }{ t_{2}-t_{1} }\right|
\end{align} \]
●STEP2
速度式を用いて、反応速度定数(K)を求める。
\[ \overline{ V }=\color{red}{K}・[\overline{ A }] \]
●STEP3
速度式を用いて、瞬間の速さを求める。
\[ \begin{align}
\color{red}{V}&=K・[A]
\end{align} \]
まずは、定義式を用いて、平均の速さを求める。
\[ \begin{align}
\overline{ V }&=\left|\frac{ [A]_{2}-[A]_{1} }{ t_{2}-t_{1} }\right|\\
\\
&=\left|\frac{ 3.00-9.00 }{ 800-0 }\right|\\
\\
&=7.50×10^{-3}(\mathrm{mol/(L・s)})
\end{align} \]
次に、速度式(平均の速さ)を用いて反応速度定数(K)を求める。
\[ \begin{align}&\overline{ V }=K・[\overline{ A }]\\
&\leftrightarrow7.50×10^{-3}=K・\frac{ 9.00+3.00 }{ 2 }\\
&\leftrightarrow K=1.25×10^{-3}(\mathrm{/s})\end{align} \]
最後に、速度式(瞬間の速さ)を用いて瞬間の速さを求める。
\[ \begin{align}
V&=K・[A]\\
&=1.25×10^{-3}×2.00\\
&=2.50×10^{-3}(\mathrm{mol/(L・s)})
\end{align} \]














