MENU
ヘスの法則(定義・反応エンタルピーの計算問題の解き方)
はじめに
このページでは『ヘスの法則(定義・反応エンタルピーの計算問題の解き方)』について解説しています。
ヘスの法則(総熱量保存の法則)
- 反応エンタルピー(ΔH)は一般に測定により求められるが、反応によっては測定が困難な場合がある。
- そのような場合、ヘスの法則を利用して反応エンタルピーを計算で導き出す。
ヘスの法則とは
●ヘスの法則(総熱量保存の法則)
「化学変化に伴う反応エンタルピーは、反応前後の状態で決まり、反応経路によって変化しない」
- 「化学変化に伴う反応エンタルピーは、反応前後の状態で決まり、反応経路によって変化しない」これがヘスの法則(総熱量保存の法則)である。
- つまり、反応エンタルピーは”最初と最後の状態だけで決まる”ということである。
- 例えば、「A→B ΔH=QkJ」という熱化学反応式の反応エンタルピーQを求めたいが、測定が困難である場合を考える。
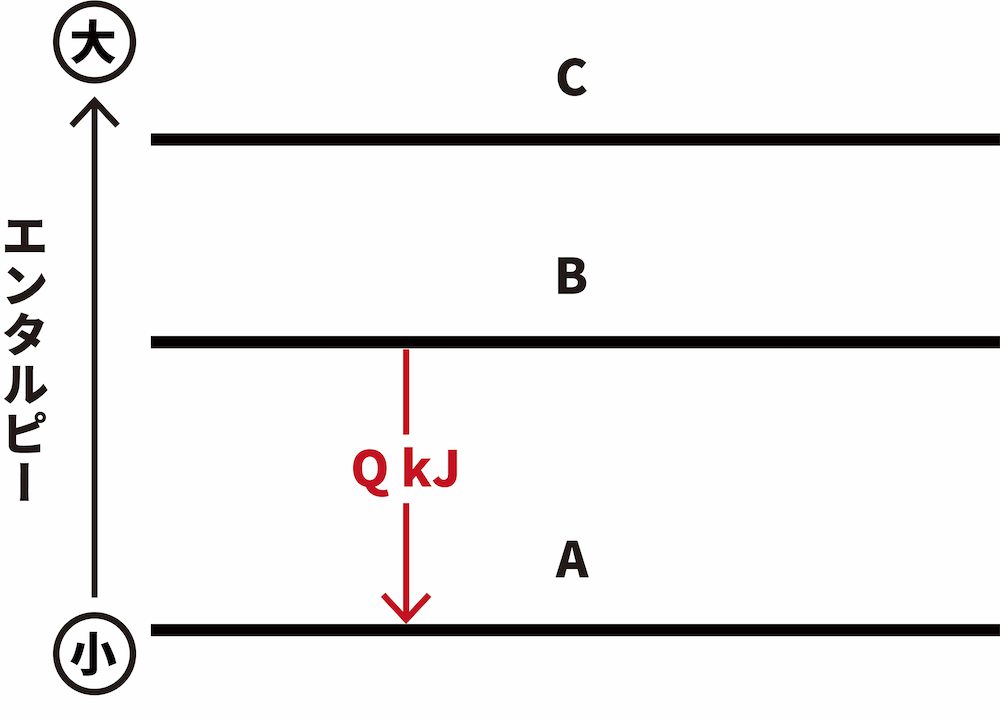
- このとき、CからA、CからBに変化するときに出入りする反応エンタルピー Q1、Q2を用いて次のように表すことができる。
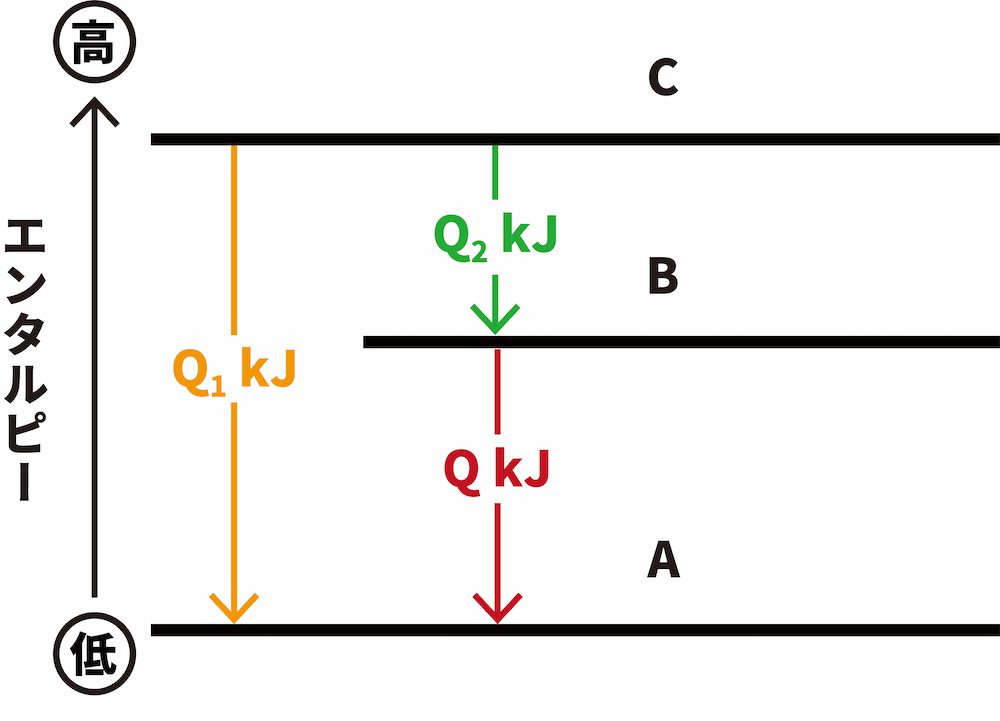
- ヘスの法則より、Q1とQを足したものがQ2となるため、この関係を利用してQを求めるわけである。
ヘスの法則の利用
- ヘスの法則を利用できる実例を紹介する。
- 「❶炭素C(黒鉛)と酸素O2から一酸化炭素COを生じる反応の反応エンタルピー(COの生成エンタルピー)」は、二酸化炭素CO2を生じる副反応が同時に起こるため、直接測定することが難しい。
\[ \mathrm{C(黒鉛)+\frac{ 1 }{ 2 }O_{2}(気)\longrightarrow CO(気)~~~ΔH=QkJ・・・\color{red}{❶}} \]
- そこで、測定することが可能な「❷C(黒鉛)の燃焼エンタルピー」と「❸COの燃焼エンタルピー」を用いることにより、間接的にCOの生成エンタルピーを求めることができる。
\[ \begin{align}
&\mathrm{C(黒鉛)+O_{2}(気)\longrightarrow CO_{2}(気)}~~~ΔH= -394\mathrm{kJ} ・・・\color{orange}{❷}\\
&\mathrm{CO(気)+\frac{ 1 }{ 2 }O_{2}(気)\longrightarrow CO_{2}(気)}~~~ΔH= -283\mathrm{kJ}・・・\color{green}{❸}
\end{align}\]
- ❶❷❸のエンタルピーをエンタルピー図で表現すると次のようになる。
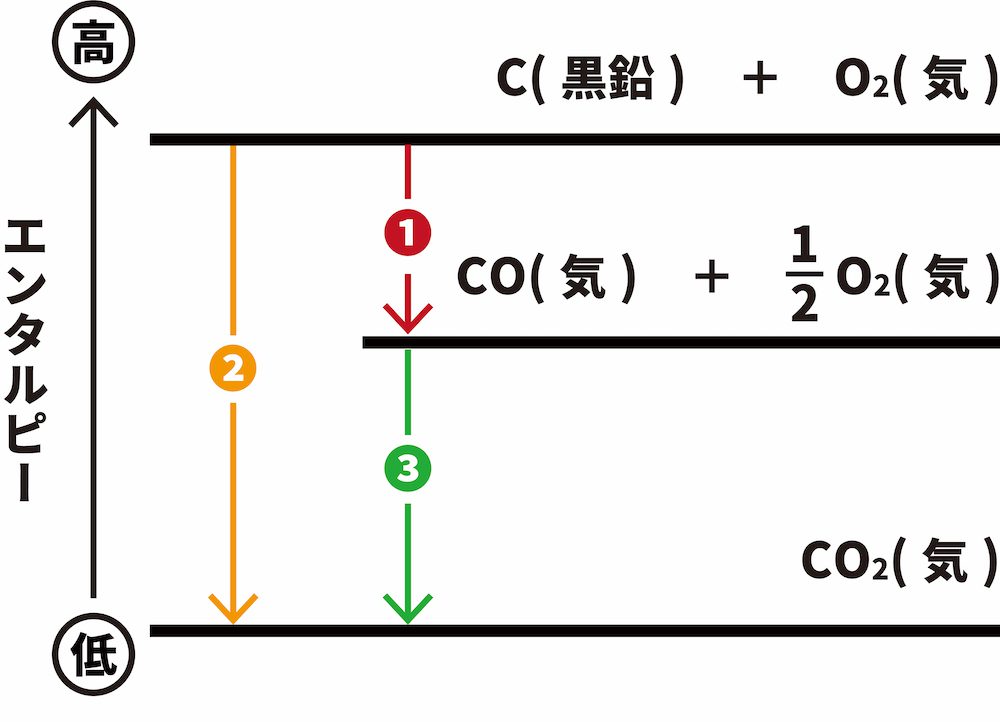
- ヘスの法則より、❶=❷ー❸のため、❶は次のように求めることができる。
\[ \begin{align}
\color{red}{❶}&=\color{orange}{❷}-\color{green}{❸}\\
&=-394-(-283)\\
&=-111~\mathrm{kJ}
\end{align}\]
- よって、COの生成エンタルピーΔHは、ー111kJ/mol である。
反応エンタルピーに関する計算問題
- 反応エンタルピーに関する計算問題の解き方について、例題を用いて解説する。
例題1
次に示す熱化学反応式を用いて、エチレンの燃焼エンタルピーを求めよ。
H2(気)+1/2O2(気)→H2O(液) ΔH=ー286kJ
C(固)+O2(気)→CO2(気) ΔH=ー394kJ
2C(固)+2H2(気)→C2H4(気) ΔH=+52KJ
- この問題の解き方について、次の手順で解説する。
●STEP1
求める反応エンタルピーをQkJとし、それを含む熱化学反応式を書く。
●STEP2
STEP1でつくった熱化学反応式の中にある物質を与式から探す。
●STEP3
それらが同じ側にあれば与式の反応エンタルピーをそのまま、逆側にあればマイナスの符号をつけて、全てを足し合わせる。
今回は「エチレンの燃焼熱」を求める問題のため、エチレンの燃焼反応を表す熱化学反応式を書く。
\[ \mathrm{C_{2}H_{4}(気)+3O_{2}(気)→2CO_{2}(気)+2H_{2}O(液)}~~~ΔH=Q\mathrm{kJ} \]
次に、STEP1でつくった熱化学反応式の中にある物質を与式から探す。
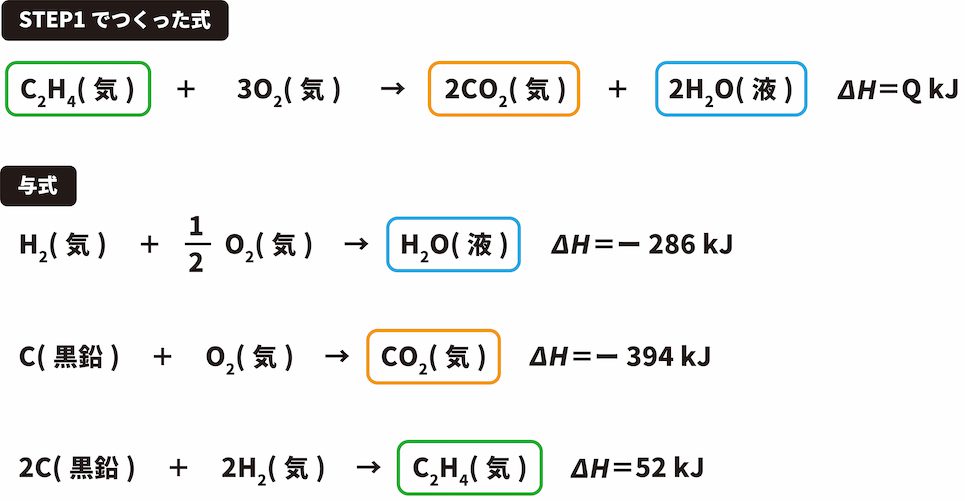
この解法を使うときは、STEP1でつくった式に含まれる物質のうち、2つ以上の与式に出てきている物質(今回の場合、C(黒鉛)、O2(気))は無視する。

CO2は両方の式で右側にあるため、与式の反応エンタルピーである「ー394kJ」をそのまま(ただし、つくった式でのCO2の係数は2のため2をかける)用いる。
C2H4はつくった式では左側にあるに対し、与式では右側にあるため、マイナス(ー)の符号をつけて「ー52kJ」となる。
H2Oは、両方の式で右側にあるため、CO2同様「ー286kJ」をそのまま用いる(ただし、つくった式でのH2Oの係数は2のため2をかける)。
これらの値を全て足し合わせると、求めたい反応エンタルピーを求めることができる。
例題2
メタンCH4の生成反応は次の熱化学反応式で表される。
C(黒鉛)+2H2(気)→CH4(気) ΔH=QkJ
以下の反応エンタルピーを用いてCH4の生成エンタルピーQを求めよ。
黒鉛の燃焼エンタルピー:ー394kJ/mol
メタンの燃焼エンタルピー:ー890kJ/mol
水素の燃焼エンタルピー:ー286kJ/mol
- この問題の解き方について、次の手順で解説する。
●STEP1
問題文で与えられている反応エンタルピーを含む熱化学反応式を書く。
●STEP2
与式の中にある物質をSTEP1でつくった熱化学反応式から探す。
●STEP3
それらが同じ側にあれば与式の反応エンタルピーをそのまま、逆側にあればマイナスの符号をつけて、全てを足し合わせる。
問題文より、反応エンタルピーに関する以下の情報が与えられている。
黒鉛の燃焼エンタルピー:ー394kJ/mol
メタンの燃焼エンタルピー:ー890kJ/mol
水素の燃焼エンタルピー:ー286kJ/mol
これらの反応エンタルピーを含む熱化学反応式を書く。
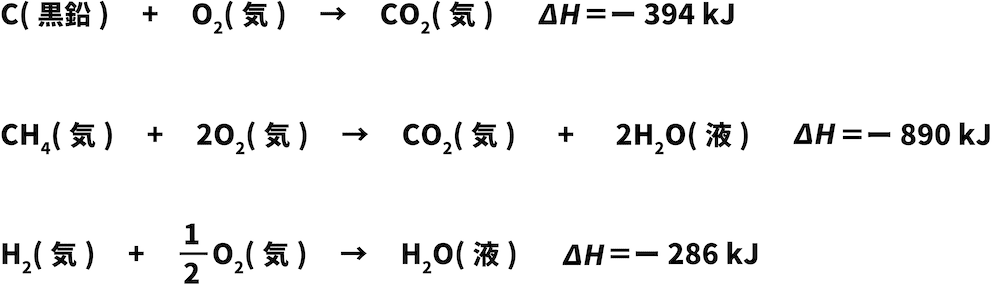
次に、与式の中にある物質をSTEP1でつくった熱化学反応式から探す。
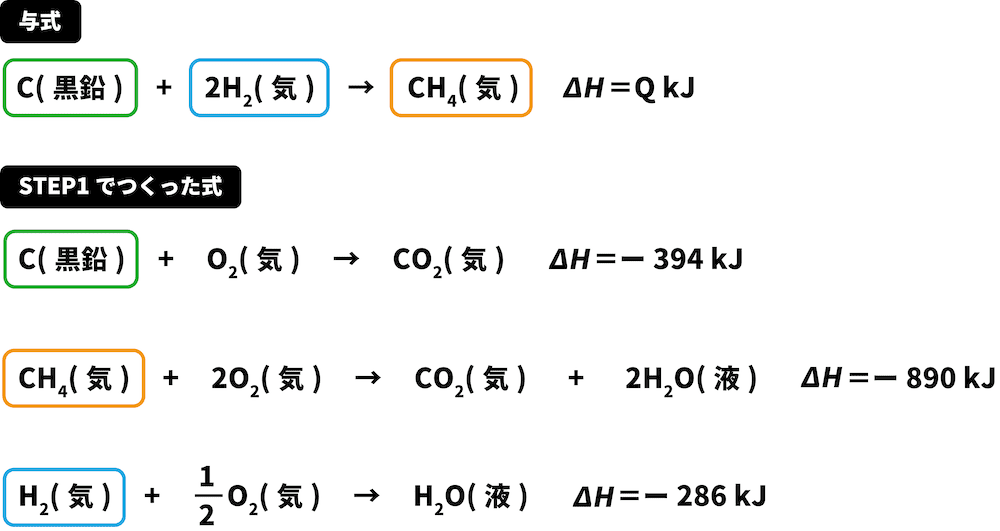
この解法を使うときは、2つ以上の式に出てきている物質(今回の場合、C(黒鉛)、O2(気))は無視する。
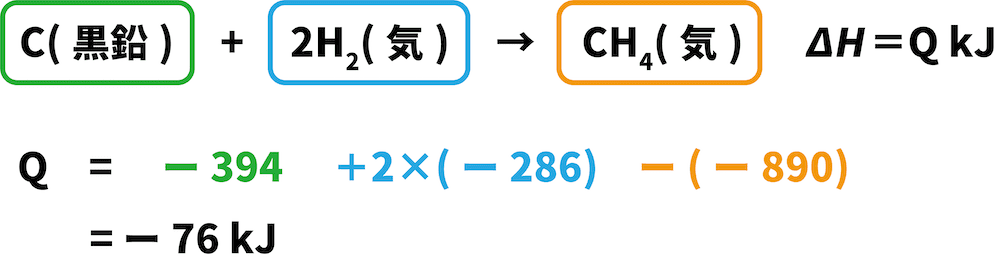
Cは両方の式で左側にあるため、与式の反応エンタルピーである「ー394kJ」をそのまま用いる。
H2は両方の式で左側にあるため、与式の反応エンタルピーである「ー286kJ」をそのまま用いる(ただし、つくった式でのH2の係数は2のため2をかける)。
CH4は与式では右側にあるに対し、つくった式では左側にあるため、マイナス(ー)の符号をつけて「ー(ー890)kJ」となる。
これらの値を全て足し合わせると、求めたい反応エンタルピーを求めることができる。












