MENU
反応熱・エンタルピー・熱化学反応式(図解・比熱の計算など)
はじめに
このページでは『反応熱・エンタルピー・熱化学反応式(図解・比熱の計算など)』について解説しています。
反応熱
- 化学反応に伴い出入りする熱量を反応熱(Q)という。
- 反応熱は通常、着目する物質1molあたりの熱量で表され、単位は〔kJ/mol〕である。
- 熱を発生する化学反応を発熱反応、熱を吸収する化学反応を吸熱反応という。
- 発熱反応ではQ>0、吸熱反応ではQ<0である。
エンタルピー・反応エンタルピー
- 一定圧力下において物質のもつエネルギーをエンタルピー(H)という。
- 一定圧力下での化学反応において、出入りする熱量を反応エンタルピー(ΔH)という。
- ΔHは、「生成物のエンタルピーの和」から「反応物のエンタルピーの和」を引くことで求めることができる。
\[ \mathrm{\mathit{ ΔH }=(生成物のエンタルピーの和)ー(反応物のエンタルピーの和)} \]
発熱反応の反応エンタルピー
- 発熱反応(Q>0)では、反応物から熱(エネルギー)が外に放出されるため、「反応物のエンタルピーの和」よりも「生成物のエンタルピーの和」が小さくなる。つまり、ΔH<0である。
例)メタンCH4の燃焼反応(CH4 + 2O2 → CO2 + 2H2O)
- メタンCH4の燃焼反応では、反応物のエンタルピーの和(CH4 1molと酸素O2 2molのエンタルピーの和)が生成物のエンタルピーの和(CO2 1molとH2O 2molの和)よりも891kJ大きい。したがって、その差分だけ外部にエネルギーとして放出されるため、発熱反応となる。
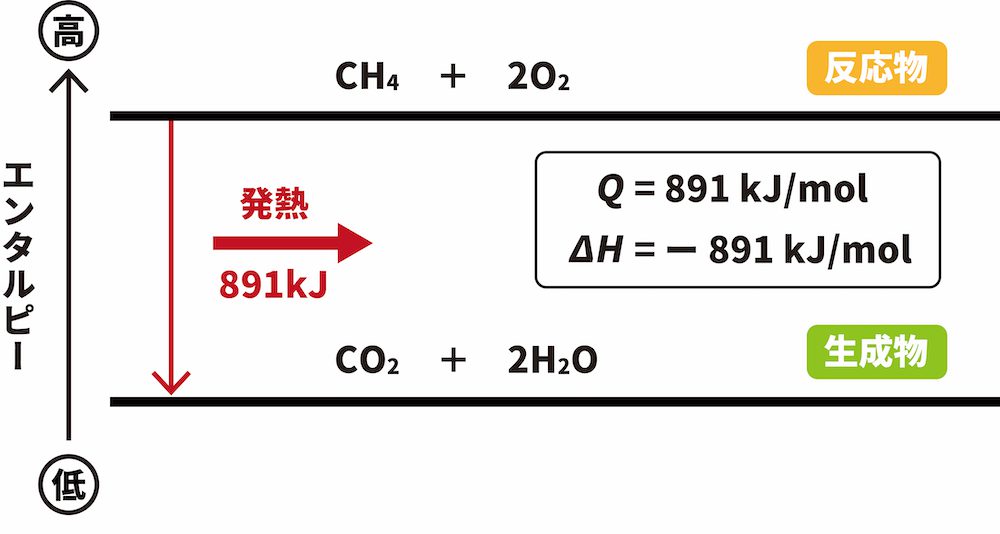
- この反応において、Q=891kJ/mol、ΔH=ー891kJ/molである。
上図のように、各物質のエンタルピーの大きさを表した図をエンタルピー図といいます。エンタルピー図では、エンタルピーの大きな物質を上に、エンタルピーの小さな物質を下に書きます。発熱反応では「反応物のエンタルピーの和」よりも「生成物のエンタルピーの和」が小さくなるため、反応物を上に、生成物を下に書きます。また、それに加えて反応の方向を示す下向きの矢印を記載します。
吸熱反応の反応エンタルピー
- 吸熱反応(Q<0)では、反応物が外から熱(エネルギー)を吸収するため、「反応物のエンタルピーの和」よりも「生成物のエンタルピーの和」が大きくなる。つまり、ΔH>0である。
例)黒鉛Cと水蒸気H2Oの反応(C(黒鉛) + H2O → CO + H2)
- 黒鉛Cと水蒸気H2Oの反応では、反応物のエンタルピーの和(C 1molとH2O 1molのエンタルピーの和)が生成物のエンタルピーの和(CO 1molとH2 1molの和)よりも131kJ小さい。したがって、その差分だけ外部からエネルギーが吸収されるため、吸熱反応となる。
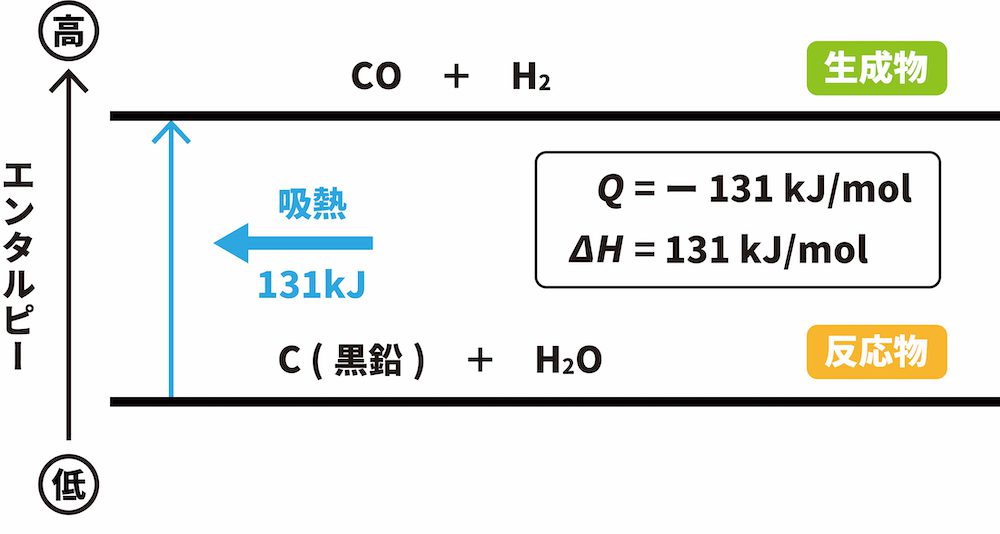
- この反応において、Q=ー131kJ/mol、ΔH=131kJ/molである。
吸熱反応では「反応物のエンタルピーの和」よりも「生成物のエンタルピーの和」が大きくなるため、反応物を下に、生成物を上に書きます。また、それに加えて反応の方向を示す上向きの矢印を記載します。
反応熱と反応エンタルピーの関係
- 発熱反応、吸熱反応における反応熱と反応エンタルピーの関係をまとめる。
| 発熱反応 | 吸熱反応 | |
|---|---|---|
| 反応熱(Q) | >0 | <0 |
| 反応エンタルピー(ΔH) | <0 | >0 |
- 発熱反応(Q>0)では、反応系(反応に関わる物質の集まり)のエンタルピーは減少するため、ΔH<0となる。
- 吸熱反応(Q<0)では、反応系のエンタルピーは増加するため、ΔH>0となる。
反応熱(Q)と反応エンタルピー(ΔH)は大きさが等しく、符号が逆になります。また、両方とも単位はkJ/molです。
反応系と外界
- 反応に関わる物質の集まりを反応系、その外側の世界を外界という。
- 反応熱Qは外界のエネルギー量の増減を表しているのに対し、反応エンタルピーΔHは反応系のもつエネルギー量の増減を表している。
- 発熱反応では反応系から外界にエネルギーが放出されるため外界ではQ>0となる。一方、反応系のもつエネルギー量は放出された分だけ減少するため、ΔH<0となる。
- 吸熱反応では反応系に外界からエネルギーが吸収されるため外界ではQ<0となる。一方、反応系のもつエネルギー量は吸収された分だけ増加するため、、ΔH>0となる。
熱化学反応式
- 化学反応式に反応エンタルピーを加えた式を熱化学反応式という。
- 熱化学反応式を書く手順は次の通りである。
●STEP1
着目する物質の係数を1とし、化学反応式を書く。
●STEP2
各物質の状態を書く。
●STEP3
反応エンタルピーの値に、発熱反応では「ー」、吸熱反応では「+」をつけ、反応式の後に書く。
- 例として次の問題を解いてみよう。
次の反応を熱化学反応式で表せ。
気体の水素H21molを完全燃焼させたとき、液体の水が生成し、286kJの熱が発生した。
まず、着目する物質の係数を1とし、化学反応式を書く。
今回の場合は、水素H2の完全燃焼のため、H2の係数を1とする。
\[ \mathrm{H_{2} + \frac{ 1 }{ 2 }O_{2} \longrightarrow H_{2}O} \]
このとき、着目する物質以外の物質の係数は、分数になっても構いません。
次に、各物質の状態を書く(物質の状態が明らかな場合は省略も可)。
\[ \mathrm{H_{2}(気) + \frac{ 1 }{ 2 }O_{2}(気) \longrightarrow H_{2}O(液)} \]
最後に、反応エンタルピーの値に、発熱反応では「ー」、吸熱反応では「+」をつけ、反応式の後に書く。
\[ \mathrm{H_{2}(気) + \frac{ 1 }{ 2 }O_{2}(気) \longrightarrow H_{2}O(液)}~~~ΔH = -286\mathrm{kJ} \]
反応エンタルピー(ΔH)の単位はkJ/molですが、熱化学反応式では着目する物質の係数(物質量)を1としているので、単位はkJと書きます。
反応エンタルピーの種類
- 反応エンタルピーには、いくつか種類が存在する。
燃焼エンタルピー
- 1molの物質が完全燃焼するときの発熱量を燃焼エンタルピーという。
ex)炭素C(黒鉛)の燃焼エンタルピー
\[ \mathrm{C(黒鉛)+O_{2}(気)\longrightarrow CO_{2}(気)}~~~ΔH = -394\mathrm{kJ} \]
元素に同素体が存在する場合は、その名称を記載しましょう。例えば炭素の場合、C(黒鉛)、C(ダイヤモンド)のようになります。
参考:同素体・同位体(違い・例・硫黄・炭素・酸素・リンなど)
生成エンタルピー
- 1molの化合物が、成分元素の単体から生成するときの発熱量および吸熱量を生成エンタルピーという。
ex)水H2O(液)の生成エンタルピー
\[ \mathrm{H_{2}(気)+ \frac{ 1 }{ 2 }O_{2} \longrightarrow H_{2}O(液)}~~~ΔH = -286\mathrm{kJ} \]
溶解エンタルピー
- 1molの物質が多量の水に溶解したときの発熱量および吸熱量を溶解エンタルピーという。
ex)水酸化ナトリウムNaOH(固)の溶解エンタルピー
\[ \mathrm{NaOH(固)+aq \longrightarrow NaOHaq}~~~ΔH= -44.5\mathrm{kJ} \]
“aq”とは、ラテン語の”aqua(アクア:水)”の略語です。化学や化学基礎で”aq”と書かれている場合は、”大量の水”を指します。例えば”NaOHaq”は”ごく薄い水酸化ナトリウム水溶液”のことです。
参考:【定義】水に溶ける(溶解する)とは一体どういう現象なのか図を用いて解説!
中和エンタルピー
- 酸と塩基の中和反応が起こり、1molの水が生じるときの発熱量を中和エンタルピーという。
ex)水酸化ナトリウムNaOH水溶液と塩酸HClの中和反応の中和エンタルピー
\[ \mathrm{NaOHaq+HClaq \longrightarrow NaClaq+H_{2}O(液)}~~~ΔH = -56.5\mathrm{kJ} \]
状態変化を熱化学反応式で表現する方法
- 物質の状態変化も熱化学反応式で表すことができる。
蒸発エンタルピー
- 1molの液体が気体になるときの吸熱量を蒸発エンタルピーという。
ex)水H2O(液)の蒸発エンタルピー
\[ \mathrm{H_{2}O(液) \longrightarrow H_{2}O(気)}~~~ΔH = 44\mathrm{kJ} \]
融解エンタルピー
- 1molの固体が液体になるときの吸熱量を融解エンタルピーという。
ex)水H2O(固)の融解エンタルピー
\[ \mathrm{H_{2}O(固) \longrightarrow H_{2}O(液)}~~~ΔH = 6.0\mathrm{kJ} \]
昇華エンタルピー
- 1molの固体が気体になるときの吸熱量を昇華エンタルピーという。
ex)水H2O(固)の昇華エンタルピー
\[ \mathrm{H_{2}O(固) \longrightarrow H_{2}O(気)}~~~ΔH = 51\mathrm{kJ} \]
反応エンタルピーの測定(比熱の計算)
- 反応エンタルピーの測定は、外部との熱の出入りがない断熱容器(熱量計)内で行う。
- 熱量は次の公式により求めることができる。
熱量〔J〕=質量〔g〕× 比熱〔J/(g・K)〕× 温度変化〔K〕
- 熱量の求め方について例題を用いて解説する。
例題1
硝酸カリウムKNO3 2.0 g を水 98 g に溶かすと、温度が 1.7 K 低下した。この反応を熱化学反応式で表せ。ただし、反応エンタルピーは整数値〔kJ〕で表し、水溶液の比熱は 4.1〔J/(g・K)〕、KNO3=101とする。
- 温度が低下しているため、この反応は吸熱反応である。
- 問題文で与えられている値を先述の公式に代入する。
\[ \begin{align}熱量〔\mathrm{J}〕&= 質量〔\mathrm{g}〕× 比熱〔\mathrm{J/(g・K)}〕× 温度変化〔\mathrm{K}〕\\
\leftrightarrow 熱量〔\mathrm{kJ}〕&= 質量〔\mathrm{g}〕× 比熱〔\mathrm{kJ/(g・K)}〕× 温度変化〔\mathrm{K}〕\\
&=(\underbrace{2.0~\mathrm{g}}
_{\mathrm{KNO_{3}}}
+
\underbrace{98~\mathrm{g}}
_{\mathrm{H_{2}O}})
×4.1×10^{-3}~\mathrm{kJ/(g・K)}×1.7~\mathrm{K}\\
&=0.697~\mathrm{kJ}
\end{align} \]
- この値を用いて、KNO3 1 mol あたりの吸熱量は次のように求めることができる。
\[ \begin{align}
&\frac{0.697~\mathrm{kJ}}{\frac{2.0~\mathrm{g}}{101~\mathrm{g/mol}}}\\
&=0.697~\mathrm{kJ}×\frac{101~\mathrm{g/mol}}{2.0~\mathrm{g}}\\
&\fallingdotseq 35~\mathrm{kJ/mol}
\end{align} \]
- 以上より、熱化学反応式は次のようになる。
\[ \mathrm{KNO_{3}(固)+H_{2}O(液)\longrightarrow KNO_{3}aq}~~~ΔH = 35\mathrm{kJ} \]
例題2
以下の反応について、問いに答えよ。ただし、水の比熱は 4.2〔J/(g・K)〕、KNO3=101とする。
C(黒鉛)+O2(気)→CO2(気) ΔH=ー394 kJ
(1)24gの黒鉛が完全燃焼したとき、発熱量は何kJか(整数値で解答)。
(2)(1)で発生した熱量を全て水 20 kg に吸収させたとき、水の温度は何K上昇するか(有効数字2桁で解答)。
(1)
- 問題文より、ΔH=ー394 kJ のため、C(黒鉛)1 mol が完全燃焼した際の発熱量は394kJである。
- C 1 mol の質量は次の通りである。
\[ \mathrm{12~g/mol×1~mol=12~g} \]
- したがって、24gの黒鉛が完全燃焼したときの発熱量〔kJ〕は次のように求めることができる。
\[ \begin{align}&394~\mathrm{kJ}×\frac{24~\mathrm{g}}{12~\mathrm{g}} \\
&=788~\mathrm{kJ}
\end{align}\]
(2)
- 問題文で与えられている値を先述の公式に代入する。
\[ \begin{align}&熱量〔\mathrm{J}〕= 質量〔\mathrm{g}〕× 比熱〔\mathrm{J/(g・K)}〕× 温度変化〔\mathrm{K}〕\\
&\leftrightarrow788×10^{3}~\mathrm{J}= 20×10^{3}~\mathrm{g}×4.2~\mathrm{J/(g・K)}×t~\mathrm{K}\\
&\leftrightarrow t \fallingdotseq 9.4~\mathrm{K}
\end{align} \]














