放射性同位体（例・一覧・各種壊変、入試問題の解き方など）

【プロ講師解説】このページでは『放射性同位体の定義から性質、放射性同位体を使った入試問題の解法』について解説しています。解説は高校化学・化学基礎を扱うウェブメディア『化学のグルメ』を通じて6年間大学受験に携わるプロの化学講師が執筆します。

放射性同位体

同位体の中には原子核が”不安定”で放射線を出しながら崩壊（壊変）していくものがあり、このような同位体を放射性同位体という。

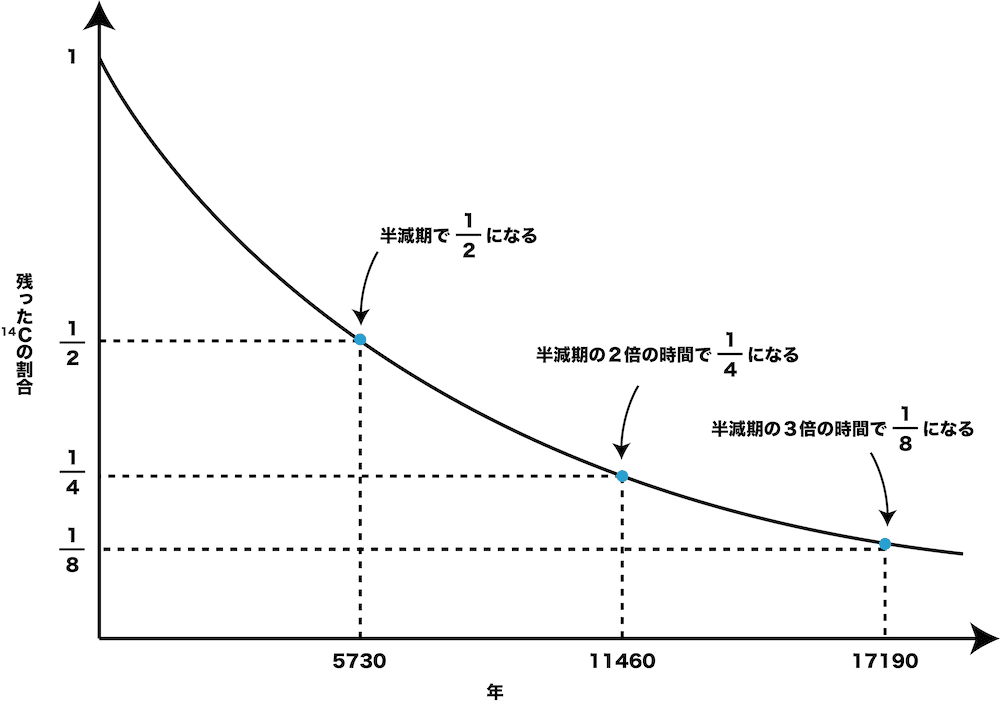
放射性同位体は遺物の年代測定などに利用される。具体例としては、放射性同位体である¹⁴Cを用いた遺跡の年代測定が挙げられる。生きている木は、空気中に存在するの二酸化炭素から¹⁴Cが補給されるので、生体内の¹⁴Cの割合は一定に保たれる。しかし、枯れると¹⁴Cが補給されなくなり、¹⁴Cが放射線を出しながら減少していく。枯れて地中に埋もれた木の¹⁴Cは、約5730年経過するごとに半分になっていく。（半分になるまでの時間を半減期という。）

α（アルファ）壊変

α線（＝ヘリウムの原子核）を放出する。
ヘリウムの原子核は「陽子２個＋中性子２個」で構成されているので、α壊変が一回起こると原子番号は２減少、質量数は４減少する。

β（ベータ）壊変

β線（＝電子）を放出する。
放出される電子は中性子が陽子に変化することで放出されるので、β壊変が一回起こると質量数は変わらないが原子番号は１増加する。

γ（ガンマ）壊変

γ線（＝α、β壊変の後に出る余分なエネルギー）を放出する。質量数や原子番号に変化はない。

放射性同位体が絡んだ問題例

問題

表を見て、以下の問いに答えなさい。

水素	¹H	99.99％
	²H	0.01％
	³H	極微量
炭素	¹²C	98.90％
	¹³C	1.10％
	¹⁴C	極微量
酸素	¹⁶O	99.76％
	¹⁷O	0.04％
	¹⁸O	0.20％

（１）
水素の同位体の１つである³Hは放射性同位体であり、ベータ線（β^–）を放出する。この交換過程で生成する元素の記号を、解答例にならって、質量数をつけて記せ。（解答例：¹³C）

（２）
炭素の同位体の１つである¹⁴Cの原子核中の陽子数と中性子数を記せ。

（３）
天然に存在する炭素は¹²Cと¹³Cの2種類の同位体のみを含むとして、炭素の原子量を有効数字４桁まで求めよ。

（４）
大気の二酸化炭素中には、放射性同位体である¹⁴Cが存在する。生物体は、生きている限り大気中と同じ存在比で¹⁴Cを保持しているが、死滅すると外界からの¹⁴Cの取り込みが停止する。ある地層から出土した木片の極微量の¹⁴Cの存在比を測定したところ、現在の存在比の1/4であることがわかった。この木は何年前まで生存していたかを推定し、有効数字３桁で答えよ。ただし、¹⁴Cの半減期は5700年とし、大気中の¹⁴Cの存在比は数万年前から現在まで一定であると仮定する。

（１）

解答：³He

β線を放出すると書かれているので、この時起こっているのはβ壊変。β壊変では中性子１つが陽子に変化するので、原子番号が１つ増加する。また「陽子数＋中性子数＝質量数」（詳しくは【原子の構造】陽子・中性子・電子・原子核・質量数・原子番号の数と関係を参照）なので、質量数は変化しない。

（２）

解答：陽子数６　中性子数 8

¹⁴Cの質量数は14。Cの原子番号は6なので、陽子の数は６、中性子の数は8となる。（詳しくは【原子の構造】陽子・中性子・電子・原子核・質量数・原子番号の数と関係を参照）

（３）

解答：12.01

同位体の相対質量に、それぞれの存在比をかけて足す。

\[
\mathtt{ \underbrace{12.0 × \frac{ 98.9 }{ 100 } }
_{ ^{ 12 }\text{ C }} +
\underbrace{13.0 × \frac{ 1.1 }{ 100 } }
_{ ^{ 13 }\text{ C }} = 12.011}
\]

約12になった。これが炭素の原子量。
ちなみに、このような原子量計算をするときの有名な工夫がある。

\[
\mathtt{ 12.0 × \frac{ 98.9 }{ 100 } + 13.0 × \frac{ 1.1 }{ 100 } \\
= 12.0 × \frac{ 98.9 }{ 100 } + (12.0+1.00) × \frac{ 1.1 }{ 100 } \\
= 12.0 × \frac{ 98.9 }{ 100 } + 12.0 × \frac{ 1.1 }{ 100 } + 1.00 × \frac{ 1.1 }{ 100 }\\
= 12.0 × (\frac{ 98.9 }{ 100 } + \frac{ 1.1 }{ 100 }) + 1.00 × \frac{ 1.1 }{ 100 }\\
= 12.0 × 1 + 1.00 × \frac{ 1.1 }{ 100 }\\
= 12.0 + 0.011\\
= 12.011}
\]

※同位体の存在比や原子量を使った計算についてさらに詳しくは同位体（一覧・例・性質・存在比を使った計算など）を参照

（４）

解答：1.14×10⁴年

半減期はその同位体の存在比が半分になるまでに掛かる時間である。
したがって、存在比が1/4になっているということは半減期が二回訪れているはずなので、

\[
\mathtt{ 5700×2=11400}
\]

答えは11400年（1.14×10⁴年）となる。

演習問題

問１

【】に当てはまる用語を答えよ。

陽子の数が同じで中性子の数が異なる原子同士を互いに【１】という。【１】の中には、不安定で【２】を出しながら壊れる（別の元素に変化する）ものがあり、それらを総称して【３】という。また、【２】を出す性質（能力）のことを【４】という。【３】が壊れて半分の量になる時間のことを【５】といい、これを利用して遺跡の年代測定などが行われる。

【問１】解答/解説：タップで表示

解答：【１】同位体【２】放射線【３】放射性同位体（ラジオアイソトープ）【４】放射能【５】半減期