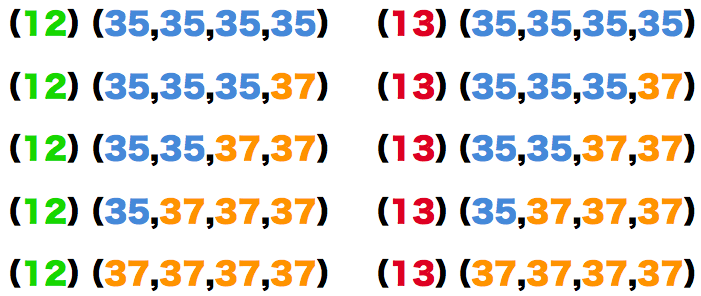MENU
同位体(一覧・例・性質・存在比を使った計算など)
はじめに
【プロ講師解説】このページでは『同位体(一覧・例・性質・存在比を使った計算など)』について解説しています。
同位体とは
- 原子番号が同じで、質量数の異なる原子同士を同位体という。
- 例として水素を紹介する。水素は、天然に3つの同位体が存在する。
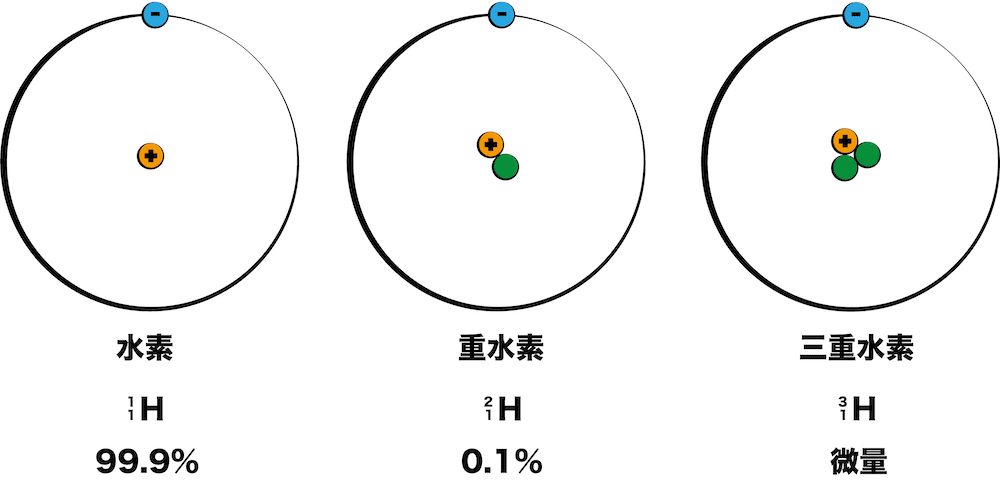
- これら3つは、同じ”水素”の仲間ではあるが、質量数が異なっている。原子番号(=陽子の数)が一緒であるにも関わらず質量数が違うということはつまり「中性子の数が異なっている」ということである。
参考:【原子の構造】陽子・中性子・電子・原子核・質量数・原子番号の数と関係
- 同位体により存在比が異なることにも注意が必要である。普通の水素が1番多く99.9%、次が重水素で0.1%、三重水素はほとんど存在しない。
- 同位体は、陽子や電子の数が等しいため、化学的性質(反応性など)にあまり違いがない。(ちなみに、同素体は化学的性質に違いがある)
同位体の存在比
- 代表的な同位体の存在比を次に示す。
水素
| 同位体 | 存在比 |
|---|---|
| 1H | 99.985% |
| 2H | 0.015% |
炭素
| 同位体 | 存在比 |
|---|---|
| 12C | 98.90% |
| 13C | 1.10% |
窒素
| 同位体 | 存在比 |
|---|---|
| 14N | 99.634% |
| 15N | 0.366% |
酸素
| 同位体 | 存在比 |
|---|---|
| 16O | 99.762% |
| 17O | 0.038% |
| 18O | 0.200% |
塩素
| 同位体 | 存在比 |
|---|---|
| 35Cl | 75.77% |
| 37Cl | 24.23% |
銅
| 同位体 | 存在比 |
|---|---|
| 63Cu | 69.17% |
| 65Cu | 30.83% |
放射性同位体
- 同位体の中には原子核が“不安定”で放射線を出しながら崩壊(壊変)していくものがあり、このような同位体を放射性同位体という。
- 放射性同位体は遺物の年代測定・医療などに利用される。
壊変
- 放射性同位体の壊変には、いくつか種類が存在する。
α(アルファ)壊変
- α線(=ヘリウムの原子核)を放出する。
- ヘリウムの原子核は「陽子2個+中性子2個」で構成されているため、α壊変が1回起こると原子番号は2減少、質量数は4減少する。
β(ベータ)壊変
- β線(=電子)を放出する。
- 放出される電子は中性子が陽子に変化することで放出されるため、β壊変が1回起こると原子番号は1増加、質量数は変化しない。
γ(ガンマ)壊変
- γ線(=α、β壊変の際に出る余分なエネルギー)を放出する。質量数や原子番号に変化はない。
同位体の存在比を使って物質量比を求める問題
- 同位体の存在比を使って物質量比を求める問題の解き方を解説する。
銅粉15.9gを加熱し完全に酸化したところ、黒色の酸化銅(Ⅱ)19.9gが生成した。この酸化銅(Ⅱ)に含まれる63Cuと65Cuの物質量の比を求めよ。ただし、63Cuの相対質量は63.0、65Cuの相対質量は65.0とする。
- この問題は、3STEPで解くことができる。
まずは、反応したO2のmolを求める。この反応の反応式は次の通りである。
\[ \mathrm{2Cu + O_2 → 2CuO}\]
銅Cuに酸素O2がくっついて酸化銅(Ⅱ)CuOが生成しているため、生成したCuOの質量から銅の質量を引くことで、CuにくっついたO2の質量を求めることができる。
\[ \mathrm{19.9(g) – 15.9(g) = 4.0(g)}\]
O2のモル質量(分子量)は32(g/mol)なので、O2のmolは次のように求めることができる。
\[ \mathrm{4.0(g) ÷ 32(g/mol) = 0.125(mol)}\]
次に、STEP1で求めたO2のmolからCuのmolを求め、それを使ってCuの見かけ上のモル質量(原子量)を求めていく。もう一度反応式を確認する。
\[ \mathrm{2Cu + O_2 → 2CuO}\]
CuとO2の係数比は2:1である。したがって、この反応に必要なCuのmolは、O2の2倍のはずなので…
\[ \mathrm{0.125(mol) × 2 = 0.25(mol)}\]
この値を使って、Cuの見かけ上のモル質量(原子量)を求めていく。反応で使われたCuは問題文に書いてある通り15.9gなので…
\[ \mathrm{15.9(g) ÷ 0.25(mol) = 63.6(g/mol)}\]
最後に、同位体の片方の存在比をxとおき、式を立ててxを求めていく。
\[ \mathrm{63.0 × x + 65.0 × (1-x) = 63.6}\]
63Cuの存在比(物質量比)を「x」とすると、65Cuの存在比は「1ーx」と表すことができる。
同位体それぞれの相対質量に存在比をかけたものを足すと、見かけ上の原子量になる。
この式を解いて…
\[ \mathrm{x = 0.7(70%)}\]
したがって、この問題の酸化銅(Ⅱ)Cu2Oに含まれる63Cuと65Cuの物質量比は…
\[ \mathrm{^{63}Cu:^{65}Cu=7:3}\]
同位体の存在比を使って原子量を求める問題
- 同位体の存在比を使って原子量を求める問題の解き方を解説する。
炭素原子の2つの同位体12C(相対質量=12.0),13C(相対質量=13.0)の存在比が、 それぞれ98.9%、1.1%であるとき、炭素の原子量を求めよ。
- 同位体の相対質量に、それぞれの存在比をかけて足す。
\[\underbrace{12.0 × \frac{ 98.9 }{ 100 } }
_{ ^{ 12 }\text{ C }} +
\underbrace{13.0 × \frac{ 1.1 }{ 100 } }
_{ ^{ 13 }\text{ C }} = 12.011 \]
- 約12になった。これが炭素の原子量である。ちなみに、このような原子量計算をするときの有名な工夫がある。
\[ \begin{align}
&12.0 × \frac{ 98.9 }{ 100 } + 13.0 × \frac{ 1.1 }{ 100 } \\
&= 12.0 × \frac{ 98.9 }{ 100 } + (12.0+1.00) × \frac{ 1.1 }{ 100 } \\
&= 12.0 × \frac{ 98.9 }{ 100 } + 12.0 × \frac{ 1.1 }{ 100 } + 1.00 × \frac{ 1.1 }{ 100 }\\
&= 12.0 × (\frac{ 98.9 }{ 100 } + \frac{ 1.1 }{ 100 }) + 1.00 × \frac{ 1.1 }{ 100 }\\
&= 12.0 × 1 + 1.00 × \frac{ 1.1 }{ 100 }\\
&= 12.0 + 0.011\\
&= 12.011
\end{align} \]
同位体の原子量を使って存在比率を求める問題
- 同位体の原子量を使って存在比率を求める問題の解き方を解説する。
塩素原子の原子量が35.5のとき、塩素原子の2つの同位体35Cl(相対質量=35.0),37Cl(相対質量=37.0)の存在比をそれぞれ求めよ。
- こちらも同じように、「同位体の相対質量にそれぞれの存在比をかけて足すと、原子量を求めることができる」ということを利用して解く。
\[\underbrace{35.0 × \frac{ x }{ 100 } }
_{ ^{ 35 }\text{ Cl }} +
\underbrace{37.0 × \frac{ 100-x }{ 100 } }
_{ ^{ 37 }\text{ Cl }} = 35.5 \]
- 片方の存在比(%)をxとおけば、全部で100(%)だからもう片方は100ーx(%)と考えられる。この式をxについて解くと、x=0.75となるため、
\[\begin{align}&
^{35}\mathrm{Cl} = 75(\mathrm{\%}) \\
&^{37}\mathrm{Cl}= 25(\mathrm{\%})
\end{align} \]
同位体まとめ
この『同位体(一覧・例・性質・存在比を使った計算など)』のページで解説した内容をまとめる。
- 原子番号が同じで、質量数の異なる原子同士を同位体という。
- 同位体は、陽子や電子の数が等しいため、化学的性質(反応性など)にあまり違いがない。(⇔同素体は化学的性質に違いがある)
- 同位体の中には原子核が“不安定”で放射線を出しながら崩壊(壊変)していくものがあり、このような同位体を放射性同位体という。
演習問題
原子番号が同じで、質量数の異なる原子同士を【1】という。
解答/解説:タップで表示
解答:【1】同位体
原子番号が同じで、質量数の異なる原子同士を同位体という。
同素体と同位体のうち、化学的性質に違いがみられるのは【1】である。
解答/解説:タップで表示
解答:【1】同素体
同位体は、陽子や電子の数が等しいため、化学的性質(反応性など)にあまり違いがない(⇔同素体は化学的性質に違いがある)。
同位体の中には原子核が“不安定”で放射線を出しながら崩壊(壊変)していくものがあり、このような同位体を【1】という。
解答/解説:タップで表示
解答:【1】放射性同位体
同位体の中には原子核が“不安定”で放射線を出しながら崩壊(壊変)していくものがあり、このような同位体を放射性同位体という。
水素の同位体には、質量数が1の水素、質量数が2の【1】、質量数が3の【2】がある。
解答/解説:タップで表示
解答:【1】重水素(ジュウテリウム)【2】三重水素(トリチウム)
水素の同位体には、質量数が1の水素、質量数が2の重水素(ジュウテリウム)、質量数が3の三重水素(トリチウム)がある。
2種類の炭素原子(12C・13C)と2種類の塩素原子(35Cl・37Cl)を組み合わせて四塩化炭素CCl4をつくるとき、【1】パターンの四塩化炭素が生成し得る。