【プロ講師解説】このページでは『電離平衡（公式の導出・典型的な計算問題の解法など）』について解説しています。解説は高校化学・化学基礎を扱うウェブメディア『化学のグルメ』を通じて6年間大学受験に携わるプロの化学講師が執筆します。
電離平衡・電離定数とは
酢酸の電離平衡
弱電解質（弱酸や弱塩基）を水に溶かすと、完全には電離せず次のような平衡状態に達する。
CH_{3}COOH+H_{2}O⇄CH_{3}COO^{-}+H_{3}O^{+}
\]
このような平衡を（酢酸の）電離平衡という。
ここで、上の式を平衡定数の式で表すと、
K=\frac{ ［CH_{3}COO^{-}］［H_{3}O^{+}］ }{ ［CH_{3}COOH］［H_{2}O］ }=一定
\]
この式中で、H2Oは他の化学種に比べて多量に存在しているため、電離や平衡によって消費・生成する量は（相対的に）ムシすることができる。そこで、［H2O］を一定とみなし…
K［H_{2}O］=\frac{ ［CH_{3}COO^{-}］［H_{3}O^{+}］ }{ ［CH_{3}COOH］ }=一定
\]
このようにできる。
K［H2O］を改めてKaとおき、また［H3O+］は［H+］の形で表しても良いことを考慮すると…
K_{a}=\frac{ ［CH_{3}COO^{-}］［H^{+}］ }{ ［CH_{3}COOH］ }
\]
このような式が導き出される。
このKaを（酢酸の電離平衡における）電離定数という。
アンモニアの電離平衡
アンモニアも弱電解質であり、水に溶かすと電離平衡の状態になる。
NH_{3}+H_{2}O⇄NH_{4}^{+}+OH^{-}
\]
これを平衡定数の式で表すと…
K=\frac{ ［NH_{4}^{+}］［OH^{-}］ }{ ［NH_{3}］［H_{2}O］ }=一定
\]
この式中でH2Oは他の化学種に比べて多量に存在しているため電離や平衡によって生成する量は（相対的に）ムシすることができる。そこで、［H2O］を一定とみなし…
K［H_{2}O］=\frac{ ［NH_{4}^{+}］［OH^{-}］ }{ ［NH_{3}］ }=一定
\]
K［H2O］を改めてKbとおくと…
K_{b}=\frac{ ［NH_{4}^{+}］［OH^{-}］ }{ ［NH_{3}］ }
\]
このような式が得られる。
このKbを（アンモニアの電離平衡における）電離定数という。
電離平衡の公式（導出・まとめ）
酢酸の電離平衡
酢酸のモル濃度をc(mol/L)、電離度をαとすると、電離平衡時の各物質の変化量は次のように表すことができる。
電離定数の式にこれらを代入すると…
\begin{align}
K_{a}&=\frac{ ［CH_{3}COO^{-}］［H^{+}］ }{ ［CH_{3}COOH］ }\\
&=\frac{ cα×cα }{ c(1-α) }\\
&=\frac{ cα^{2} }{ 1-α }
\end{align}
\]
ここで、酢酸の電離度はα<<1（１よりめっちゃ小さい）なので「1-α≒1」と近似できる。 したがって...
\mathbf{【公式１】}\\
K_{a}=cα^{2}\\
\ \\
\mathbf{【公式２】}\\
α=\sqrt{ \frac{ K_{a} }{ c } }\\
\ \\
\mathbf{【公式３】}\\
\begin{align}
［H^{+}］&=cα\\
&=c×\sqrt{ \frac{ K_{a} }{ c } }\\
&=\sqrt{ cK_{a} }
\end{align}
\]
アンモニアの電離平衡
アンモニアのモル濃度をc(mol/L)、電離度をαとすると、電離平衡時の各物質の変化量は次のように表すことができる。
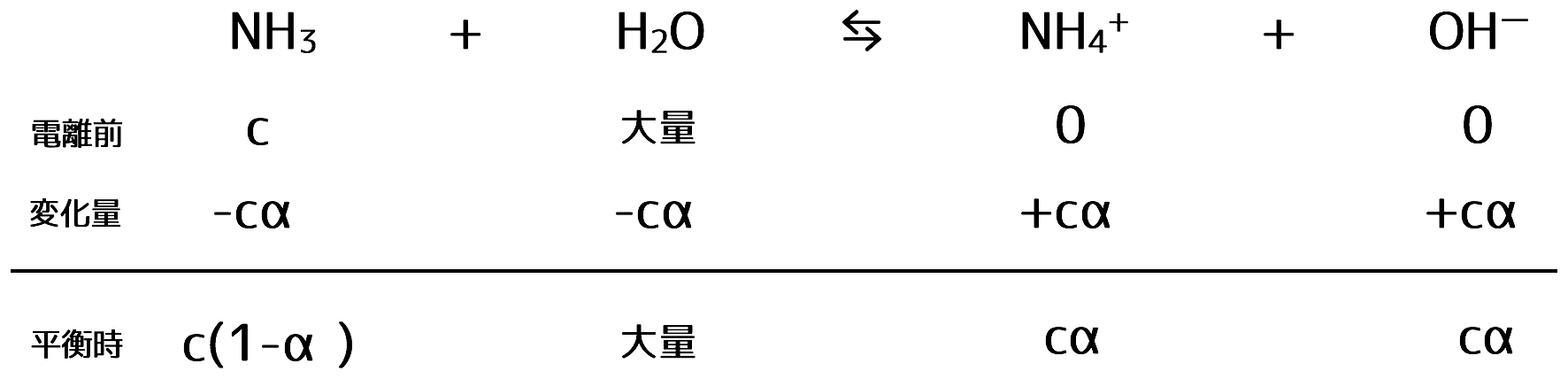
電離平衡の式にこれらを代入すると…
\begin{align}
K_{b}&=\frac{ ［NH_{4}^{+}］［OH^{-}］ }{ ［NH_{3}］ }\\
&=\frac{ cα×cα }{ c(1-α) }\\
&=\frac{ cα^{2} }{ 1-α }
\end{align}
\]
酢酸同様、アンモニアの電離度はα<<1なので「1-α≒1」と近似できる。 したがって...
\mathbf{【公式１】}\\
K_{b}=cα^{2}\\
\ \\
\mathbf{【公式２】}\\
α=\sqrt{ \frac{ K_{b} }{ c } }\\
\ \\
\mathbf{【公式３】}\\
\begin{align}
［OH^{-}］&=cα\\
&=c×\sqrt{ \frac{ K_{b} }{ c } }\\
&=\sqrt{ cK_{b} }
\end{align}
\]
電離平衡の計算問題
電離平衡に関する計算問題を解いてみよう。
（１）0.20mol/Lの酢酸水溶液の電離定数Ka、水素イオン濃度[H+]、pHを求めよ。
（２）0.10mol/Lのアンモニア水溶液の電離定数Kb、水酸化物イオン濃度[OH–]、pHを求めよ。
（１）
まずは電離定数Kaから求めていく。
問題文に酢酸の電離度は0.010と書いてあるので、上でやった【公式１】を用いると…
\begin{align}
K_{a}&=cα^{2}\\
&=0.20×(0.010)^{2}\\
&=2.0×10^{-5}
\end{align}
\]
次に水素イオン濃度[H+]を求める。
公式３を使うと…
\begin{align}
［H^{+}］&=\sqrt{ cK_{a} }\\
&=\sqrt{ 0.20×2.0×10^{-5} }\\
&=2.0×10^{-3}
\end{align}
\]
（ちなみにこの場合は[H+]=cαを使っても求めることができる）
最後にpHを求める。高校化学pH計算完全マスター講座！！で紹介した公式を用いると…
\begin{align}
pH&=-log_{10}［H^{+}］\\
&=-log_{10}(2.0×10^{-3})\\
&=2.7
\end{align}
\]
（２）
まずは電離定数Kbから求めていく。
問題文にアンモニアの電離度は0.010と書いてあるので、上でやった【公式１】を用いると…
\begin{align}
K_{b}&=cα^{2}\\
&=0.10×(0.010)^{2}\\
&=1.0×10^{-5}
\end{align}
\]
次に水酸化物イオン濃度[OH–]を求める。
公式３を使うと…
\begin{align}
［OH^{-}］&=\sqrt{ cK_{b} }\\
&=\sqrt{ 0.10×1.0×10^{-5} }\\
&=1.0×10^{-3}
\end{align}
\]
最後にpHを求める。pHを求めるためにまずは問題文にある[H+][OH–]=1.0×10-14の関係を用いて[H+]を導く。
［H^{+}］［OH^{-}］=1.0×10^{-14}\\
\begin{align}
↔︎［H^{+}］&=\frac{ 1.0×10^{-14} }{ ［OH^{-}］ }\\
&=\frac{ 1.0×10^{-14} }{ 1.0×10^{-3} }\\
&=1.0×10^{-11}
\end{align}
\]
そして…
\begin{align}
pH&=-log_{10}［H^{+}］\\
&=-log_{10}(1.0×10^{-11})\\
&=11
\end{align}
\]
電離平衡に関する演習問題
電離による平衡状態を【１】といい、そのときの平衡定数を【２】という。
関連：計算ドリル、作りました。
化学のグルメオリジナル計算問題集「理論化学ドリルシリーズ」を作成しました！モル計算や濃度計算、反応速度計算など入試頻出の計算問題を一通りマスターできるシリーズとなっています。詳細は【公式】理論化学ドリルシリーズにて！
・化学のグルメ運営代表
・高校化学講師
・薬剤師
・デザイナー/イラストレーター
数百名の個別指導経験あり（過去生徒合格実績：東京大・京都大・東工大・東北大・筑波大・千葉大・早稲田大・慶應義塾大・東京理科大・上智大・明治大など）
2014年よりwebメディア『化学のグルメ』を運営
公式オンラインストアで販売中の理論化学ドリルシリーズ・有機化学ドリル等を執筆
著者紹介詳細