MENU
限界イオン半径比（定義・求め方・配位数との関係など）
目次
はじめに
【プロ講師解説】このページでは『限界イオン半径比（定義・求め方・配位数との関係など）』について解説しています。
イオン結晶の安定性
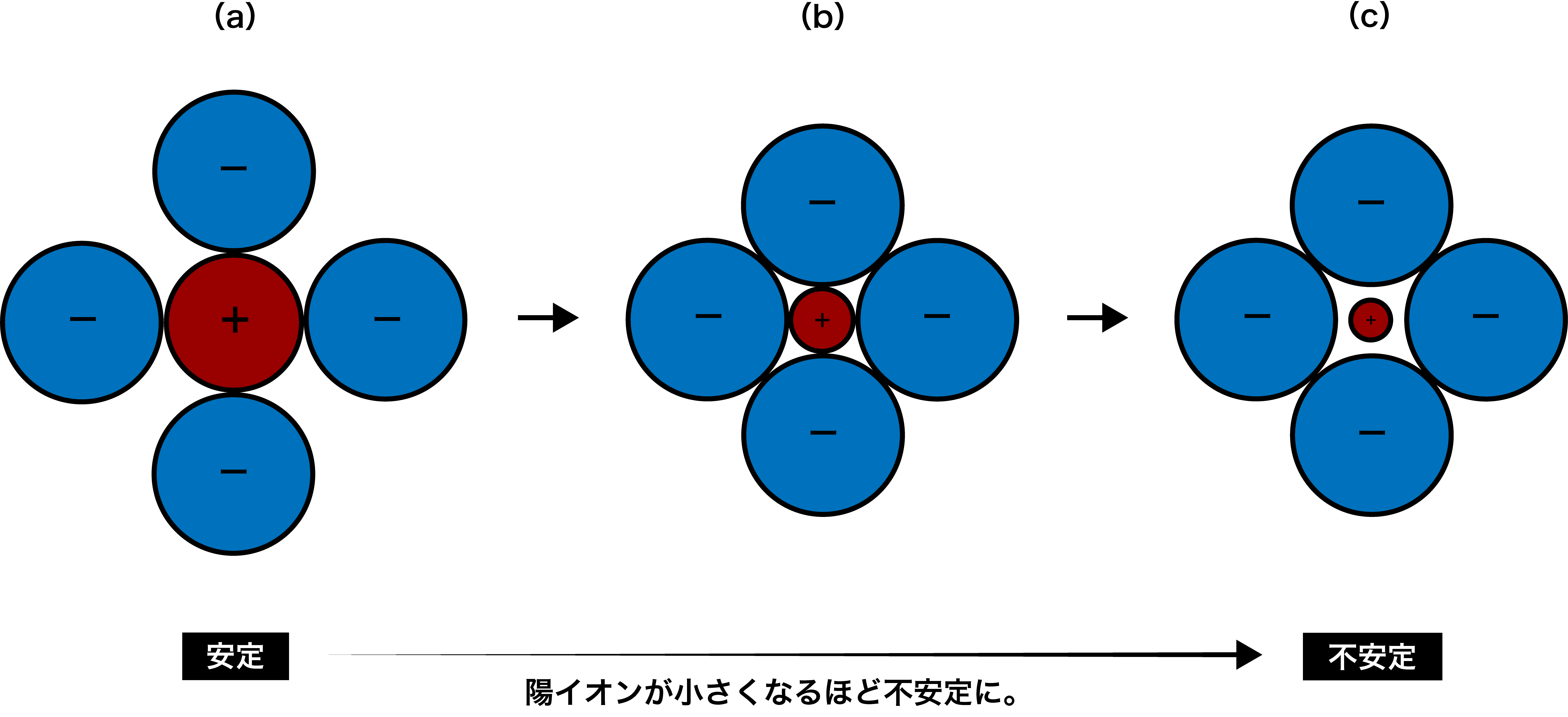
- 下図(a)のように、陽イオンの半径が一定以上の大きさのときは、陰イオン同士は接触しておらず、結晶は安定して存在している。
- 下図(b)のように、陰イオン同士が接触した状態では、結晶はギリギリ安定している。
- 下図(c)のように、陽イオンと陰イオンが接触していない状態では、陰イオン同士が非常に強く反発してしまうため、結晶は不安定になる（存在することができない）。
限界イオン半径比とは
- イオン結晶が、上図(b)のような“安定ギリギリ”の状態にあるときの陽イオン半径r＋と陰イオン半径rーとの比を限界イオン半径比という。
\[
\frac{ r^{＋} }{ r^{ー} }
\]
限界イオン半径比と配位数
- 各イオン結晶の配位数と限界イオン半径比を一覧で示すと次のようになる。
| イオン結晶 | 配位数 | 限界イオン半径比 |
|---|---|---|
| 塩化ナトリウム（NaCl）型構造 | ６ | 0.41〜0.73 |
| 塩化セシウム（CsCl）型構造 | ８ | ≧0.73 |
| 硫化亜鉛（ZnS）型構造 | ４ | ≦0.41 |
- イオン結晶の限界イオン半径比の範囲外になると、そのイオン結晶は不安定となり、配位数の異なる違う結晶構造に変化する。このように、温度や圧力の変化により、結晶構造が変化する現象を相転移という。
参考：【塩化ナトリウム型構造】イオン結晶の配位数・半径・限界半径比まとめ
参考：【塩化セシウム型構造】イオン結晶の配位数・半径・限界半径比まとめ
参考：【硫化亜鉛型構造】イオン結晶の配位数・半径・限界半径比まとめ
限界イオン半径比の求め方
- イオン結晶の代表である『塩化ナトリウム型構造（NaCl型構造）』と『塩化セシウム型構造（CsCl型構造）』の限界イオン半径比の求め方を確認する。
塩化ナトリウム型構造の限界イオン半径の求め方
- 塩化ナトリウム型構造（NaCl型構造）の単位格子を横からみると次のようになる。
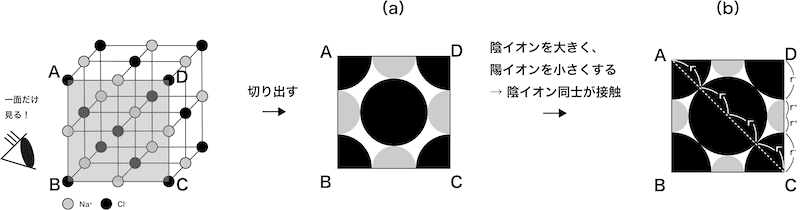
- 上図(b)の「安定ギリギリ」の状態で陽イオン・陰イオンの半径をそれぞれr＋・rーとおく。
- △ABCに着目すると、AC=√2×ABのため…
\[
\begin{align}
2(r^{+}+r^{-})&=\sqrt{ 2 }×2r^{-}\\
↔︎ \frac{ r^{+}+r^{-} }{ r^{-} } &=\sqrt{ 2 } \\
↔︎ \frac{ r^{+}}{ r^{-} } &=\sqrt{ 2 }-1 \geqq 0.41 \\
\end{align}
\]
- 塩化ナトリウム型構造（NaCl型構造）の限界イオン半径比は≧0.41となる。
塩化セシウム型構造の限界イオン半径の求め方
- 塩化セシウム型構造（CsCl型構造）の単位格子を対角線で切り取ると次のようになる。
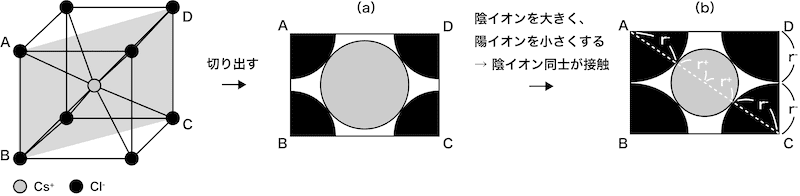
- 上図(b)の「安定ギリギリ」の状態で陽イオン・陰イオンの半径をそれぞれr+・r–とおく。
- △ABCに着目すると、AC=√3×ABのため…
\[
\begin{align}
\mathrm{2(r^{+}+r^{-})}&\mathrm{=\sqrt{ 3 }×2r^{-}}\\
↔︎ \mathrm{\frac{ r^{+}+r^{-} }{ r^{-} }} &\mathrm{=\sqrt{ 3 }} \\
↔︎ \mathrm{\frac{ r^{+}}{ r^{-} }} &\mathrm{=\sqrt{ 3 }-1 \geqq 0.73} \\
\end{align}
\]
限界イオン半径比まとめ
この『限界イオン半径比（定義・求め方・配位数との関係など）』のページで解説した内容をまとめる。
| イオン結晶 | 配位数 | 限界イオン半径比 |
|---|---|---|
| 塩化ナトリウム（NaCl）型構造 | ６ | 0.41〜0.73 |
| 塩化セシウム（CsCl）型構造 | ８ | ≧0.73 |
| 硫化亜鉛（ZnS）型構造 | ４ | ≦0.41 |
演習問題
化学のグルメでは、高校化学・化学基礎の一問一答問題を公開しています。問題一覧は【スマホで出来る】一問一答（高校化学・化学基礎）でご覧下さい。
問1
塩化ナトリウム型構造（NaCl型構造）の限界イオン半径比は0.41〜【１】である。
解答/解説：タップで表示
解答：【１】0.73
塩化ナトリウム型構造（NaCl型構造）の限界イオン半径比は0.41〜0.73である。
問2
塩化セシウム型構造（CsCl型構造）の限界イオン半径比は≧【１】である。
解答/解説：タップで表示
解答：【１】0.73
塩化セシウム型構造（CsCl型構造）の限界イオン半径比は≧0.73である。
問3
硫化亜鉛型構造（ZnS型構造）の限界イオン半径比は≦【１】である。
解答/解説：タップで表示
解答：【１】0.41
硫化亜鉛型構造（ZnS型構造）の限界イオン半径比は≦0.41である。
【高校化学の計算ドリル】大好評発売中！
高校化学・化学基礎の計算問題が苦手な人に向けた計算ドリルを発売しました。豊富な問題数で、入試頻出の計算問題の解き方を身につけることができます。
