MENU
異性体(種類・数え方・分類など)
目次
はじめに
【プロ講師解説】このページでは『異性体(種類・数え方・分類など)』について解説しています。
異性体とは
- 分子式が同じで、構造が異なる物質同士を異性体という。
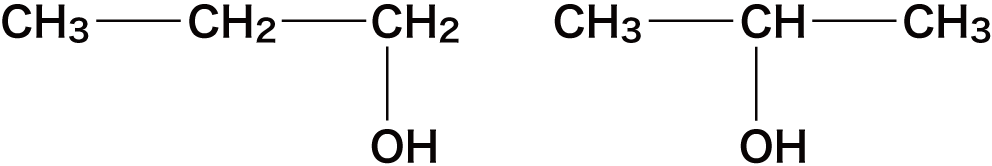
- この例の場合、分子式は同じ(分子を構成している原子やその数は同じ)だが、ヒドロキシ基の付いている位置が異なっている。
異性体の分類
| 構造異性体 | 連鎖異性体/位置異性体/官能基異性体 |
| 立体異性体 | 幾何異性体/光学異性体 |
- 異性体は大きく構造異性体と立体異性体に分類される。
- また、構造異性体は連鎖異性体・位置異性体・官能基異性体に、立体異性体は幾何異性体・光学異性体に分類される。
- これ以降は、これらの異性体について個別に細かく解説する。
構造異性体
- 原子の結合順序が異なる異性体を構造異性体という。
- 構造異性体は連鎖異性体・位置異性体・官能基異性体の3つに分類できる。
連鎖異性体
- 連鎖異性体とは炭素骨格(C原子の並び方)が異なる異性体である。
- 3つほど例を挙げる。
C4

C5
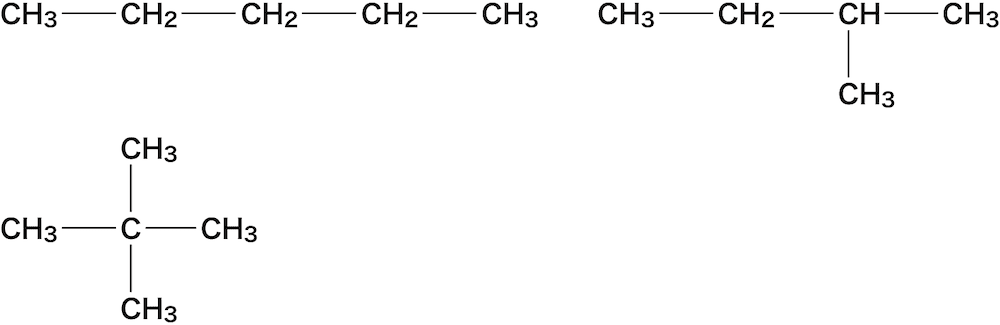
C6

位置異性体
- 官能基の結合している位置が異なる異性体を位置異性体という。
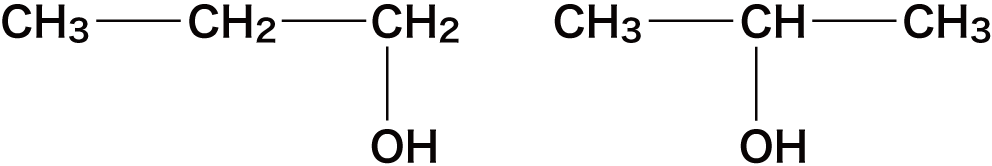
- この例ではヒドロキシ基ーOHの付く位置が異なっている。
官能基異性体
- 官能基の種類が異なる異性体を官能基異性体という。
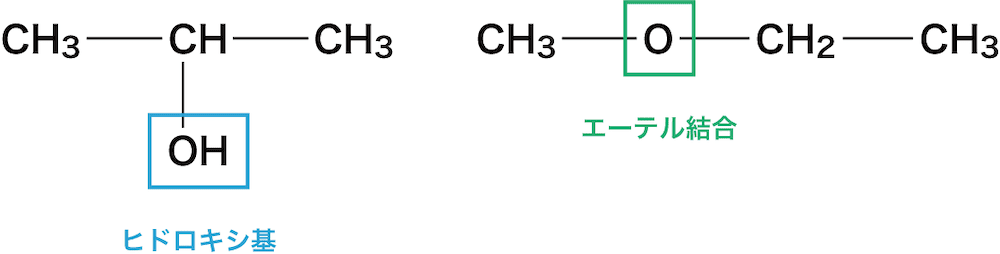
立体異性体
- 構成原子は同じで立体的な位置関係が異なる異性体を立体異性体という。
- 幾何異性体と光学異性体の2種類が存在する。
幾何異性体
- 不飽和結合(C=C結合)は(単結合と異なり)結合を軸にして回転させることができない。

- この性質故に、C=C結合をもつ化合物には幾何異性体(シス-トランス異性体)という異性体が存在する可能性がある。
| 名称 | シスー2ーブテン | トランスー2ーブテン |
| 構造 | 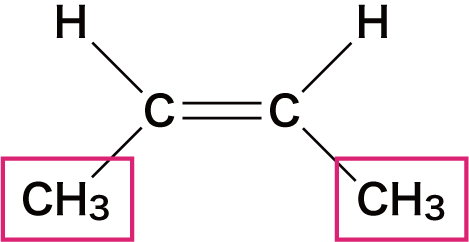 | 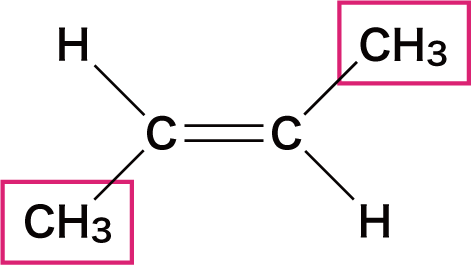 |
- この2つの物質は構成原子は同じだが、メチル基(ーCH3)の位置が異なっている。
- このとき、CーC結合を結ぶ線に対して、同じ原子(原子団)が同じ側にあるとシス型、反対側にあるとトランス型という。
- 左側の「シスー2ーブテン」はCH3が2つとも下側に、「トランスー2ーブテン」はCH3の片方は上側に、もう片方は下側に存在している。
- 先述の通りC=C結合は回転することができないため、シスー2ーブテンの半分がくるっと回ってトランスー2ーブテンになったりということは起こり得ない。
- したがって、この2つは(構成原子とその数が一緒なのにも関わらず同じ物質にはならないので)異性体ということになる。
光学異性体
- ある炭素C原子に異なる4種類の原子や官能基が結合しているとき、これを鏡に映したもの(鏡像体)は重ね合わせることができない(左手と右手のような関係)。
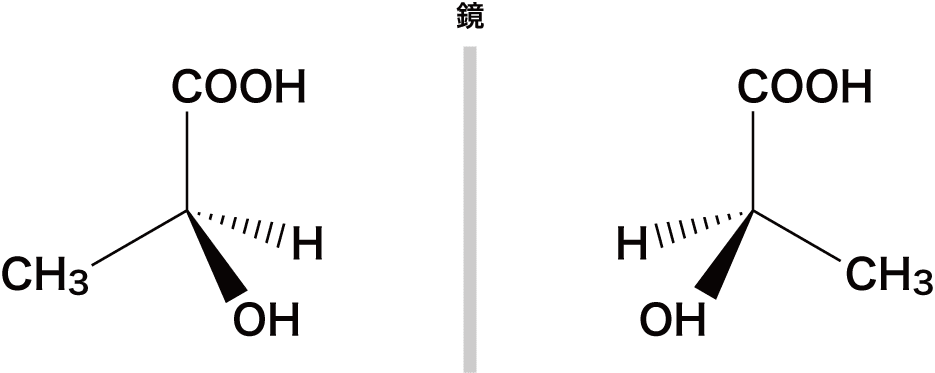
- この重ね合わせることができない物質を光学異性体(=鏡像異性体)という。
- 光学異性体が存在するためには1つ重要な条件がある。
“不斉炭素”が必要
- 光学異性体が存在するためには“不斉炭素原子”が存在する必要がある。
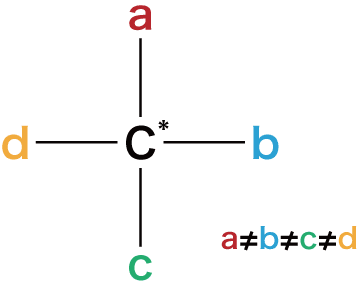
- 不斉炭素原子とは4つの異なる原子(官能基)が結合している炭素C原子のことで、*印を付けてC*と表すことが多い。
- 上で挙げた化合物も、真ん中の炭素が不斉炭素原子になっている。
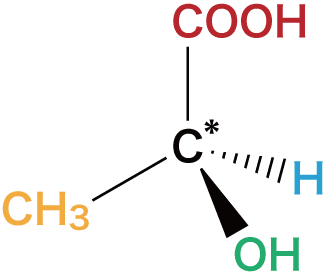
- また、光学異性体の性質について以下の事項を押さえておこう。
- 化学的/物理的性質は同じ
- 旋光性/生理活性は異なる
- 光学異性体は化学的・物理的な性質(反応性・沸点・融点など)はほぼ同じで、旋光性(平面偏光の偏光面を回転させる性質)と生理活性(酵素反応・生体内反応など)が異なる。酵素のところなどでも重要になってくるのでしっかり覚えておこう。
不飽和度と構造異性体
- 分子式から異性体を書くときは、炭素C原子数だけではなく、水素H原子数が重要な情報源となる。
- 例えば、飽和炭化水素が二重結合や環状構造を形成する場合、H原子2つを取り除く必要がある。
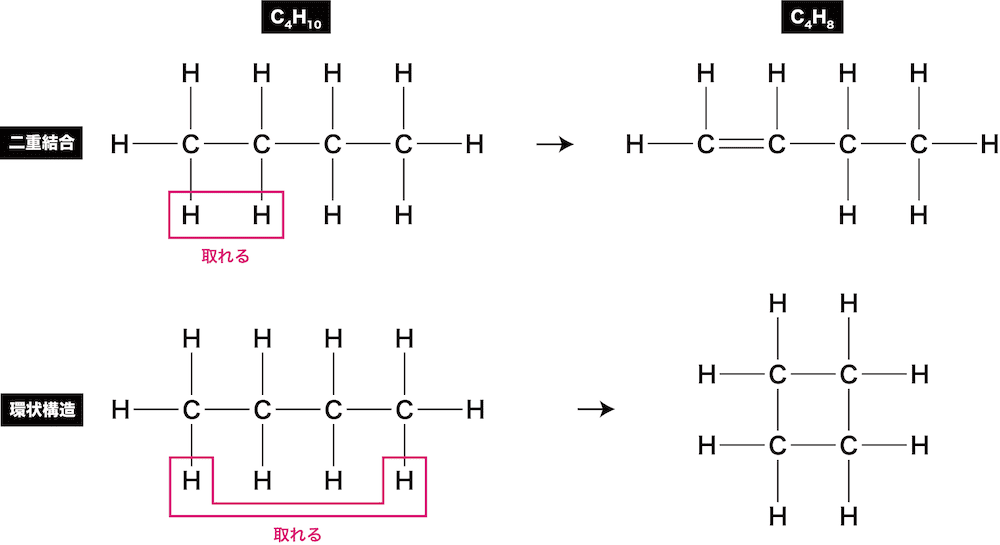
- これは逆に「H原子が飽和炭化水素よりも2個少なければ二重結合又は環状構造が1個ある」と考えることもできる。
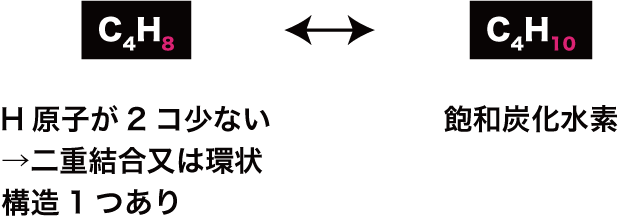
- このように、H原子の不足数を元に有機化合物の構造を推定することができ、それをわかりやすい数字で表したものが不飽和度(水素原子欠乏度)である。
\[ \begin{align} &不飽和度(U)\\
&= \mathrm{\frac{ (H原子の最大数)-(今あるH原子数) }{ 2 }}\end{align} \]
分子式から異性体を書く手順
- 分子式から異性体を書く手順を解説する。
●STEP1
不飽和度(U)を求める。
●STEP2
炭素骨格を考える。
●STEP3
炭素骨格に官能基を組み込む。
- ここでは例として分子式C3H8Oの異性体を書き出す。
STEP
不飽和度(U)を求める
まず、与えられた物質の不飽和度を求める。
\[ \begin{align} U&= \mathrm{\frac{ (H原子の最大数)-(今あるH原子数) }{ 2 }}\\
&= \frac{ (2n+2)-(今ある\mathrm{H}原子数) }{ 2 }\\
&=\frac{ 2×3+2-8 }{ 2 }\\
&=0
\end{align} \]
不飽和度が0になったのでこの有機化合物は”鎖式飽和”だとわかる。
STEP
炭素骨格を考える
次に、炭素骨格を考える。
今回は炭素数3であり、STEP1より”鎖式飽和”のため、炭素骨格は次の1パターンのみである。
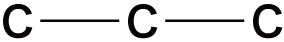
※以下の形を2パターン目として数えてしまう人が多い。

しかし、この形は折れ曲がっている炭素を伸ばせば同じ形になる。
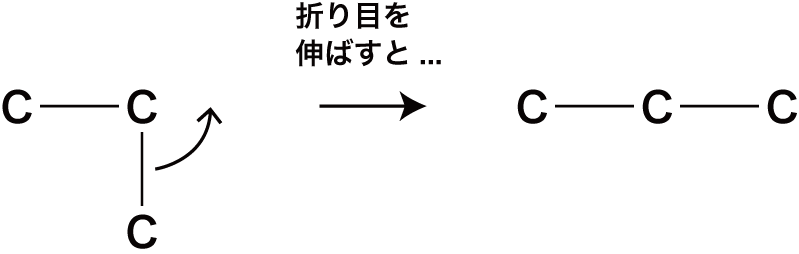
STEP
炭素骨格に官能基を組み込む
最後に、炭素骨格に官能基を組み込んでいく。
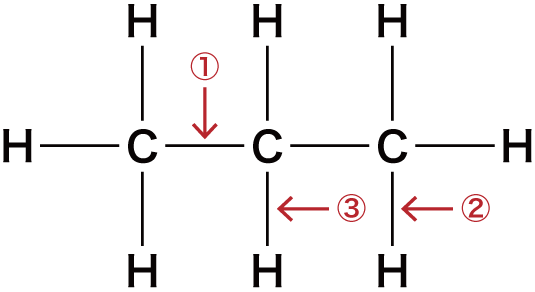
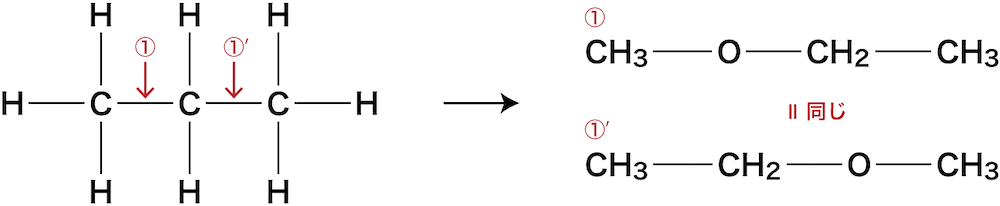
① C-Cの間にOを入れる
C-Cの間である①の箇所にOを入れると次のようになる。
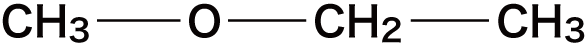
ちなみに下図①’の位置にOを入れたくなるかもしれないが、①に入れた場合と同じ化合物になってしまうのでダメ(ひっくり返すと同じ)。
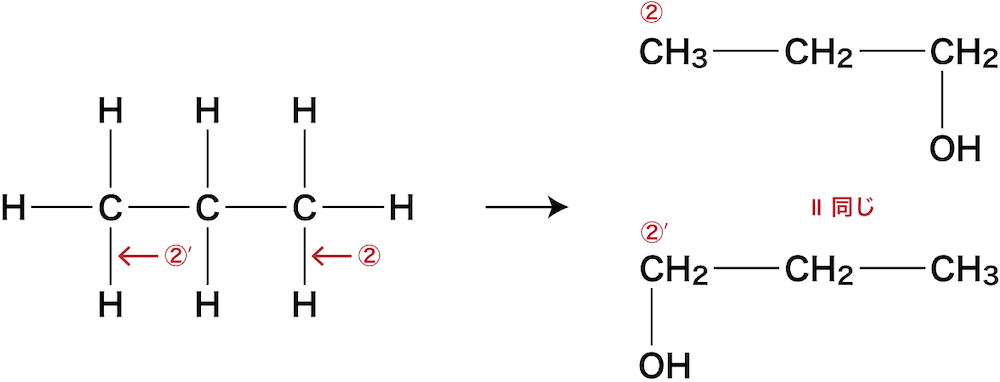
②③ C-Hの間にOを入れる
C-Hの間である②及び③の箇所にOを入れると次のようになる。
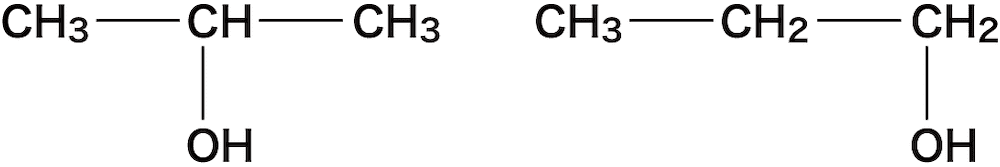
下図②’の位置にOを入れると②に入れた場合と同じ化合物(②’)になってしまうのでダメ(ひっくり返すと同じ)。