MENU
不飽和度(公式、計算解法、窒素を含む場合など)
はじめに
【プロ講師解説】このページでは『不飽和度(公式、計算解法、窒素を含む場合など)』について解説しています。
不飽和度の公式
- 不飽和度の公式は次の通りである。
\[ \begin{align} &不飽和度(U)\\
&= \mathrm{\frac{ (H原子の最大数)-(今あるH原子数) }{ 2 }}\end{align} \]
- 不飽和度は水素H原子の最大数から今あるH原子の数を引き、それを2で割ることで求めることができる。
炭化水素の不飽和度
- 炭化水素はCとHのみからなる有機化合物である。
- 鎖式飽和炭化水素(炭化水素のうちH原子の不足がなく直鎖状のもの)では、各C原子に上下2個のH原子が付いている。
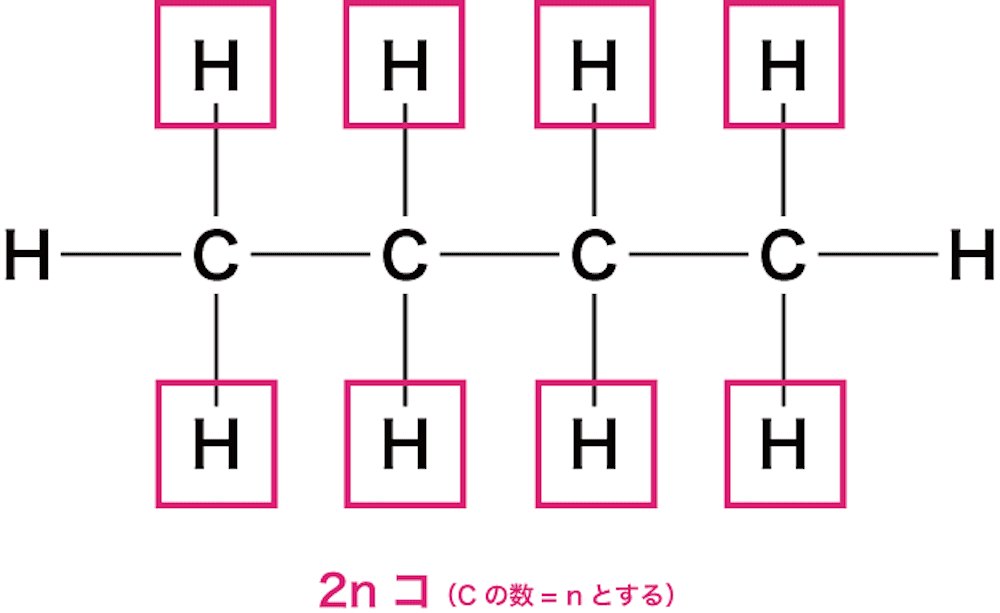
- また、両端のC原子にはさらに1個ずつH原子が付いている。
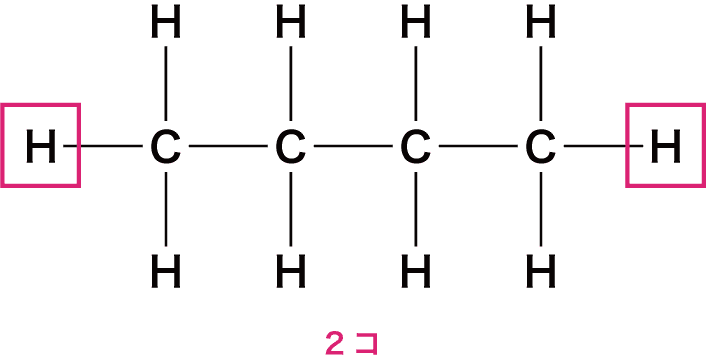
- したがって、H原子の最大数は(2n+2)個である。
ex)C4H10の不飽和度
\[ \begin{align} U&= \mathrm{\frac{ (H原子の最大数)-(今あるH原子数) }{ 2 }}\\
&= \frac{ (2n+2)-(今ある\mathrm{H}原子数) }{ 2 }\\
&=\frac{ (2×4+2)-10 }{ 2 }\\
&=0
\end{align} \]
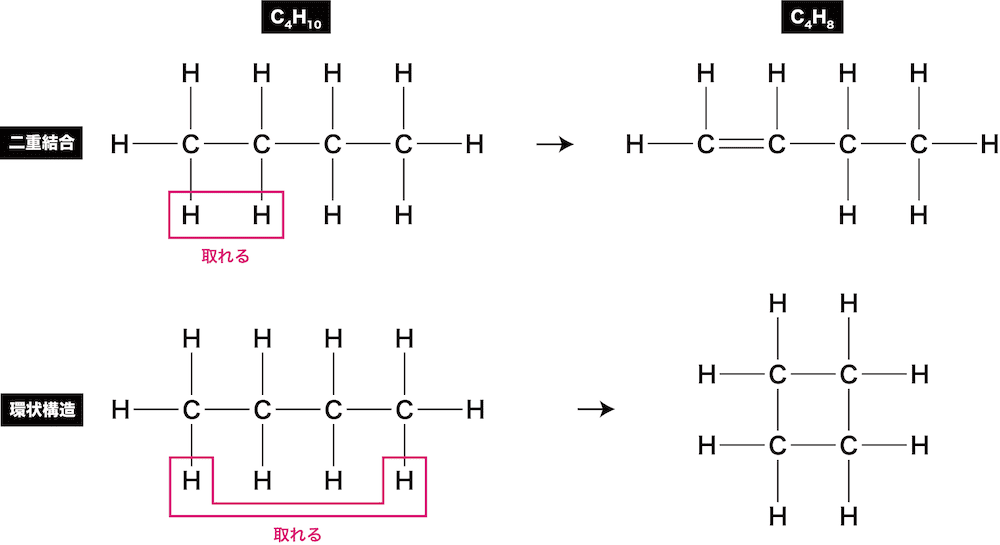
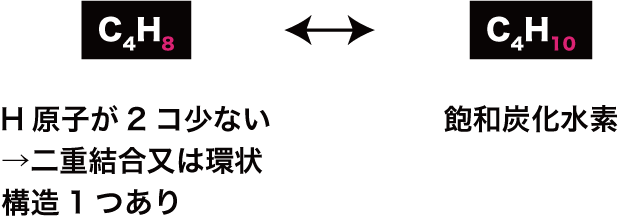
ex)C4H8の不飽和度
\[ \begin{align} U&= \mathrm{\frac{ (H原子の最大数)-(今あるH原子数) }{ 2 }}\\
&= \frac{ (2n+2)-(今ある\mathrm{H}原子数) }{ 2 }\\
&=\frac{ 2×4+2-8 }{ 2 }\\
&=1
\end{align} \]
O原子を含む場合の不飽和度
- 酸素O原子が1個入っても、H原子の最大数には影響しない。
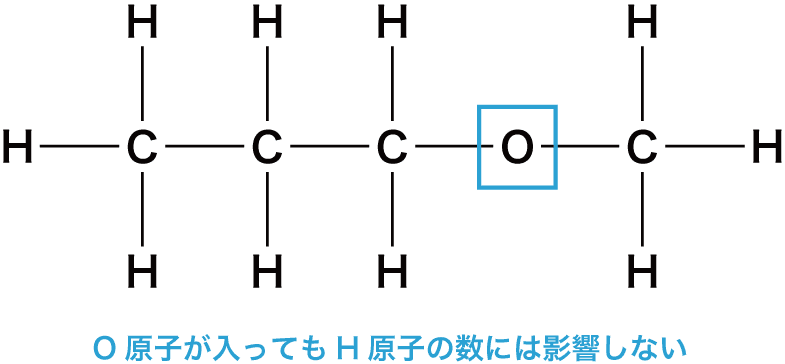
- したがって、H原子の最大数は(2n+2)個である。
ex)C4H10Oの不飽和度
\[ \begin{align} U&= \mathrm{\frac{ (H原子の最大数)-(今あるH原子数) }{ 2 }}\\
&= \frac{ (2n+2)-(今ある\mathrm{H}原子数) }{ 2 }\\
&=\frac{ 2×4+2-10 }{ 2 }\\
&=0
\end{align} \]
ex)C4H8O2の不飽和度
\[ \begin{align} U&=\mathrm{ \frac{ (H原子の最大数)-(今あるH原子数) }{ 2 }}\\
&= \frac{ (2n+2)-(今ある\mathrm{H}原子数) }{ 2 }\\
&=\frac{ 2×4+2-8 }{ 2 }\\
&=1
\end{align} \]
N原子を含む場合の不飽和度
- 窒素N原子が1個入ると、H原子の最大数は1個増加する。
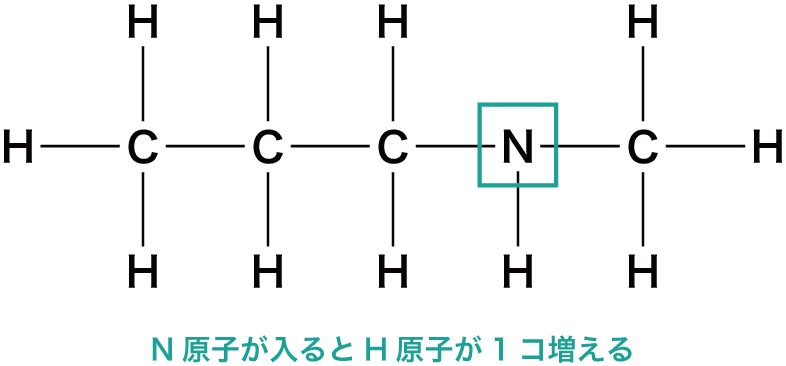
- したがって、H原子の最大数は(2n+2+N原子数)個である。
ex)C4H9NO2の不飽和度
\[ \begin{align} U&= \mathrm{\frac{ (H原子の最大数)-(今あるH原子数) }{ 2 }}\\
&=\frac{ (2×4+2+1)-9 }{ 2 }\\
&=1
\end{align} \]
ハロゲンを含む場合の不飽和度
- ハロゲンである塩素Cl原子が1個入ると、H原子の最大数は1個減少する。
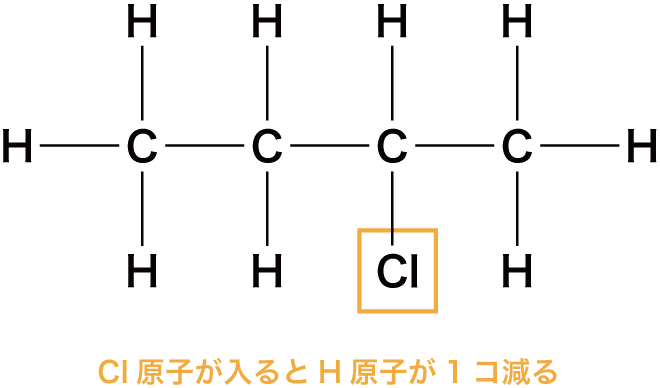
- したがって、H原子の最大数は(2n+2ーハロゲン原子数)個である。
ex)C4H9Clの不飽和度
\[ \begin{align} U&= \mathrm{\frac{ (H原子の最大数)-(今あるH原子数) }{ 2 }}\\
&=\frac{ (2×4+2-1)-9 }{ 2 }\\
&=0
\end{align} \]
- ハロゲンについて詳しくは次のページを参照のこと。