【高校】ミカエリス・メンテン式を攻略！酵素反応速度論/ミカエリス定数の導出など

反応速度

• 酵素（一覧・酵素基質複合体・基質特異性・最適温度・最適pHなど）にあるように、酵素反応は次の二段階で進行する。

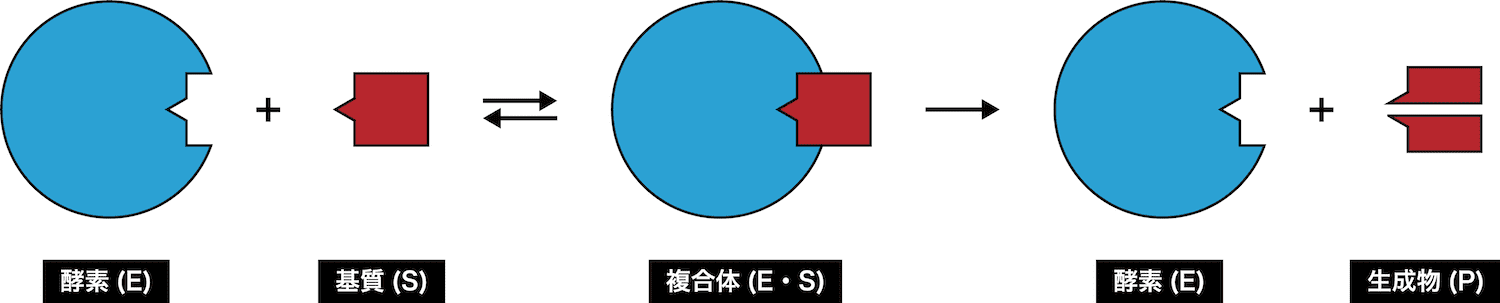
• これに基づいて、酵素反応の速度式を導く。
• 酵素(E)、基質(S)、酵素-基質複合体(ES)、生成物(P)が絡む各反応の速度定数をk₁、k_-1、k₂とする。

\[ \begin{align}&\mathrm{E + S} \underset{k_{-1}}{\overset{k_{1}}{\rightleftarrows}} \mathrm{ES・・・①}\\
&\mathrm{ES} \overset{k_{2}}{\rightarrow} \mathrm{E + P・・・②} \end{align}\]

• 酵素(E)、基質(S)、酵素-基質複合体(ES)、生成物(P)の濃度をそれぞれ[E]、[S]、[ES]、[P]とする。
• ①におけるESの生成速度v₁は次のようになる。

\[v_{1}=k_{1}\mathrm{[E][S]} \]

• ①におけるESの分解速度v_-1は次のようになる。

\[ v_{-1}=k_{-1}\mathrm{[ES]} \]

• ②におけるESの分解速度v₂は次のようになる。

\[ v_{2}=k_{2}\mathrm{[ES]} \]

• よってESの分解の合計速度v₃は次のようになる。

\[ v_{3}=v_{-1}+v_{2}=k_{-1}\mathrm{[ES]}+k_{2}\mathrm{[ES]}=(k_{-1}+k_{2})\mathrm{[ES]} \]

• 「酵素」には基質と結合していない状態のEと結合している状態のESがあるから全酵素濃度を[E_{T}]とすると、次のようになる。

\[\mathrm{ [E_{T}]=[E]+[ES]・・・③ }\]

• 多くの酵素反応では①の平衡には瞬時に達する（単純にくっつくか離れるかだけの話なので）。
• 一方、②の反応は①に比べてかなり遅く、いわゆる律速段階となる。

• 通常、酵素反応は[E]<<[S]の条件で行う（触媒である酵素Eは少量で良い）ため、ESがE+Pに変化してもEは瞬時に過剰のSと反応してESとなる。
• したがって、Sが過剰のとき、[ES]は一定となる（定常状態：ESの生成と分解がつり合う状態）。
• このとき、v₁=v₃なので…

\[ k_{1}\mathrm{[E][S]}=(k_{-1}+k_{2})\mathrm{[ES]・・・④} \]

• ③と④から[E]を消去して、[ES]について解く。④より…

\[\mathrm{ [E]=}\frac{ (k_{-1}+k_{2})\mathrm{[ES]} }{ k_{1}\mathrm{[S]} } \]

• これを③に代入すると次のようになる。

\[ \begin{align}
\mathrm{[E_{T}]}&=\frac{ (k_{-1}+k_{2})\mathrm{[ES]} }{ k_{1}\mathrm{[S]} }+\mathrm{[ES]} \\
&=\Biggl( \frac{ k_{-1}+k_{2}\mathrm{[ES]} }{ k_{1}\mathrm{[S]} }+1\mathrm{[ES]} \Biggr) \\
&=\frac{ k_{-1}+k_{2}+k_{1}\mathrm{[S]} }{ k_{1}\mathrm{[S]} }\mathrm{[ES]}
\end{align} \]

• よって…

\[ \begin{align}
\mathrm{[ES]}&=\frac{ k_{1}\mathrm{[S][E_{T}]} }{ k_{-1}+k_{2}+k_{1}\mathrm{[S]} } \\
&= \frac{ \mathrm{[S][E_{T}]} }{ \frac{ k_{-1}+k_{2} }{ k_{1} }+\mathrm{[S]} }\\
&=\frac{\mathrm{ [S][E_{T}] }}{ K_{m}+\mathrm{[S]} }\Biggl(ミカエリス定数K_{m=} \frac{ k_{-1}+k_{2} }{ k_{1} } \Biggr)
\end{align} \]

• 以上より、Pの生成速度v₂は次のようになる。

\[ v_{2}=k_{2}\mathrm{[ES]}=\frac{ k_{2}\mathrm{[S][E_{T}]} }{ K_{m}+\mathrm{[S]} } \]

• また、[E]<<[S]のとき、全ての酵素Eが基質Sと結合し、酵素-基質複合体ESをつくっている。つまり、すべての酵素EがPの生成に関与している。
• このとき、[ES]=[E_T]が成立し、生成物Pの生成速度は最大値v_maxになる。
• よって、v₂=k₂[ES] より…

\[ \begin{align}v_{max}&=k_{2}\mathrm{[E_{T}]}\\
\therefore v_{2}&=\frac{ k_{2}\mathrm{[S][E_{T}]} }{ K_{m}+\mathrm{[S]} }\\
&=\frac{ v_{max}\mathrm{[S]} }{ K_{m}+\mathrm{[S]} } (ミカエリス・メンテンの式)
\end{align} \]

• これがミカエリス・メンテン式である。
• 以下、ミカエリス・メンテンの式及びミカエリス定数についてさらに詳しく解説する。

[S]がK_mよりも十分に小さいとき

• [S]<<K_mよりK_m+[S]≒K_mなので…

\[ \begin{align} v_{2}&=\frac{ v_{max}\mathrm{[S]} }{ K_{m}+\mathrm{[S]} }\\
&≒\frac{ v_{max} }{ K_{m} }\mathrm{[S]}
\end{align} \]

• よって、v₂は[S]に比例する。

[S]がK_mよりも十分に大きいとき

• [S]>>K_mよりK_m+[S]≒[S]なので…

\[ \begin{align} v_{2}&=\frac{ v_{max}\mathrm{[S]} }{ K_{m}+\mathrm{[S]} }\\
&≒\frac{ v_{max}\mathrm{[S]} }{\mathrm{ [S]} }\\
&=v_{max}
\end{align} \]

• よって、v₂は[S]によらず一定（最大値）となる。

[S]=K_mのとき

\[ \begin{align} v_{2}&=\frac{ v_{max}\mathrm{[S]} }{ K_{m}+\mathrm{[S]} }\\
&≒\frac{ v_{max}K_{m} }{ K_{m}+K_{m} }\\
&=\frac{ v_{max} }{ 2 }
\end{align} \]

• 普通k₂はk₁、k_-1よりも十分小さいから…

\[ \begin{align} K_{m}&=\frac{ k_{-1}+k_{2} }{ k_{1} }\\
&≒\frac{ k_{-1} }{ k_{1} }
\end{align} \]

• 一方…

\[ \mathrm{E + S} \underset{k_{-1}}{\overset{k_{1}}{\rightleftarrows}} \mathrm{ES} \]

• 上式において、ESの解離平衡定数をK_sとすると…

\[ \begin{align} K_{s}&=\frac{\mathrm{ [E][S]} }{\mathrm{ [ES]} }\\
&≒\frac{ k_{-1} }{ k_{1} }（\because v_{1}=v_{-1}よりk_{1}\mathrm{[E][S]}=k_{-1}\mathrm{[ES]}）
\end{align} \]

• よって…

\[ K_{m}≒K_{s} \]

• 最後の式（K_m≒K_s）から分かるのは、ミカエリス定数K_mの大きさと複合体ESの解離しやすさは一致するということである。
• 複合体ESが酵素Eと基質Sに解離してしまうと、その分生成物Pが生じなくなる。つまり、ミカエリス定数K_mの大きさは酵素の触媒能力の指標になる。
• 結論、K_mが小さいほど基質Sとの親和性が高く、触媒能力が高い酵素であるということである。