【プロ講師解説】このページでは『飽和蒸気圧（定義・性質・グラフ・計算問題の解法など）』について解説しています。解説は高校化学・化学基礎を扱うウェブメディア『化学のグルメ』を通じて6年間大学受験に携わるプロの化学講師が執筆します。
飽和蒸気圧とは
密閉容器に液体を入れて十分時間が経つと「液体が気体になる量」と「気体が再び液体に戻る量」が一定となり、見かけ上、容器内の気体分子数に変化がなくなる。（気液平衡）
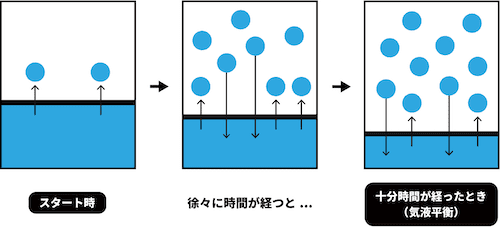
このとき、温度と体積が一定であると仮定すると、モル数に変化はないので圧力も一定となる。
P
=
\underbrace{ \frac{ nRT }{ V } }
_{ \text{ 一定 }}
\]
このときの圧力を、この温度におけるその物質の飽和蒸気圧（または蒸気圧）という。
※PV=nRTは気体の状態方程式と呼ばれる式である。
気体の状態方程式について詳しくは気体の状態方程式（単位・導出・計算問題の解き方など）を確認しよう。
飽和蒸気圧の性質
| NO.1 | 物質の種類と温度に依存する |
| NO.2 | 容器の大きさや他の気体の存在は関係ない |
体積一定で温度を上げていくと、気体は徐々に蒸発し、気相中に存在する気体のmol数が増える。これに伴い圧力（飽和蒸気圧）が増加する。
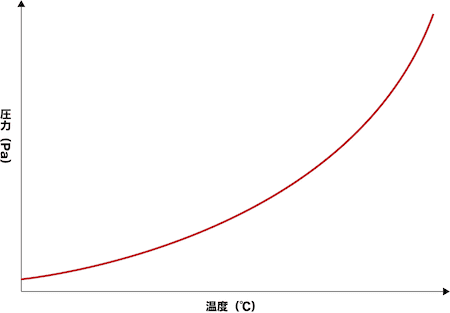
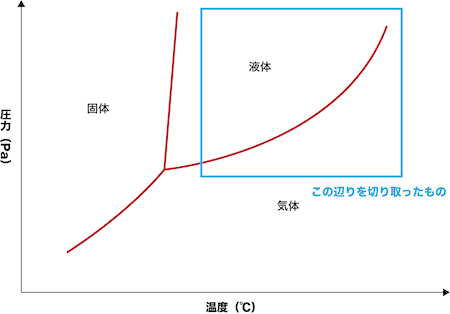
ちなみにこのような圧力（飽和蒸気圧）と温度の関係を表す曲線を蒸気圧曲線といい、状態図の一部を切り取ったものである。
飽和蒸気圧が絡んだ計算問題
飽和蒸気圧の計算問題を解く前に以下のことを押さえておく必要がある。
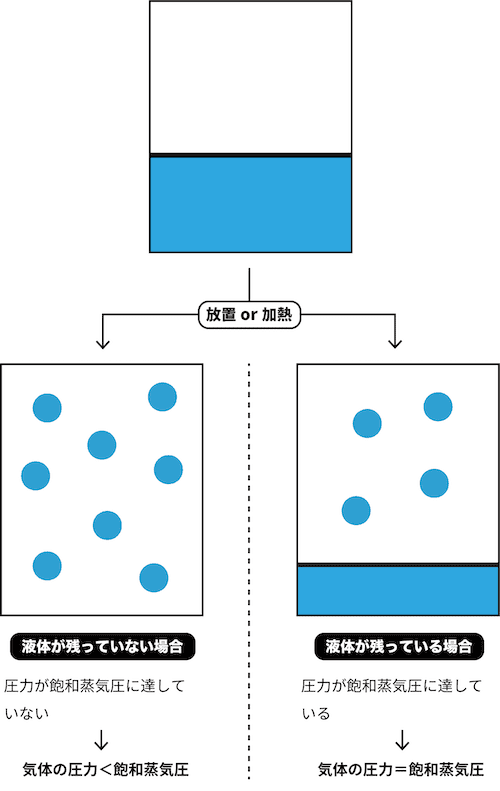
密閉容器に液体を入れて放置（or加熱）したとき、液体が残らない場合（パターン１）と残る場合（パターン２）がある。
パターン１では容器内の気体の圧力が飽和蒸気圧に達しておらず「気体の圧力＜飽和蒸気圧」の状態である。一方、パターン２では容器内の気体の圧力が飽和蒸気圧に達しており「気体の圧力＝飽和蒸気圧」の状態である。
それではこれから飽和蒸気圧が絡んだ計算問題を３パターン紹介していく。いずれも入試頻出問題なのでしっかり解けるようになろう！
【パターン１】状態判定
| STEP1 | 液体全てが気体になったと仮定し、気体の状態方程式を用いて“仮の圧力”を求める |
| STEP2 | STEP1で求めた圧力P仮と飽和蒸気圧を比較
P仮 ＞ 飽和蒸気圧 → 液化している |
容器に液体を入れてしばらく放置（or加熱）した後、入れた液体が全て気体になっているのか、それとも一部が液体として存在しているのかを判断する問題である。
上の2STEPを用いて次の問題を解いてみよう。
問題
STEP1
まずは、液体が全て気体になったと仮定し、気体の状態方程式を用いて「仮の圧力」を求める。
\begin{align} PV&=nRT\\
\leftrightarrow P&=\frac{ nRT }{ V }\\
&=\frac{ \frac{ 0.90(g) }{ 18(g/mol) }×8.3×10^{3}(L・Pa/(K・mol))×(80+273)(K) }{ 2.0(L) }\\
&≒7.3×10^{4}(Pa) \end{align}
\]
STEP2
次に、STEP1で求めた圧力P仮と飽和蒸気圧を比較する。
問題文に80℃における水の飽和蒸気圧は4.7×104(Pa)と書いてあるので、
\underbrace{ 7.3×10^{4}(Pa) }_{ \text{ STEP1で求めた圧力 }}>\underbrace{ 4.7×10^{4}(Pa) }_{ \text{ 飽和蒸気圧 }}
\]
今回はSTEP1で求めた仮の圧力が飽和蒸気圧を上回っているので、「液化している」と判断できる。
【パターン２】圧力及び液化している分の質量を求める問題
| STEP1 | 液体全てが気体になったと仮定し、気体の状態方程式を用いて“仮の圧力”を求める |
| STEP2 | STEP1で求めた圧力P仮と飽和蒸気圧を比較
P仮 ＞ 飽和蒸気圧 → 液化している |
| STEP3 | 最初に入れたgに \[ \frac{ P_{仮}-P_{飽} }{ P_{仮} }\\ \] を掛け、液化しているgを出す |
このタイプの問題は上のSTEPを使って解く。次の例題で説明していこう。
問題
STEP1
まずは、液体が全て気体になったと仮定し、気体の状態方程式を用いて「仮の圧力」を求める。
\begin{align} PV&=nRT\\
\leftrightarrow P&=\frac{ nRT }{ V }\\
&=\frac{ \frac{ 1.8(g) }{ 18(g/mol) }×8.3×10^{3}(L・Pa/(K・mol))×(80+273)(K) }{ 3.0(L) }\\
&≒9.8×10^{4}(Pa) \end{align}
\]
STEP2
次に、STEP1で求めた圧力（P仮）と飽和蒸気圧を比較する。
\underbrace{ 9.8×10^{4}(Pa) }_{ \text{ STEP1で求めた圧力 }}>\underbrace{ 4.7×10^{4}(Pa) }_{ \text{ 飽和蒸気圧 }}
\]
仮の圧力が飽和蒸気圧を上回っているので、気体の一部は液化しており容器内の気体の圧力は飽和蒸気圧（4.7×104Pa）になっていると考えられる。
STEP3
最後に、最初に入れたgに「(P仮ーP飽)/P仮」をかけ、液化しているgを出す。
\begin{align}&1.8(g)×\frac{ 9.8×10^{4}(Pa)-4.7×10^{4}(Pa) }{ 9.8×10^{4}(Pa) }\\
&≒0.94(g)\end{align}
\]
【パターン３】燃焼&冷却後の気体の分圧・全圧を求める問題
| STEP1 | 反応量シートを用いて燃焼後の各気体の分圧を出す（分圧が飽和蒸気圧を超えている場合はその気体の圧力は飽和蒸気圧として考える） |
| STEP2 | 分圧を足し合わせ、全圧を求める |
このタイプの問題は上のSTEPを使って解く。次の例題で説明していこう。
問題
STEP1
まずは、反応量シートを用いて燃焼後の各気体の分圧を出す。
このとき、分圧が飽和蒸気圧を超えている場合、その気体の圧力は飽和蒸気圧として考える。
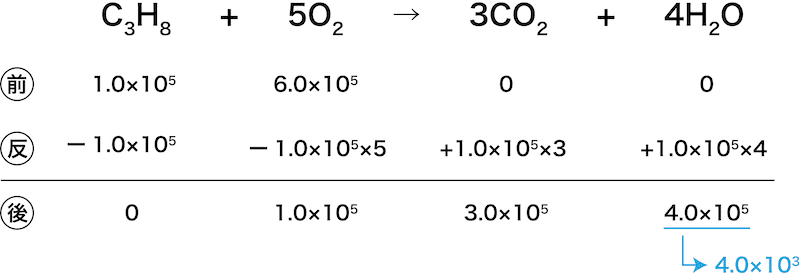
今回は問題文中にH2Oの飽和蒸気圧が4.0×103Paと書いてあるので、計算上4.0×105Paと出たH2Oの分圧は4.0×103Paまで低下させる。（はみ出た分は“液化”している）
STEP2
次に、分圧を足し合わせることで全圧を求める。
\begin{align}P_{全}&=P_{O_{2}}+P_{CO_{2}}+P_{H_{2}O}\\
&=1.0×10^{5}+3.0×10^{5}+4.0×10^{3}\\
&=4.04×10^{5}\\
&≒4.0×10^{5}(Pa)\end{align}
\]
飽和蒸気圧に関する演習問題
問１
密閉容器に液体を入れて十分時間が経つと「液体が気体になる量」と「気体が再び液体に戻る量」が一定となり、見かけ上、容器内の気体分子数に変化がなくなる。この状態を【１】という。
密閉容器に液体を入れて十分時間が経つと「液体が気体になる量」と「気体が再び液体に戻る量」が一定となり、見かけ上、容器内の気体分子数に変化がなくなる。これを気液平衡という。
問２
気液平衡時、温度と体積が一定であると仮定すると、モル数に変化はないので圧力も一定となる。このときの圧力をこの温度におけるその物質の【１】という。
密閉容器に液体を入れて十分時間が経つと「液体が気体になる量」と「気体が再び液体に戻る量」が一定となり、見かけ上、容器内の気体分子数に変化がなくなる。（気液平衡）
このとき、温度と体積が一定であると仮定すると、モル数に変化はないので圧力も一定となる。
P
=
\underbrace{ \frac{ nRT }{ V } }
_{ \text{ 一定 }}
\]
このときの圧力を、この温度におけるその物質の飽和蒸気圧（または蒸気圧）という。
※PV=nRTは気体の状態方程式と呼ばれる式である。
気体の状態方程式について詳しくは気体の状態方程式（単位・導出・計算問題の解き方など）を確認しよう。
問３
体積一定で温度を上げていくと、気体は徐々に蒸発し、気相中に存在する気体のmol数が増える。これに伴い圧力（飽和蒸気圧）が増加する。このときの圧力（飽和蒸気圧）と温度の関係を表す曲線を【１】といい、これは【２】の一部を切り取ったものである。
体積一定で温度を上げていくと、気体は徐々に蒸発し、気相中に存在する気体のmol数が増える。これに伴い圧力（飽和蒸気圧）が増加する。
ちなみにこのような圧力（飽和蒸気圧）と温度の関係を表す曲線を蒸気圧曲線といい、状態図の一部を切り取ったものである。
※状態図について詳しくは物質の三態と状態図を参照
関連：計算ドリル、作りました。
化学のグルメオリジナル計算問題集「理論化学ドリルシリーズ」を作成しました！モル計算や濃度計算、反応速度計算など入試頻出の計算問題を一通りマスターできるシリーズとなっています。詳細は【公式】理論化学ドリルシリーズにて！
・化学のグルメ運営代表
・高校化学講師
・薬剤師
・デザイナー/イラストレーター
数百名の個別指導経験あり（過去生徒合格実績：東京大・京都大・東工大・東北大・筑波大・千葉大・早稲田大・慶應義塾大・東京理科大・上智大・明治大など）
2014年よりwebメディア『化学のグルメ』を運営
公式オンラインストアで販売中の理論化学ドリルシリーズ・有機化学ドリル等を執筆
著者紹介詳細