MENU
溶解度積(計算問題・単位・溶解度との関係・沈殿生成判定など)
はじめに
【プロ講師解説】このページでは『溶解度積(計算問題・単位・溶解度との関係・沈殿生成判定など)』について解説しています。
溶解度積とは
- 水に溶けにくい電解質MmAaは飽和溶液中で次のような平衡状態になっている。
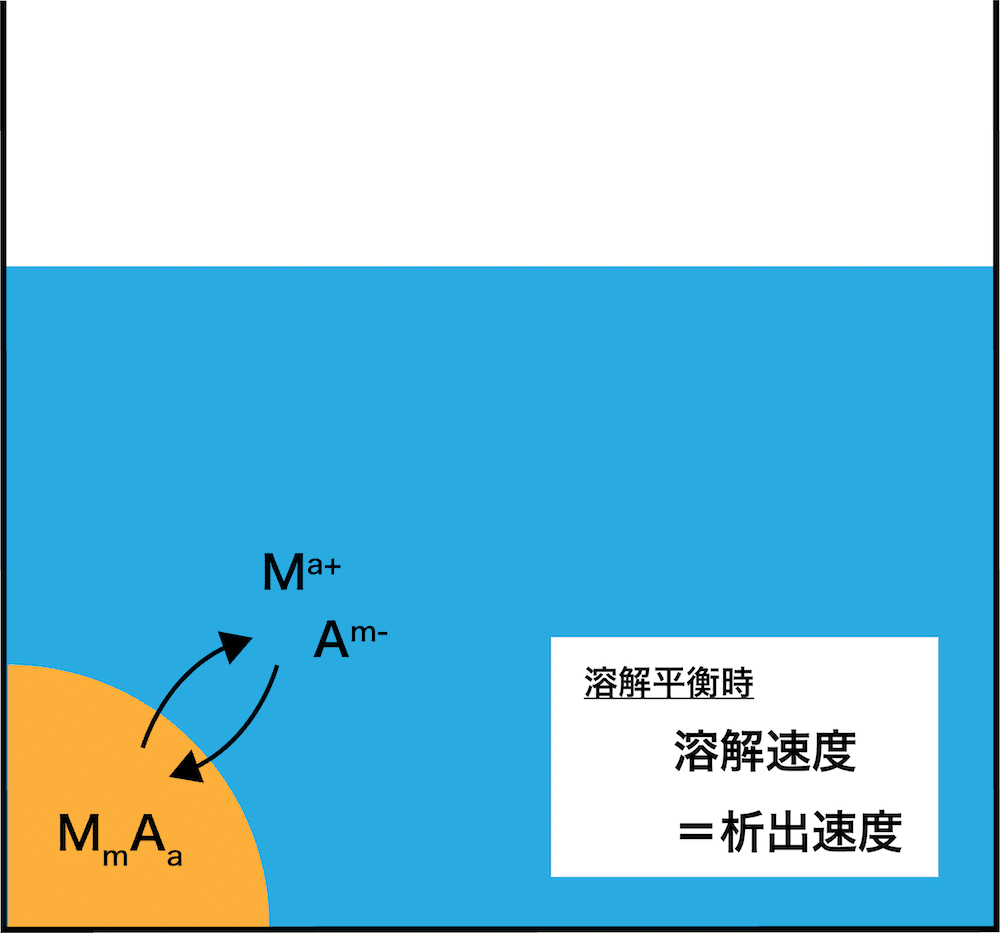
\[ \mathrm{M_{m}A_{a}(固) ⇆ mM^{a+} + aA^{m-}} \]
- このとき、次の式が成り立つ。
\[ K = \mathrm{\frac{ [M^{a+}]^{m}[A^{m-}]^{a} }{ [M_{m}A_{a}(固)] } }\]
- MmAaは固体のため[MmAa(固)]は一定とみなすことができる。したがって、[MmAa(固)]を移項すると、次のようになる。
\[ \underbrace{\mathrm{[M_{m}A_{a}(固)]}×K}_{ 一定 } =\mathrm{[M^{a+}]^{m}[A^{m-}]^{a}} \]
- ここで、定数(一定)である[MmAa(固)]×Kを改めてKspと定義する。
\[ K_{sp} =\mathrm{[M^{a+}]^{m}[A^{m-}]^{a} }\]
- このKspを溶解度積という。
塩化銀AgClの溶解度積
- ちなみに、テスト頻出の「塩化銀AgCl」の溶解度積は次のように導くことができる。
- 塩化銀AgClを水に溶解させると一部のAgClが溶け残った水溶液ができ、溶解平衡の状態に達した。この溶解平衡の平衡定数K(AgCl)は次のように表される。
\[ K(\mathrm{AgCl})=\mathrm{\frac{ [Ag^{+}][Cl^{-}] }{ [AgCl(固)] } }\]
- [AgCl(固)]を一定とみなし新しい定数としてKsp(AgCl)を次のように定義する。
\[ K_{\mathrm{sp}}(\mathrm{AgCl})=\mathrm{[Ag^{+}][Cl^{-}] }\]
- このKsp(AgCl)が塩化銀の溶解度積となる。
溶解度積の計算問題
- 溶解度積に関する問題として、テストで頻出の「溶解度積を使って溶解度を求める問題」と「溶解度積を使って沈殿生成の有無を判定する問題」の解き方を解説する。
溶解度積を使って溶解度を求める問題
塩化銀AgClの溶解度を求めよ。ただし、AgClの溶解度積は4.0×10ー10(mol/L)2とする。
- 溶けるAgClをx(mol/L)とすると、Ag+、Cl–の濃度はどちらもx(mol/L)となる。
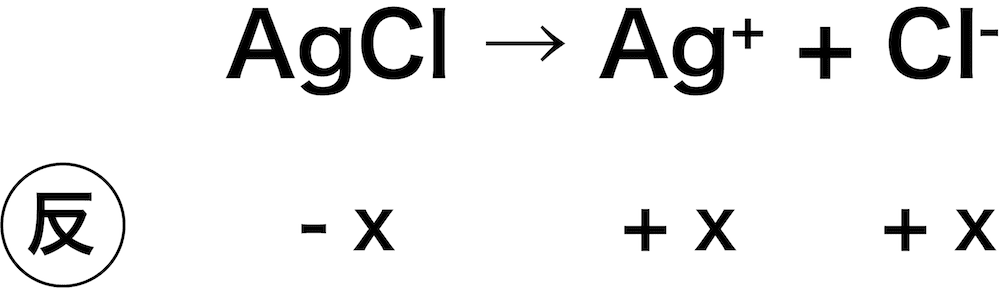
- したがって、次のような式を立てることができる。
\[ \begin{align}&K_{\mathrm{sp}}(\mathrm{AgCl}) = \mathrm{[Ag^{+}][Cl^{-}]}\\
&\leftrightarrow 4.0×10^{-10} = x × x\\
&\therefore x = 2.0×10^{-5}(\mathrm{mol/L})\end{align} \]
Ag2CrO4の溶解度を求めよ。ただし、Ag2CrO4の溶解度積は3.2×10ー11(mol/L)3とする。
- 溶けるAg2CrO4をx(mol/L)とすると、Ag+の濃度は2x(mol/L)、CrO42ーの濃度はx(mol/L)となる。
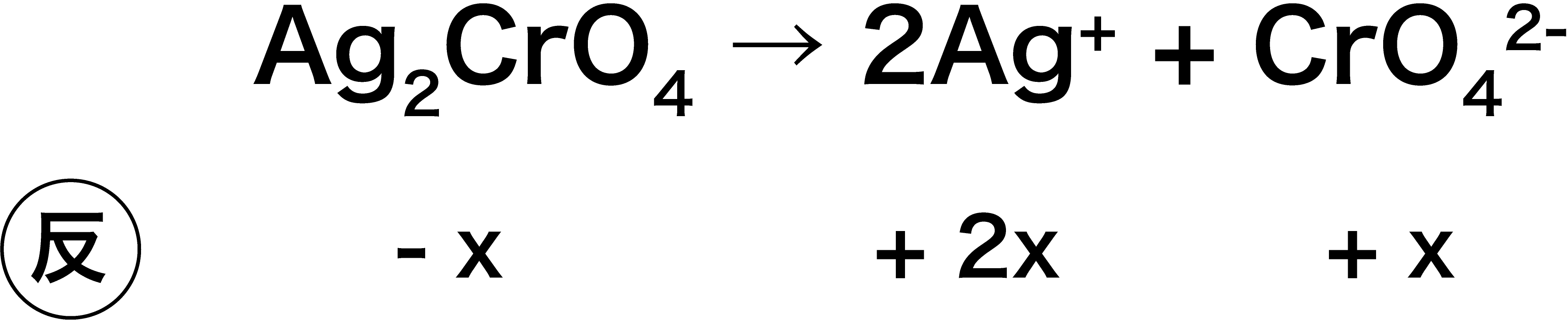
- したがって、次のような式を立てることができる。
\[ \begin{align}&K_{\mathrm{sp}}(\mathrm{Ag_{2}CrO_{4}}) = \mathrm{[Ag^{+}]^{2}[CrO_{4}^{2-}]}\\
&\leftrightarrow 3.2×10^{-11} = (2x)^{2} × x\\
&\therefore x = 2.0×10^{-4}(\mathrm{mol/L}) \end{align}\]
溶解度積を使って沈殿生成の有無を判定する問題
Ag+の濃度が4.0×10ー5mol/L、Clーの濃度が5.0×10ー6mol/Lのとき、沈殿が生成するか判断せよ。AgClの溶解度積は1.8×10ー10(mol/L)2とする。
- 溶解度積を使った沈殿生成判定は次の2STEPで行う。
●STEP1
仮の溶解度積(\(\widetilde{ K_{\mathrm{sp}} }\))を求める。
●STEP2
\(\widetilde{ K_{\mathrm{sp}} }\)と溶解度積(\(K_{\mathrm{sp}}\))を比較する。
\(\widetilde{ K_{\mathrm{sp}} }\)>\(K_{\mathrm{sp}}\) 沈殿が生成
\(\widetilde{ K_{\mathrm{sp}} }\)=\(K_{\mathrm{sp}}\) 沈殿は生成しない
\(\widetilde{ K_{\mathrm{sp}} }\)<\(K_{\mathrm{sp}}\) 沈殿は生成しない
まずは、仮の溶解度積(\(\widetilde{ K_{\mathrm{sp}} }\))を求める。
\[ \begin{align} 仮の溶解度積(\widetilde{ K_{\mathrm{sp}} }) &=\mathrm{[Ag^{+}][Cl^{-}]}\\
&=4.0×10^{-5}×5.0×10^{-6}\\
&=2.0×10^{-10}(\mathrm{mol/L})^{2} \end{align} \]
次に、\(\widetilde{ K_{\mathrm{sp}} }\)と溶解度積(\(K_{\mathrm{sp}}\))を比較し、沈殿生成の有無を決定する。
| \(\widetilde{ K_{\mathrm{sp}} }\)と\(K_{\mathrm{sp}}\)の比較 | 沈殿 |
|---|---|
| 仮の溶解度積>溶解度積 | 生成する |
| 仮の溶解度積=溶解度積 | (ギリ)生成しない |
| 仮の溶解度積<溶解度積 | 生成しない |
仮の溶解度積が(問題文で与えられている)溶解度積を超えている場合のみ沈殿が生成する。
今回の問題文中にあるAgClの溶解度積は1.8×10ー10(mol/L)2で、求めた仮の溶解度積が2.0×10ー10(mol/L)2なので…
\[ \underbrace{ 2.0×10^{-10} }_{ 仮の溶解度積 } > \underbrace{ 1.8×10^{-10} }_{ 真の溶解度積 } \]
仮の溶解度積>真の溶解度積となり沈殿は生成する。
演習問題
化学のグルメでは、高校化学・化学基礎の一問一答問題を公開しています。問題一覧は【スマホで出来る】一問一答(高校化学・化学基礎)でご覧下さい。
飽和溶液において、沈殿の一部が溶解し平衡状態になることを【1】という。
解答/解説:タップで表示
解答:【1】溶解平衡
飽和溶液において、沈殿の一部が溶解し平衡状態になることを溶解平衡という。

塩化銀AgClを水に溶解させると、一部のAgClが溶け残った水溶液ができ、溶解平衡の状態に達した。この溶解平衡の平衡定数K(AgCl)は次のように表される。
\(K(\mathrm{AgCl}) = \frac{[【1】][【2】]}{ [\mathrm{AgCl}(固)]}\)
[AgCl(固)]を一定とみなし、新しい定数としてKs(AgCl)を次のように定義する。
\(K_{\mathrm{s}}(\mathrm{\mathrm{AgCl}}) =[【1】][【2】]\)
このKs(AgCl)を(塩化銀の)【3】という。
解答/解説:タップで表示
解答:【1】Ag+【2】Clー【3】溶解度積(【1】・【2】は順不同)
塩化銀AgClの溶解度を求めよ。ただし、AgClの溶解度積は4.0×10-10(mol/L)2とする。
解答/解説:タップで表示
解答:2.0×10ー5(mol/L)
溶けるAgClをx(mol/L)とすると、Ag+、Cl–の濃度はどちらもx(mol/L)となる。
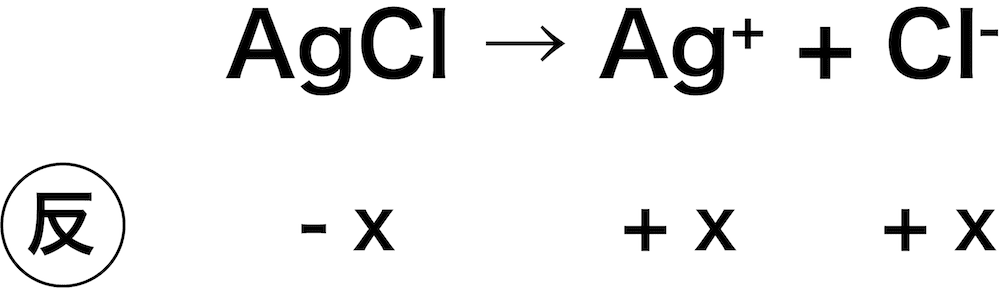
したがって、次のような式を立てることができる。
\[ \begin{align}&K_{\mathrm{sp}}(\mathrm{AgCl}) = \mathrm{[Ag^{+}][Cl^{-}]}\\
&\leftrightarrow 4.0×10^{-10} = x × x\\
&\therefore x = 2.0×10^{-5}(\mathrm{mol/L})\end{align} \]














