MENU
化学反応式(係数・作り方・書き方・計算問題の解き方など)
はじめに
【プロ講師解説】このページでは『化学反応式(係数・作り方・書き方・計算問題の解き方など)』について解説しています。
原子・分子とは
- 化学反応式について説明する前に、原子・分子について少し復習する。
原子=小さなツブ
- 物質の最小構成単位で小さくて丸いツブを原子という。

- この図は左から、水素原子・酸素原子・塩素原子を表している。すべての物質はこのような丸いツブからできている。
参考:【原子の構造】陽子・中性子・電子・原子核・質量数・原子番号の数と関係
分子=いくつかの原子がくっついたもの
- 複数の原子が結合してできた粒子を分子という。
- 例えば、水素”分子”は2つの水素”原子”が繋がることによって形成されている。
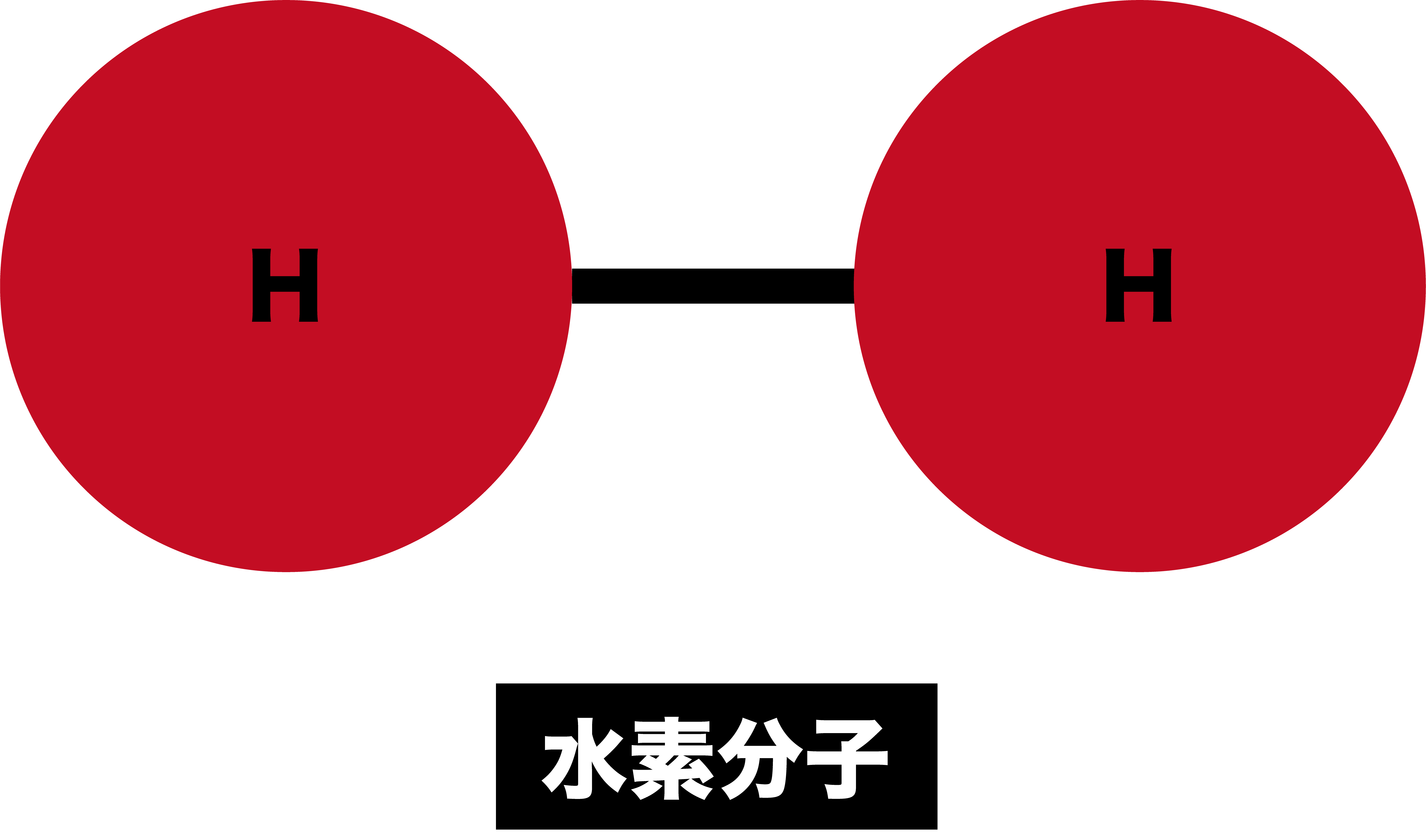
化学反応とは
化学反応=結合ペアの変化
- 分子内の結合が切れて新たな結合ができ、別の物質に変わることを化学反応という。

- この例では、水素同士、塩素同士の結合が切れて、水素と塩素で新たに結合をつくっている。つまり「結合のペア」が変化したわけである。
- ここで1つ、とても重要なルールを紹介する。
化学反応の前後で、原子の数は変わらない
- 化学反応が起こるとき、反応の前後で原子の数は変わらない。

- 先ほど挙げた例でも、左側と右側の水素原子・塩素原子の数はそれぞれ等しくなっている。
これは化学反応式をつくっていくときに知っておかなければいけない大切なルールなので、必ず覚えておきましょう。
化学反応式とは
- 化学反応を化学式を用いて表した式を化学反応式という。
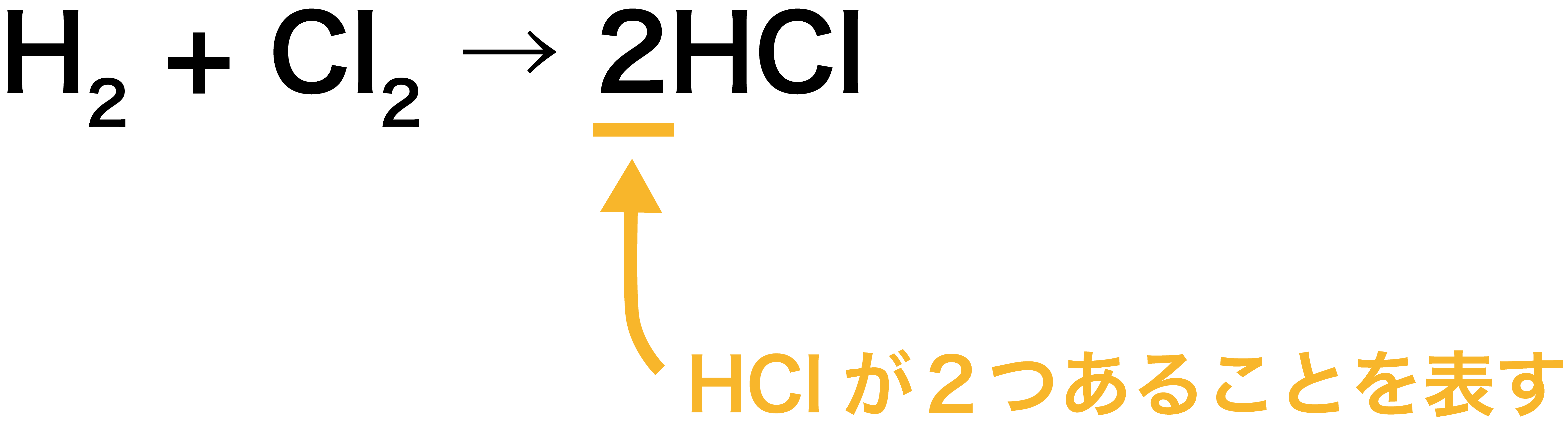
- 例えば、水素と塩素の反応だと次のようになる。
\[ \mathrm{H_{2} + Cl_{2} → 2HCl} \]
- これは、先ほどの図(↓)を水素分子・塩素分子・塩化水素それぞれの分子式(化学式)、H2・Cl2・HClを使って表現したものとなっている。

- また、左に水素H原子が2個、塩素Cl原子が2個あるため、HClが「2個」できていることにも注目しよう。分子が2個あるというのを表すためには、分子の前に係数「2」を付ける。
化学反応式の係数決定
- 先ほど書いた「化学反応のルール」をもう一度確認する。
化学反応の前後で、原子の数は変わらない
- これから先はこのルールを念頭におき、みていこう。それでは、具体的な例を用いて解説する。
エタンC2H6の燃焼反応を表す化学反応式を書け。
- 係数決定は、次のステップにしたがって進める。
●STEP1
最も複雑な物質の係数を1とする。
●STEP2
両辺で各原子の数が等しくなるように調節する。
まずは、最も複雑な物質の係数を1とする。
\[ \mathrm{\textcolor{red}{1}C_{2}H_{6} + O_{2} → CO_{2} + H_{2}O} \]
※係数が1の場合は通常省略するが、わかりやすくするためにここでは書く。
①
C原子の数が左右で等しくなるようCO2の係数を2とする。
\[ \mathrm{\textcolor{red}{1}C_{2}H_{6} + O_{2} → \textcolor{red}{2}CO_{2} + H_{2}O} \]
②
H原子の数が左右で等しくなるようH2Oの係数を3とする。
\[ \mathrm{\textcolor{red}{1}C_{2}H_{6} + O_{2} → \textcolor{red}{2}CO_{2} + \textcolor{red}{3}H_{2}O} \]
③
O原子の数が左右で等しくなるようO2の係数を7/2とする。
\[ \mathrm{\textcolor{red}{1}C_{2}H_{6} + \frac{ 7 }{ 2 }O_{2} → \textcolor{red}{2}CO_{2} + \textcolor{red}{3}H_{2}O} \]
④
化学反応式の係数が分数だとマズイので全体に2をかける。
\[ \mathrm{\textcolor{red}{2}C_{2}H_{6} + \textcolor{red}{7}O_{2} → \textcolor{red}{4}CO_{2} + \textcolor{red}{6}H_{2}O} \]
特殊な方法「未定係数法」
- 複雑な反応式の係数を求めるときには未定係数法という特殊な方法を用いることが多い。
- 未定係数法について詳しくは次のページを参照のこと。
化学反応式と単位計算
- ここからは、化学反応式を使った計算問題の解き方について解説する。
- まずはじめに、化学反応式について1つ押さえておくべきことがある。
係数比=モル比
- 化学反応式における係数の比はモル比を表している。
- 例として、次の化学反応式をみてみよう。
\[ \mathrm{N_{2} + 3H_{2} → 2NH_{3}} \]
- 反応式中の係数に注目する。窒素分子(N2)・水素分子(H2)・アンモニア(NH3)の係数はそれぞれ、1・3・2となっている。
- この場合、係数から1molのN2と3molのH2が反応して2molのNH3ができるということがわかる。
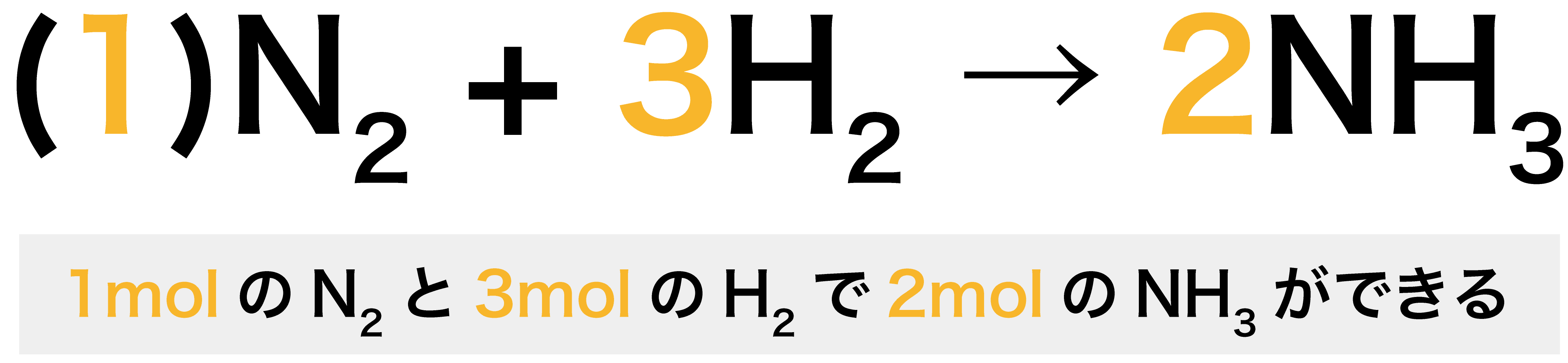
- また「係数比=mol比」と考えて単位計算をすることで、自分がそのとき必要な単位を求めることもできる。

この表が意味がよくわからない…という人は【モル計算】単位を駆使!物質量molが絡む問題の解法(原子量・体積・アボガドロ数など)を確認しましょう。
化学反応式を使った反応量計算
- 化学反応は「過不足(何かの物質が多かったり、逆に少なかったり)が生じない反応」と「過不足が生じる反応」に分けることができる。
過不足が生じない問題
プロパンC3H8の燃焼反応(C3H8 + 5O2→ 3CO2 + 4H2O)について、次の問いに答えよ。
(1)2.0molのC3H8が燃焼すると、何molのCO2が生成するか。
(2)3.0×1023個のC3H8が燃焼すると、何molのH2Oが生成するか。
(3)3.0molのC3H8が燃焼すると、何gのH2Oが生成するか。
(4)2.0molのC3H8が燃焼すると、何LのCO2が生成するか。
(5)3.0×1023個のC3H8が燃焼すると、何LのCO2が生成するか。
- この問題を解く上で、次の表をテンプレートとして用いる。
- (基)は基本となる物質の量を、(今)は今回の問題に書かれている量を示す。
(1)
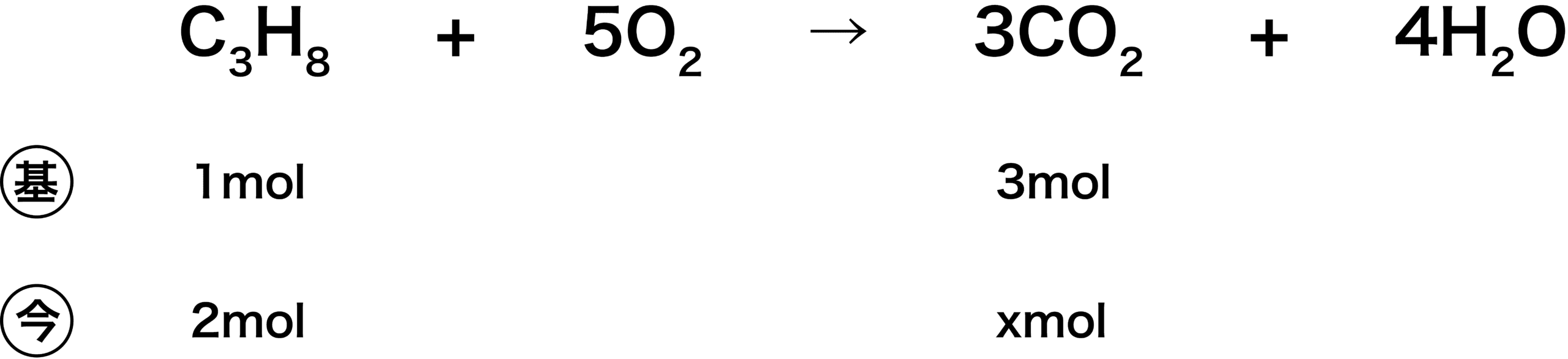
- (基)のところには、(「係数比=モル比」であることを考慮すると、1molのC3H8から3molのCO2ができるとわかるので、)C3H8の下に1mol、CO2の下に3molと書き込む。
- 次に、今回は2molのC3H8が反応しているので、(今)のところにそれを書き込む。また、CO2が何mol出てくるかを求めたいため、そこはxとおいておく。
- あとは、比を利用することで簡単に答えを求めることができる。
\[ \begin{align}
&\mathrm{1:3 = 2:x}\\
&\mathrm{↔ x=6}
\end{align} \]
- よって、答えは6.0molである。
(2)
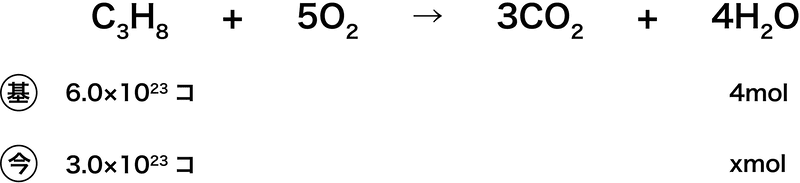
- (基)の所に書いてある6.0×1023個とは、アボガドロ定数に(C3H8の係数が1のため)1molをかけたものである。
\[ \mathrm{6.0×10^{23}(個/mol) × 1(mol) = 6.0×10^{23}(個)} \]
- 縦の列で(つまり同じ物質で)単位が揃っていれば、横で単位が違っても(1)と同じように比を使って解くことができる。
\[ \begin{align}
&\mathrm{6.0×10^{23}:4 = 3.0×10^{23}:x}\\
&\mathrm{↔ x=2}
\end{align}\]
- よって、答えは2.0molである。
(3)
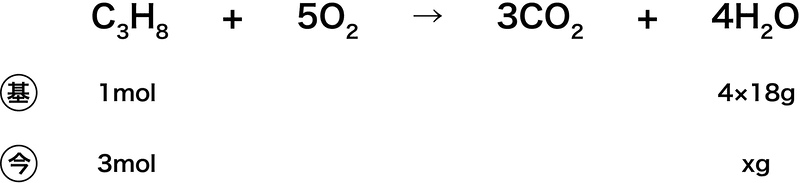
- 4×18gというのは、H2Oの物質量である18g/molに(H2Oの係数が4のため)4molをかけたものである。したがって、次のような式をつくることができる。
\[ \mathrm{4(mol)×18(g/mol)=4×18(g)} \]
- 後は比を用いて解く。
\[ \begin{align}&\mathrm{1:4×18 = 3:x}\\
&\mathrm{↔ x=216}\end{align} \]
- よって、答えは216gである。
(4)
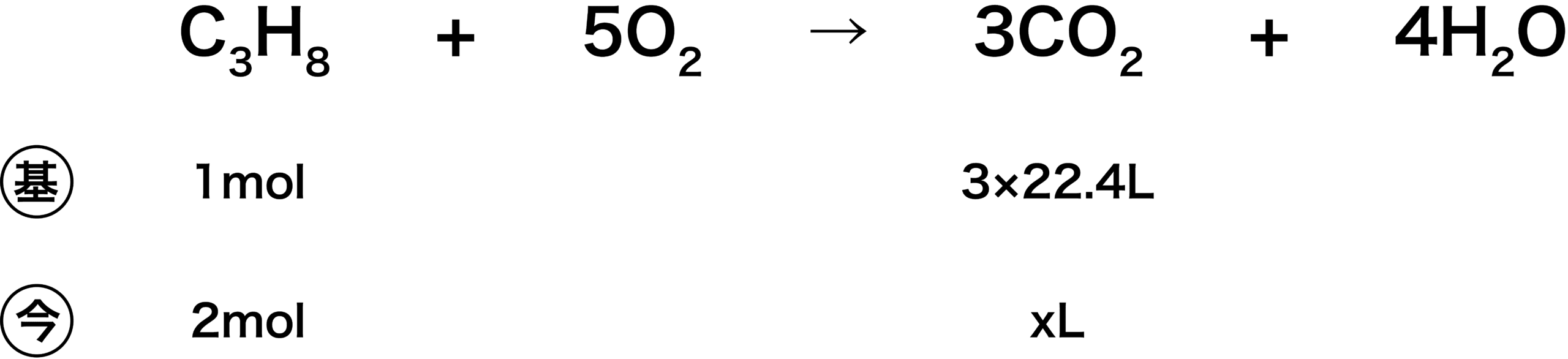
- 3×22.4[L]というのは、標準状態での気体の1molあたりの体積である22.4[L/mol]に(CO2の係数が3のため)3molをかけたものである。したがって、次のような式をつくることができる。
\[ \mathrm{3(mol)×22.4(L/mol)= 3×22.4(L)} \]
- 後は比を用いて解く。
\[ \begin{align}&\mathrm{1:3×22.4 = 2:x}\\
&\mathrm{↔ x=134.4(L)}\end{align} \]
- よって、答えは134.4Lである。
(5)
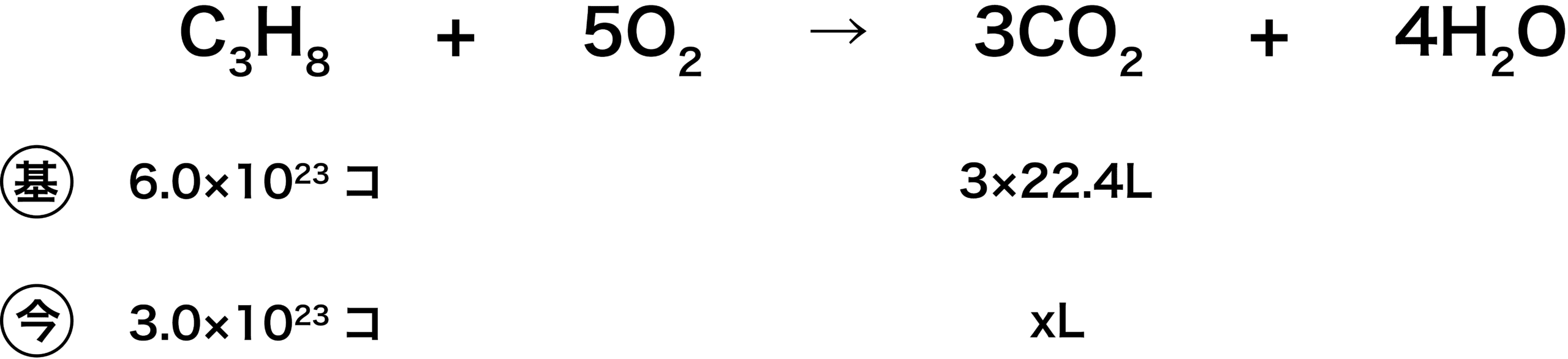
- 6.0×1023個というのは、アボガドロ定数に(C3H8の係数が1のため)1molをかけたものである。
\[ \mathrm{6.0×10^{23}(個/mol) × 1(mol) = 6.0×10^{23}(個)} \]
- 3×22.4Lというのは、標準状態での気体の1molあたりの体積である22.4L/molに(CO2の係数が3のため)3molをかけたものである。
\[ \mathrm{3(mol)×22.4(L/mol)= 3×22.4(L)} \]
- 後は比を用いて解く。
\[ \begin{align}&\mathrm{6.0×10^{23}:3×22.4 = 3.0×10^{23}:x}\\
&\mathrm{↔ x=33.6}\end{align} \]
- よって、答えは33.6Lである。
過不足が生じる問題
窒素N2と水素H2の反応(N2 + 3H2 → 2NH3)について、1molのN2と4molのH2を反応させたとき、生じるアンモニアNH3は何molか。また、何が何mol余るか。
- 過不足ありの場合はこのテンプレートを使う。
- (前)は反応前の量、(反)は反応した量、(後)は反応後の量を表している。
- 今回は、1molのN2と、4molのH2を反応させたため、それを(前)のところに書き込む。また、反応前のためNH3はまだ0molである。
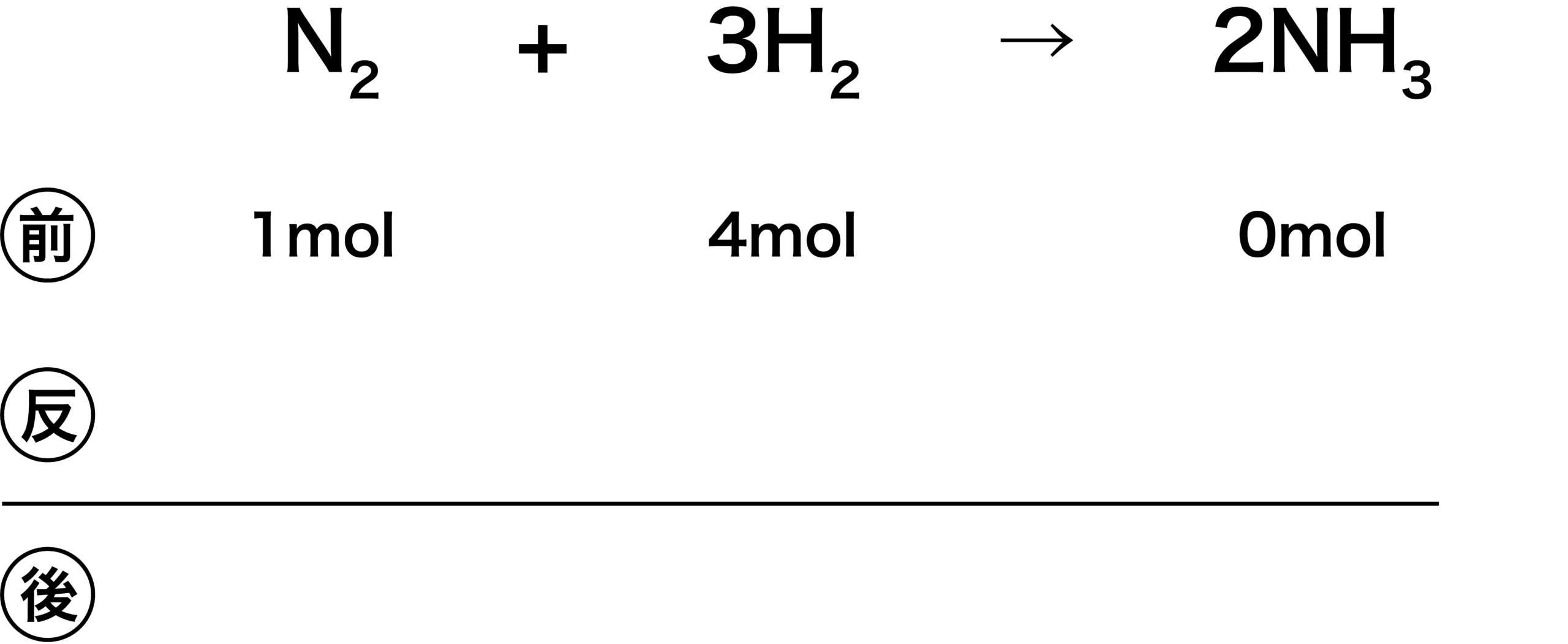
- ここでポイントとなるのが「余る物質を予想すること」である。この予想はハズレても後でわかるので問題ない(予想が外れたときの例と判別法は後に記載)。余る物質を予想したら、余らないと思う物質が反応後「0」になるように引き算をする。
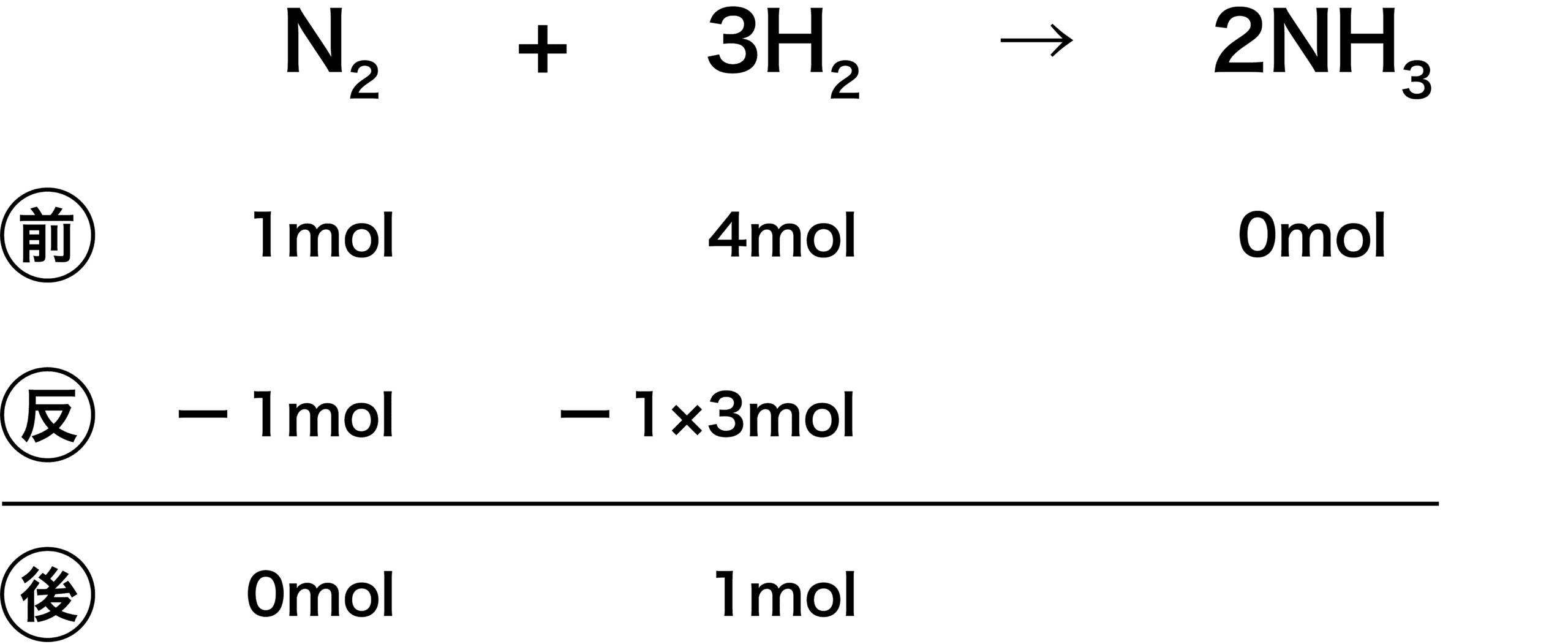
- 今回の例では、化学反応式より、N2とH2は1:3で反応する。したがって、今N2が1[mol]、H2が4[mol]あるため、余るのはH2だと考えられる。つまり、余らないのはN2であり、N2が反応後「0」になるように引き算する。
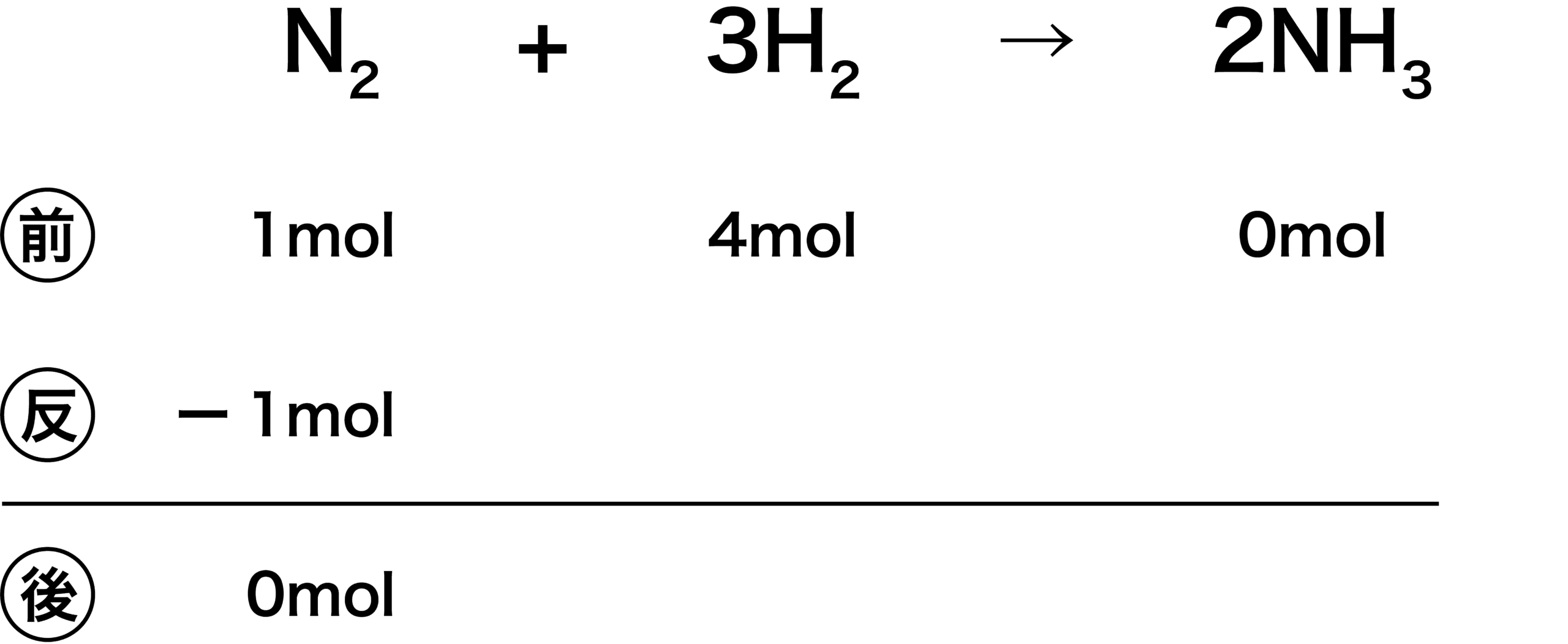
- 次に、N2とH2の係数に注目する。N2が1mol反応するときH2はその3倍の3mol反応する。
\[ \mathrm{N_{2}:H_{2}=1:3} \]
- よって、下図のようになる。
- 次に、N2とNH3の係数に注目する。N2が1mol反応するとき、NH3はその2倍の2mol生成する。
\[ \mathrm{N_{2}:H_{2}=1:3} \]
- よって、次のようになる。
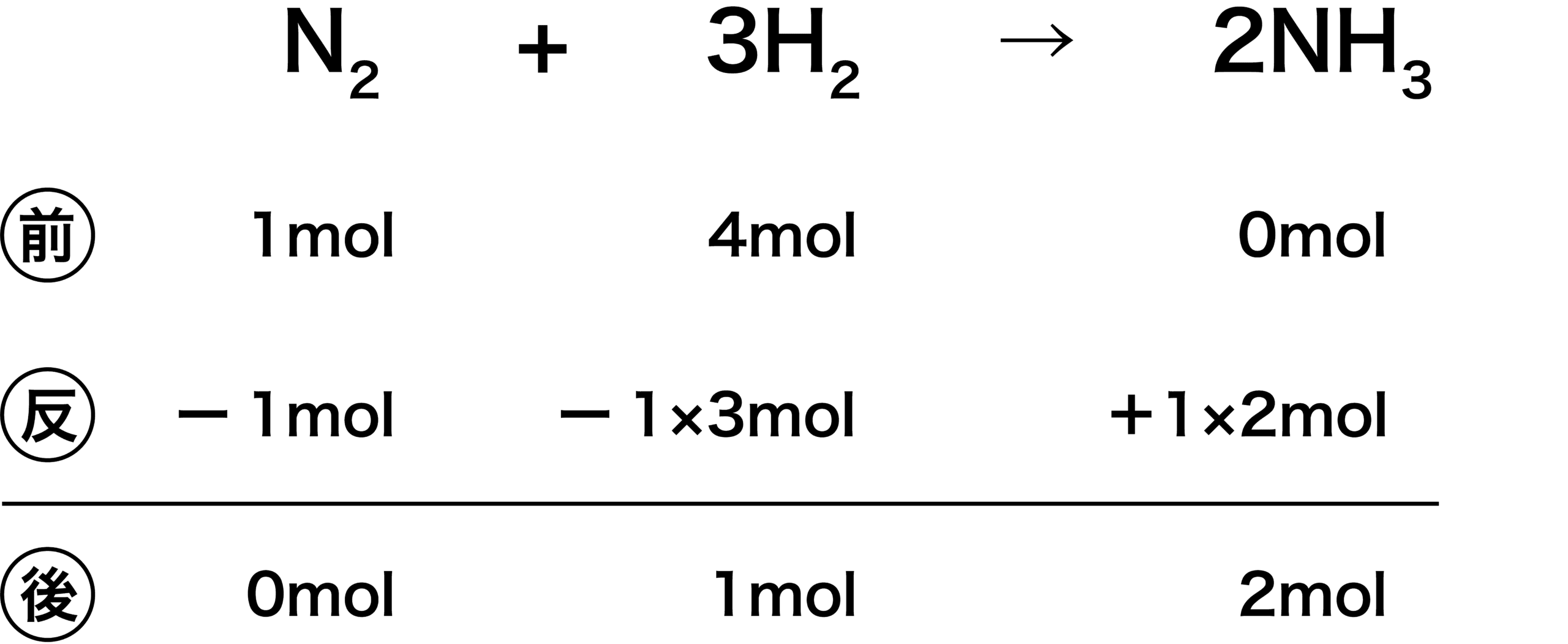
- この表から、「NH3が2molできて、1molのH2が余る」ことがわかる。
余る物質の予想が外れたとき
- 余る物質の予想が外れたとき、それを判断する方法を解説する。
- 先ほどと同じ反応で、N2が余ると予想する。すると、余らない物質はH2ということになるため、H2が反応後「0」になるように引く。
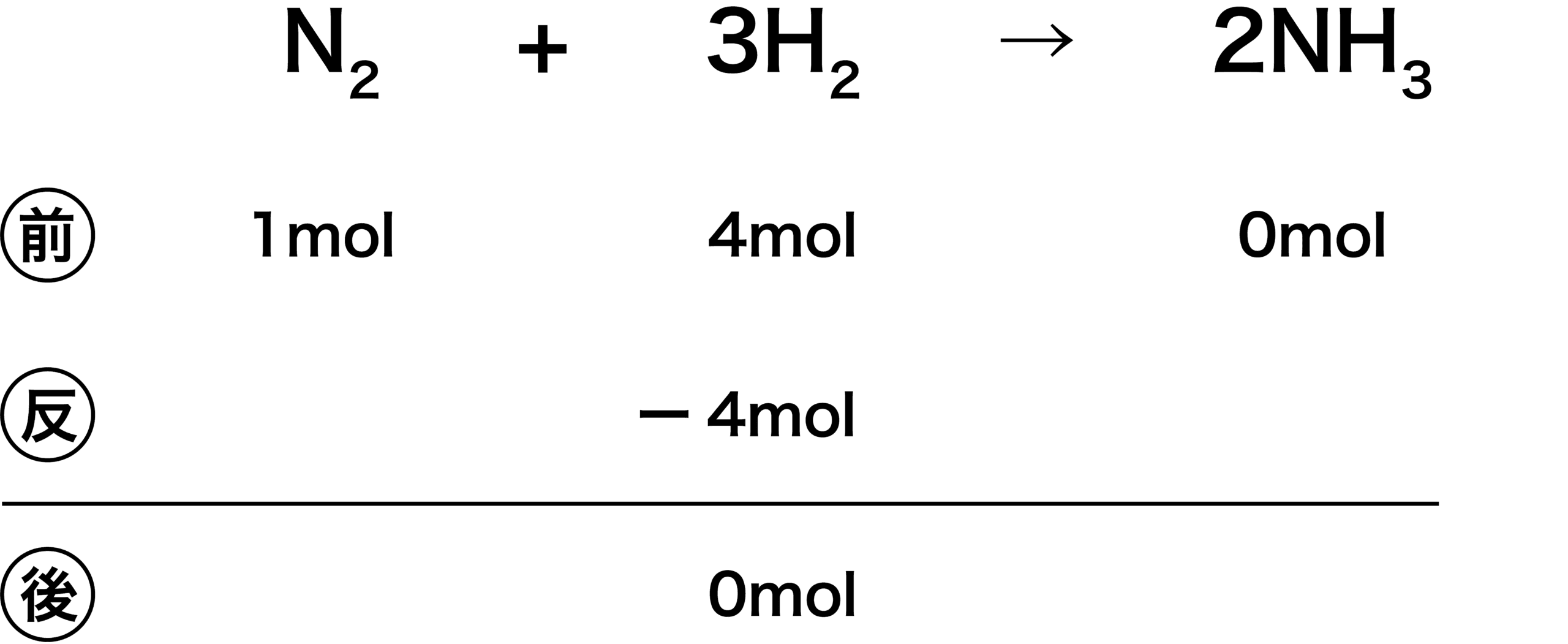
- 次に、N2について考える。係数比からN2:H2=1:3で反応するため、 N2はH2の1/3倍の「4×1/3mol」反応するはずである。
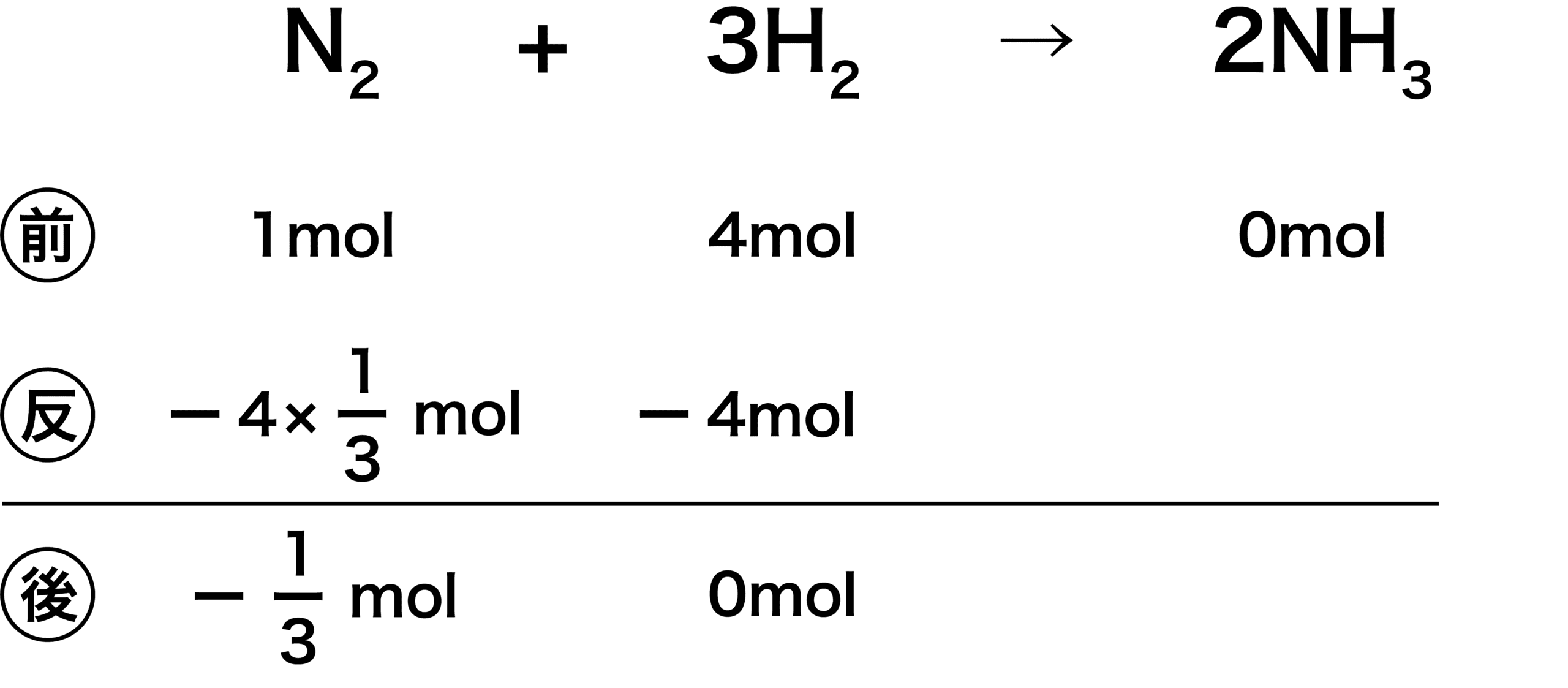
- 反応後のN2がマイナスになっている。反応後の値がマイナスになることは通常あり得ないため、ここで予想が外れていたと気づく。このような形で予想の当たり外れを知ることができる。














