MENU
圧平衡定数（公式の導出や計算問題の解き方など）
目次
はじめに
【プロ講師解説】このページでは『圧平衡定数（公式の導出や計算問題の解き方など）』について解説しています。
圧平衡定数
- 気相での化学平衡は、気体の濃度で表した平衡定数以外に、気体の分圧で表した平衡定数を用いることがある。
\[ \mathrm{2CO(気)+O_{2}(気)⇄2CO_{2}(気)} \]
- 【化学平衡】平衡定数やmol数の変化、グラフなどにあるように、この反応の平衡定数Kを表すと次のようになる。
\[ K=\frac{ [\mathrm{CO_{2}}]^{2} }{ [\mathrm{CO}]^{2}[\mathrm{O}_{2}] }・・・① \]
- 気体の濃度(mol/L)は、単位体積あたりの物質量(mol)で表されるので、次のようになる。
\[ \begin{align}&[\mathrm{CO}]=\frac{ n_{\mathrm{O}} }{ V }\\
&[\mathrm{O_{2}}]=\frac{ n_{\mathrm{O_{2}}} }{ V }\\
&[\mathrm{CO_{2}}]=\frac{ n_{\mathrm{CO_{2}}} }{ V }\end{align} \]
- ここで、これらの気体を理想気体とみなし、気体の状態方程式PV=nRTを適応すると…
\[ [\mathrm{CO}]=\frac{ n_{\mathrm{CO}} }{ V }=\frac{ P_{\mathrm{CO}} }{ RT } \]
- このようになり、各気体のモル濃度は分圧を用いて表すことができるということがわかる。これを①式へ適応すると、次のようになる。
\[ \begin{align}
K&=\frac{ (\frac{ P_{\mathrm{CO_{2}}} }{ RT })^{2} }{ (\frac{ P_{\mathrm{CO}} }{ RT })^{2}×(\frac{ P_{\mathrm{O_{2}}} }{ RT }) }\\
&=\frac{ (P_{\mathrm{CO_{2}}})^{2} }{ (P_{\mathrm{CO}})^{2}×(P_{\mathrm{O}_{2}}) }×RT
\end{align} \]
- ここで、Rは気体定数なので一定、また温度Tが一定のとき平衡定数Kは一定なので…
\[ \frac{ (P_{\mathrm{CO_{2}}})^{2} }{ (P_{\mathrm{CO}})^{2}×(P_{\mathrm{O}_{2}}) }=\underbrace{ \frac{ K }{ RT } }
_{ \text{ 一定 }} \]
- ここで、K/RTをKpとおくと..
\[ K_{p}=\frac{ (P_{\mathrm{CO}_{2}})^{2} }{ (P_{\mathrm{CO}})^{2}×(P_{\mathrm{O}_{2}}) } \]
- Kpはモル濃度の代わりに、平衡時の気体の分圧を用いた平衡定数であり、圧平衡定数とよばれる。
演習問題
化学のグルメでは、高校化学・化学基礎の一問一答問題を公開しています。問題一覧は【スマホで出来る】一問一答（高校化学・化学基礎）でご覧下さい。
問1
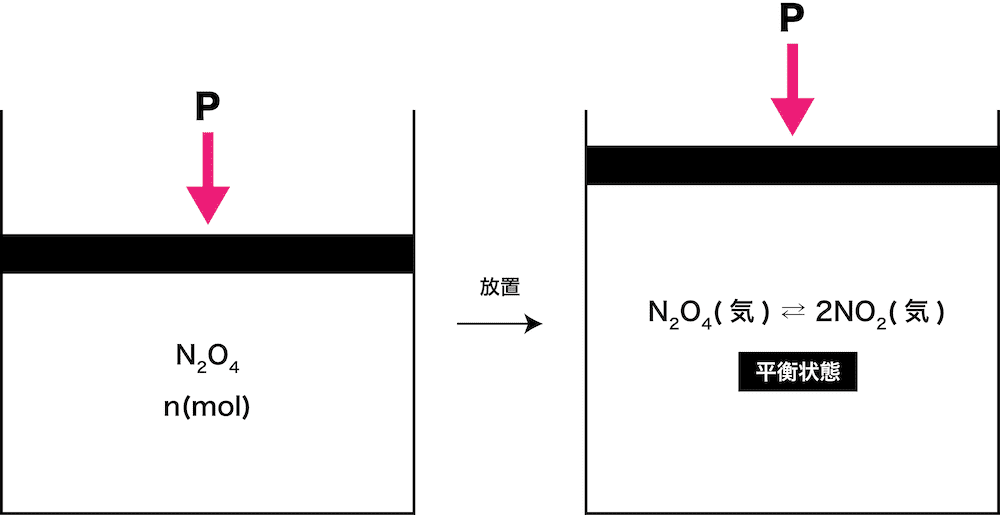
ピストンの付いた容器に四酸化二窒素N2O4n(mol)を入れ、全圧Pのもと一定温度で十分に放置すると、次の平衡状態になった。
\[ \mathrm{N_{2}O_{4}(気)⇄2NO_{2}(気)・・・①} \]
N2O4の解離度をα(0≦α≦1)とし、①式の圧平衡定数Kpを文字式で表せ。
解答/解説：タップで表示
解答：以下参照
今回求める圧平衡定数Kpは次のように表すことができる。
\[ K_{p}=\frac{ (P_{\mathrm{NO_{2}}})^{2} }{ P_{\mathrm{N_{2}O_{4}}} } \]
全圧Pが与えられているため、①式での各成分のモル分率を求め、Pにかけると分圧を求めることができる。
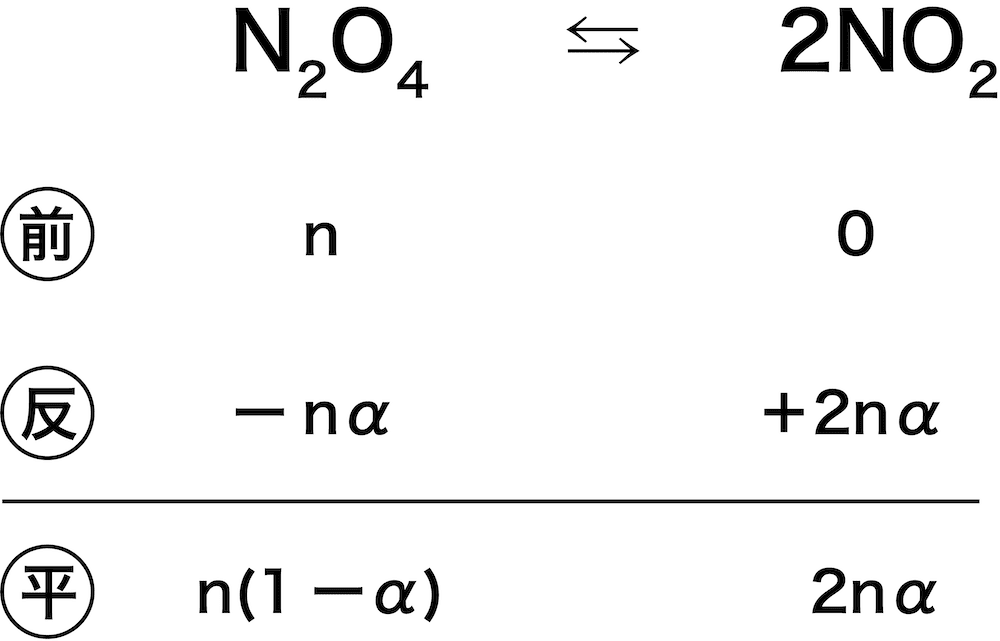
ここで、平衡時の全モル数がn(1ーα)＋2nα＝n(1＋α)molであることを考慮すると、平衡時の各気体の分圧は以下のようになる。
\[ \begin{align}
&P_{\mathrm{N_{2}O_{4}}}=P×\underbrace{ \frac{ n(1-α) }{ n(1+α) } }
_{ \mathrm{N_{2}O_{4}}のモル分率 }=P×\frac{ 1-α }{ 1+α }\\
\\
&P_{NO_{2}}=P×\underbrace{ \frac{ 2nα }{ n(1+α) } }
_{ \mathrm{NO_{2}}のモル分率 }=P×\frac{ 2α }{ 1+α }
\end{align} \]
よって、圧平衡定数Kpは…
\[ \begin{align}
K_{p}&=\frac{ (P_{\mathrm{NO_{2}}})^{2} }{ P_{\mathrm{N_{2}O_{4}}} }\\
&=\frac{ (P・\frac{ 2α }{ 1+α })^{2} }{ P・\frac{ 1-α }{ 1+α } }\\
&=P・\frac{ 4α^{2} }{ (1+α)(1-α) }\\
&=P・\frac{ 4α^{2} }{ 1-α^{2} }
\end{align} \]
【新課程対応】化学の計算ドリル大好評発売中！
高校化学・化学基礎の計算問題が苦手な人に向けた計算ドリルを発売しました。豊富な問題数で、入試頻出の計算問題の解き方を身につけることができます。
【新課程対応】無機化学ドリル発売中！
無機化学の知識を総ざらいできるオリジナル問題集ができました。解答・解説編には入試頻出事項が一通りまとめられており、まとめノート/参考書としての役割も果たします。
【新課程対応】有機化学ドリル発売中！
有機化学に関する入試頻出事項を演習することのできるオリジナル問題集が紙の本になりました。暗記項目だけではなく、計算問題や思考力が問われる問題についても触れています。
