MENU
六方最密構造(単位格子に含む原子数・配位数・高さ・充填率の求め方など)
はじめに
【プロ講師解説】このページでは『六方最密構造(単位格子に含む原子数・配位数・高さ・充填率の求め方など)』について解説しています。
六方最密構造とは
- 次のような構造を六方最密構造という。
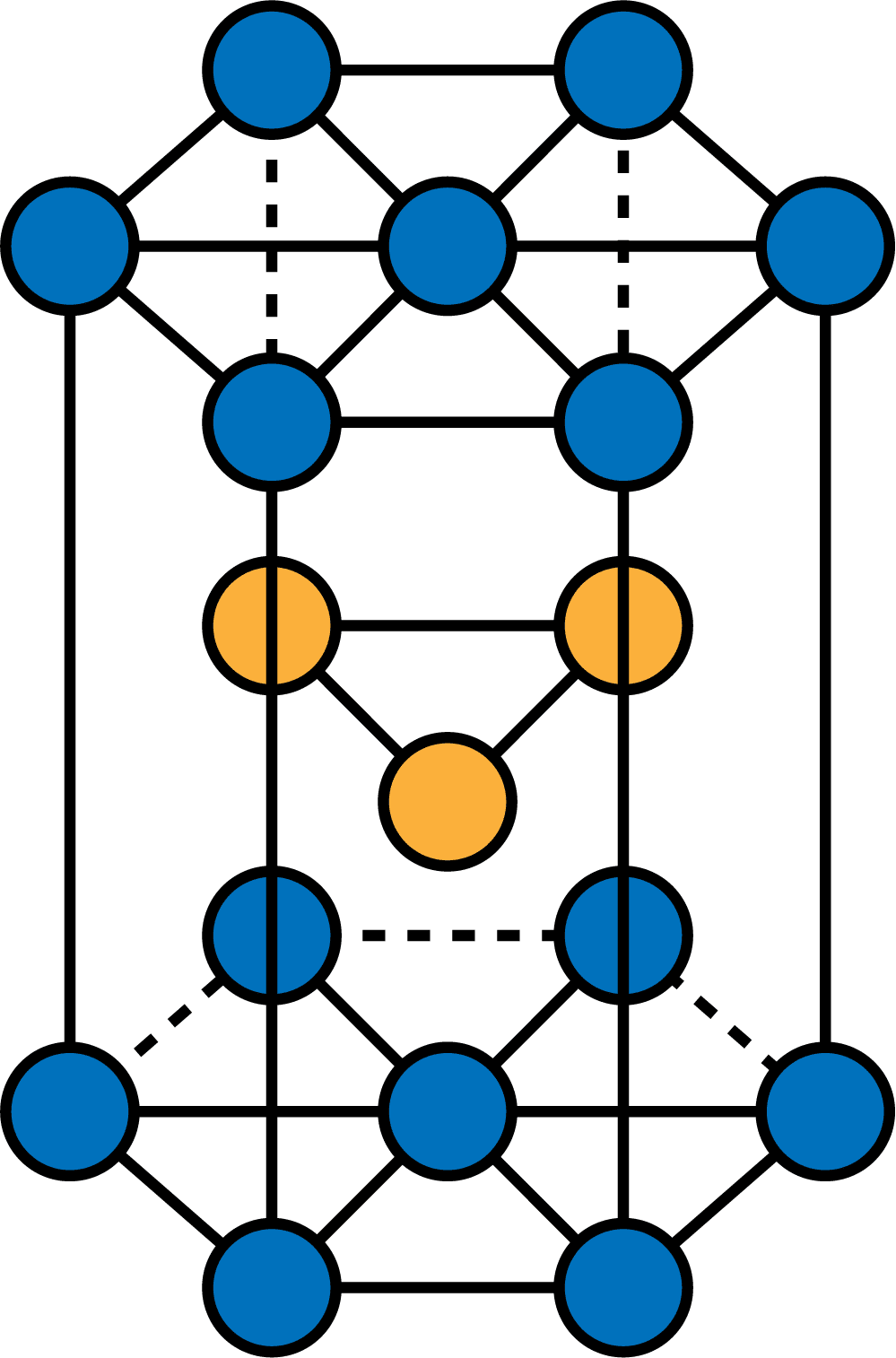
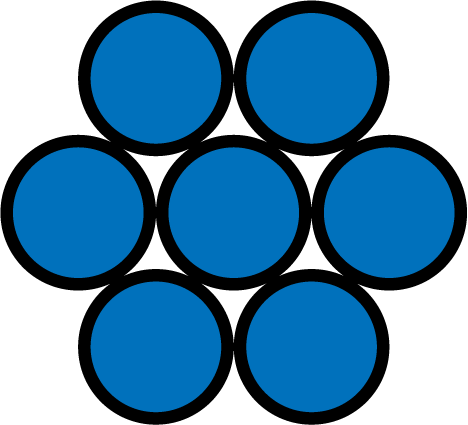
- 上下の層は、1個の原子の周りを6個の原子が取り囲む形になっている。
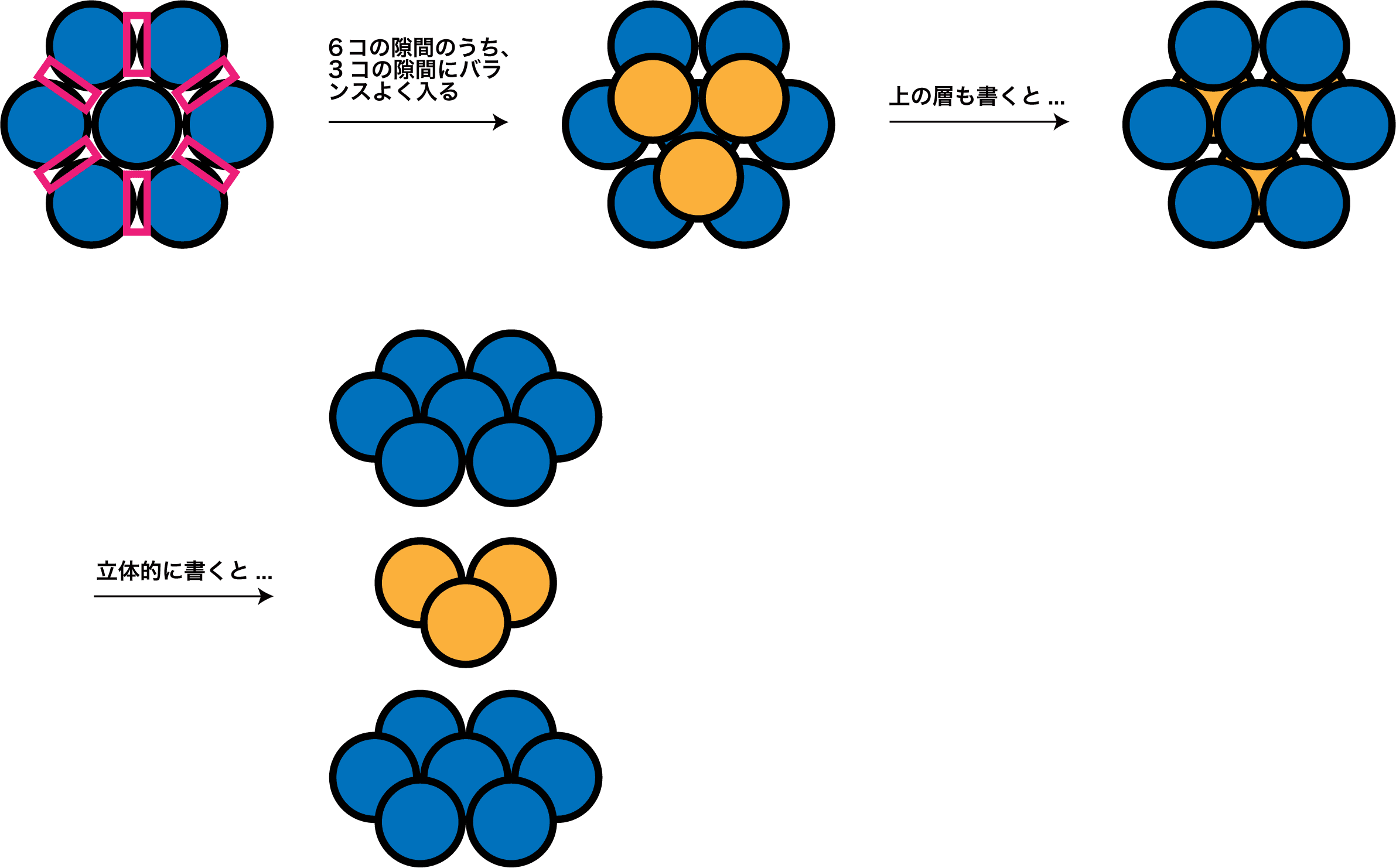
- 真ん中の層は、上下の層の「隙間」を埋めるような形で配置されている。
六方最密構造の単位格子に含まれる原子の数
- もう一度、六方最密構造の図を確認する。

- 六方最密構造はこの構造で間違いないが、六方最密構造の「単位格子(最小単位)」はこの構造の1/3である。
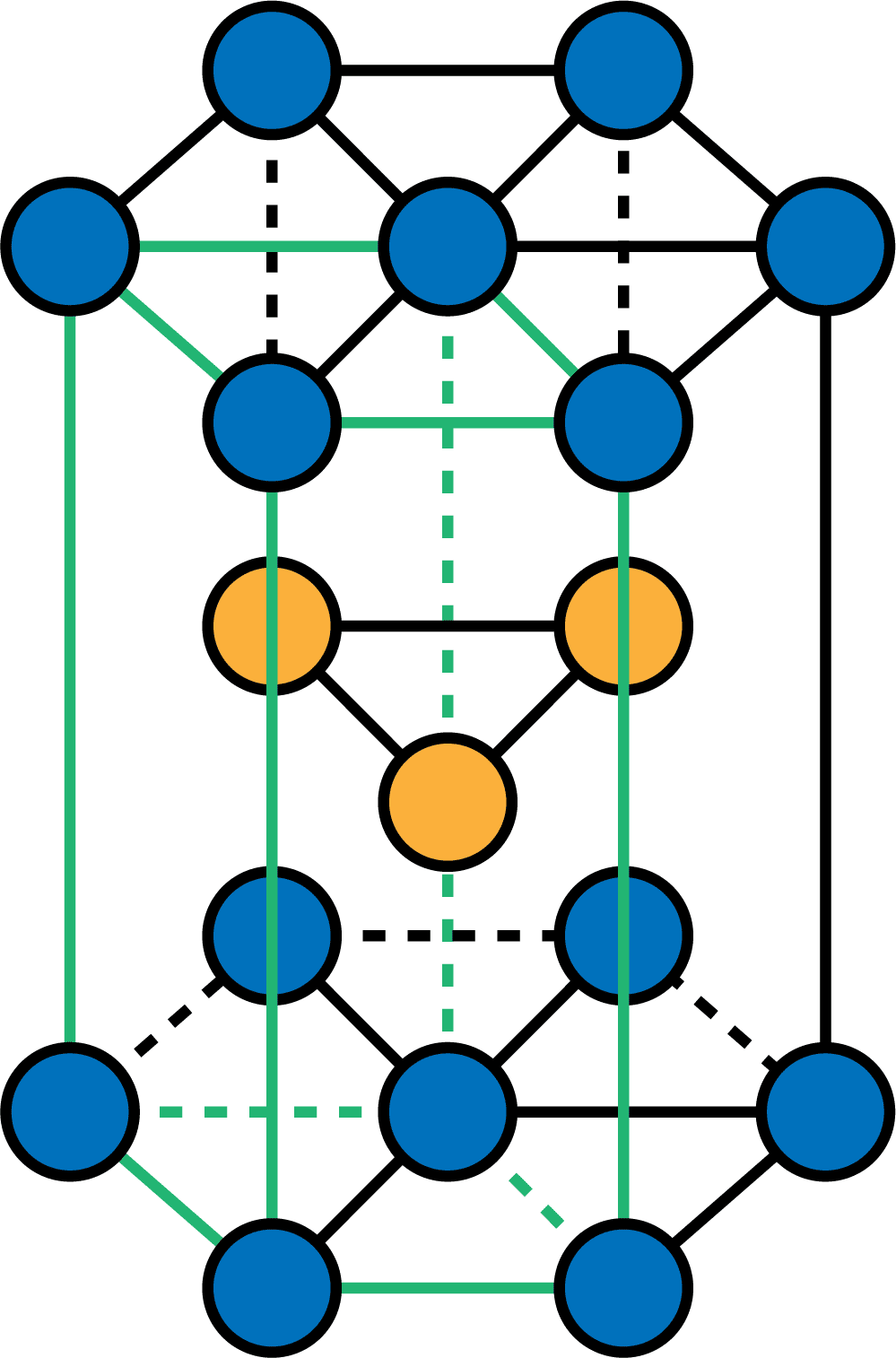
- したがって、六方最密構造の単位格子に含まれる原子の数を答えるときは、六方最密構造中の1/3に注目して考える必要がある。まず、六方最密構造を上から見た図を確認する。
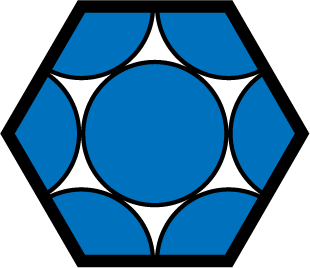
- 六方最密構造を上から見ると「正六角形」であり、したがって、1つの角度は120°である。
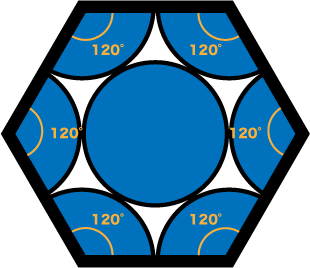
- 先ほどから述べているように、六方最密構造の単位格子は六角柱の1/3の部分のため、上からの図で考えると…
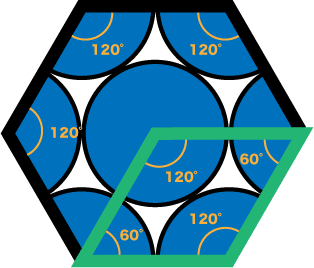
- このようになる。平行四辺形の4つの角のうち、2つの角が120°を半分にした60°になっていることに注意しよう。ここで、もう一度全体の図を見る。

- 角度が120°の割球(1/6の割球)と60°の割球(1/12の割球)は4個ずつ存在しているのがわかる。(上の面に2個ずつ、下の面に2個ずつ)
- これらの割球と、サイドに存在している「合わせて1個」の割球を考慮すると、六方最密構造の単位格子に含まれる原子の数は2個となる。
\[
\frac{ 1 }{ 12 }×4+\frac{ 1 }{ 6 }×4+1=2
\]
よくある質問
- 「合わせて1個」と書いてある部分に疑問を感じる人がいるかもしれない。
「六方最密構造では、真ん中の層に3個の原子を隙間を1つずつ空けて置いたはずなのに、なぜ隣合う2つの面に原子があるの?」なんて質問はよく受ける。 - ここについて少し詳しく説明しておこう(テストでなぜ合わせて1個なのかを問われることは考えにくい。実際には覚えておけばそれでOK)。
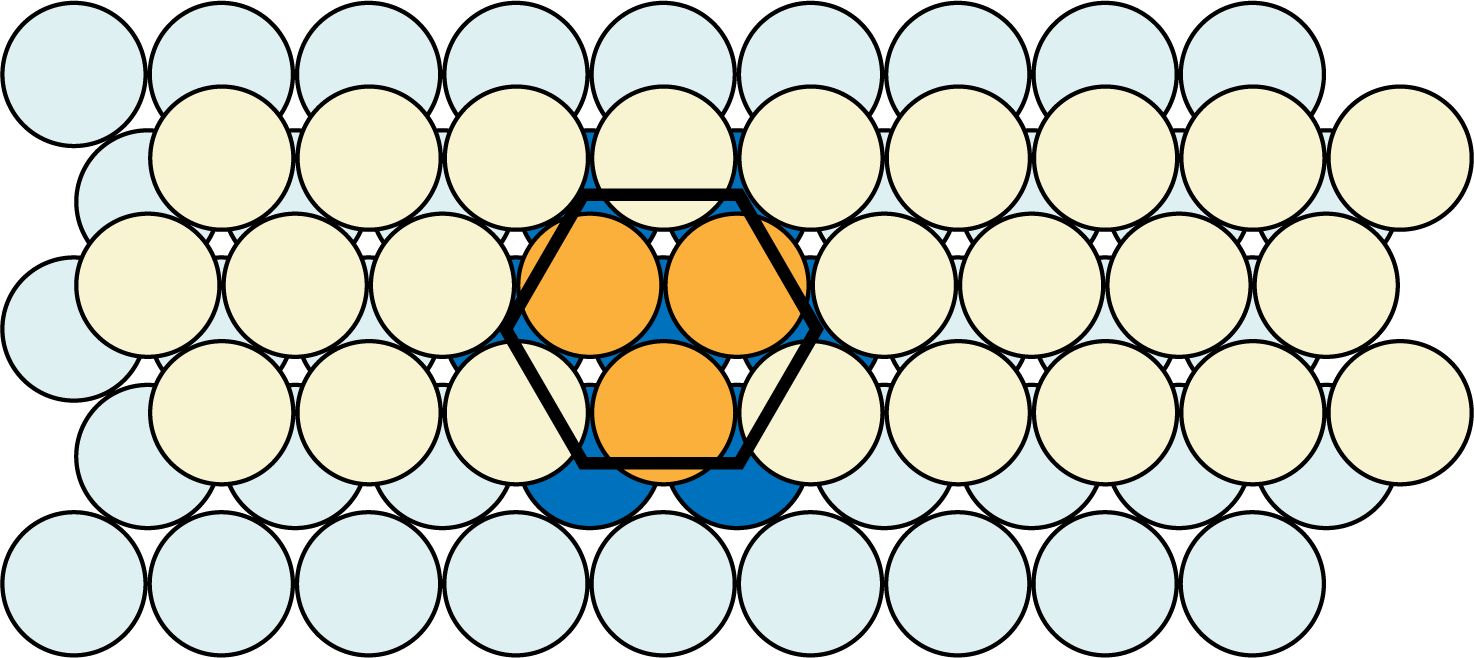
- 六方最密構造というのは、実は無数に繫がっている結晶の一部分に過ぎない。
上図の”六角形の部分(色が濃い部分)”は六方最密構造の下層と中層を表しており、本来はこれに下層と同じ配置で上層が重なりあうことで六方最密構造が完成している(上層は見やすさの関係で省いている)。 - ここで、六方最密構造の単位格子を図中に示すと、次のようになる。
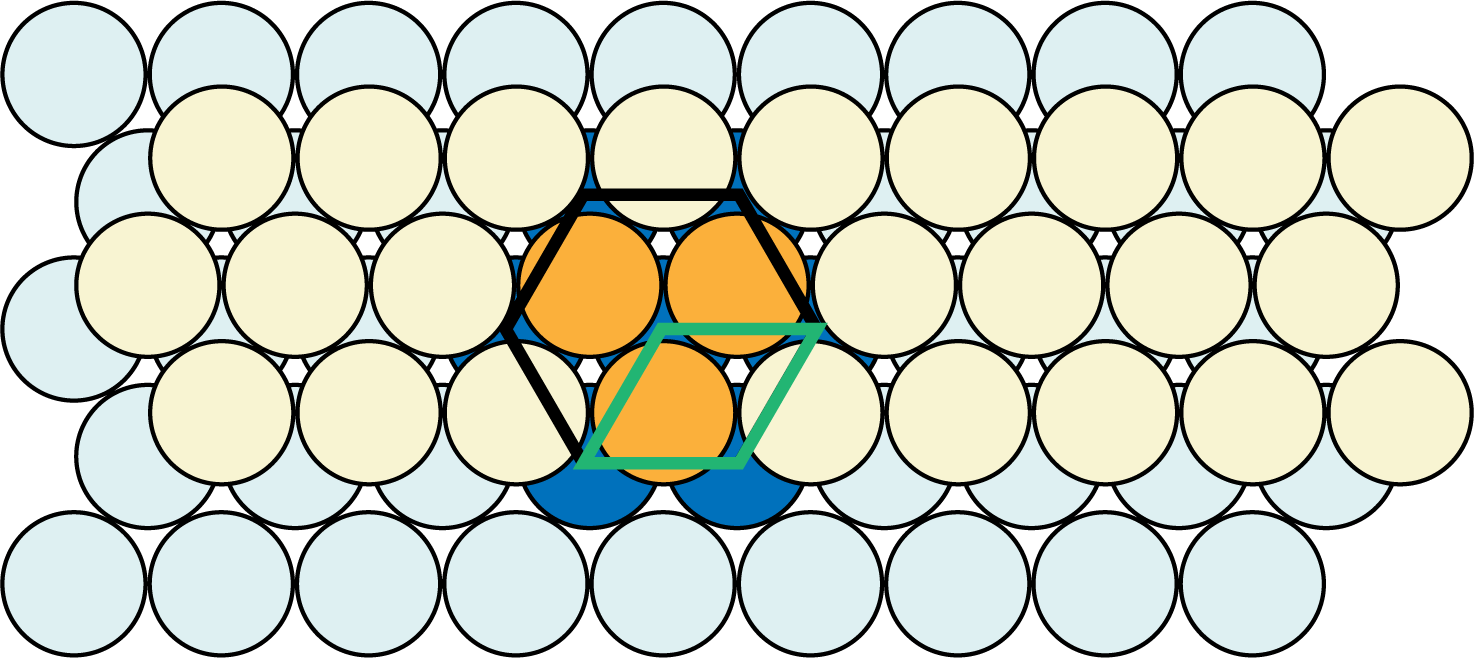
- 六方最密構造の中層の原子の一部が切り取られ、その代わり、本来中層に含まれていなかった(隣の六方最密構造の)原子の一部が取り込まれていることがわかる。
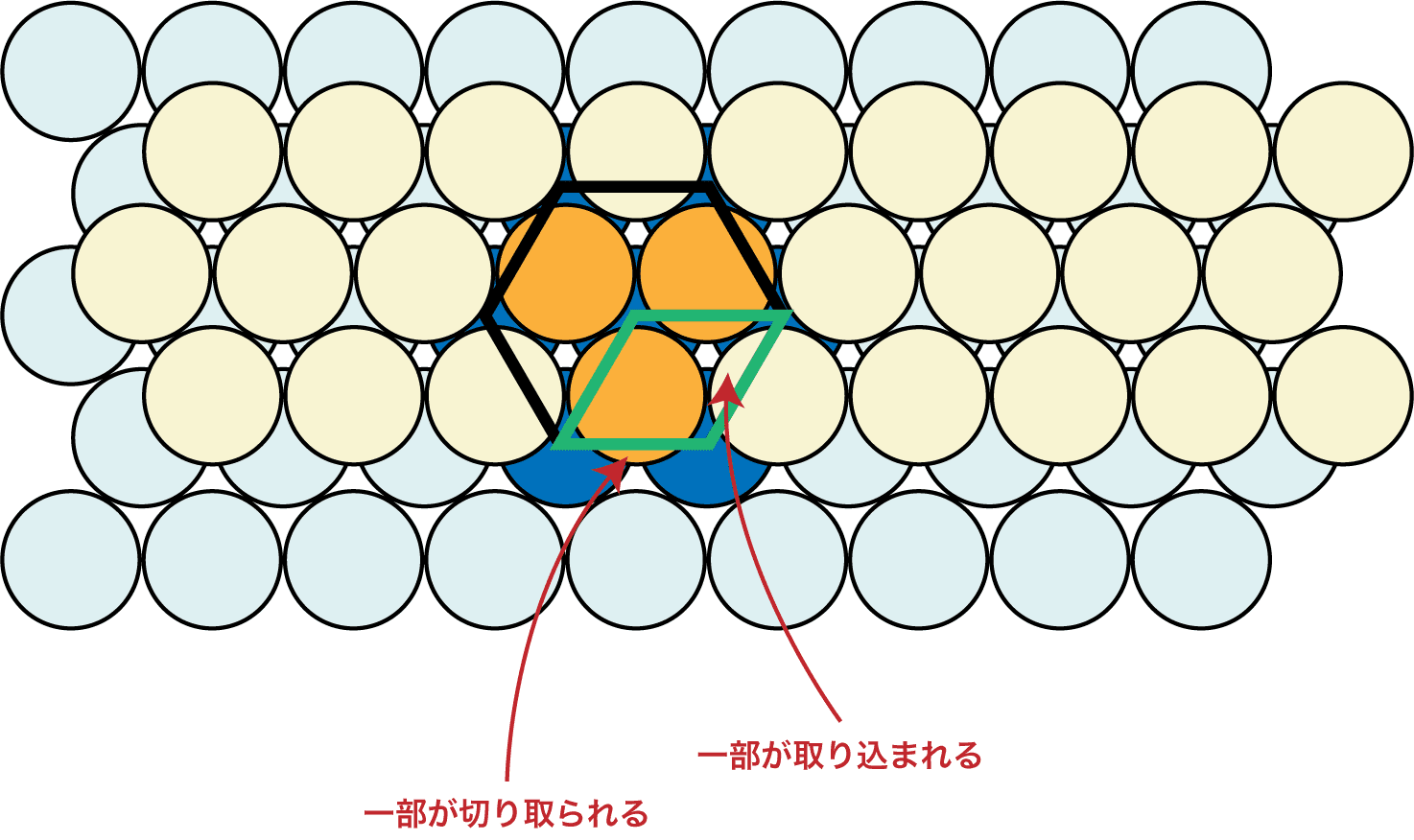
- 切り取られる部分と取り込まれる部分が一致するため、結果的に「合わせて1個」という表現がされている。
※実際に立体的な図で確認してみたいという人は次の動画(youtube)を参照
六方最密構造の配位数
- 1個の原子を取り囲む他の粒子の数を配位数という。
- 六方最密構造の中には「丸ごと1個」の状態で存在する原子がないため、2つの六方最密構造を重ねあわせて考える。
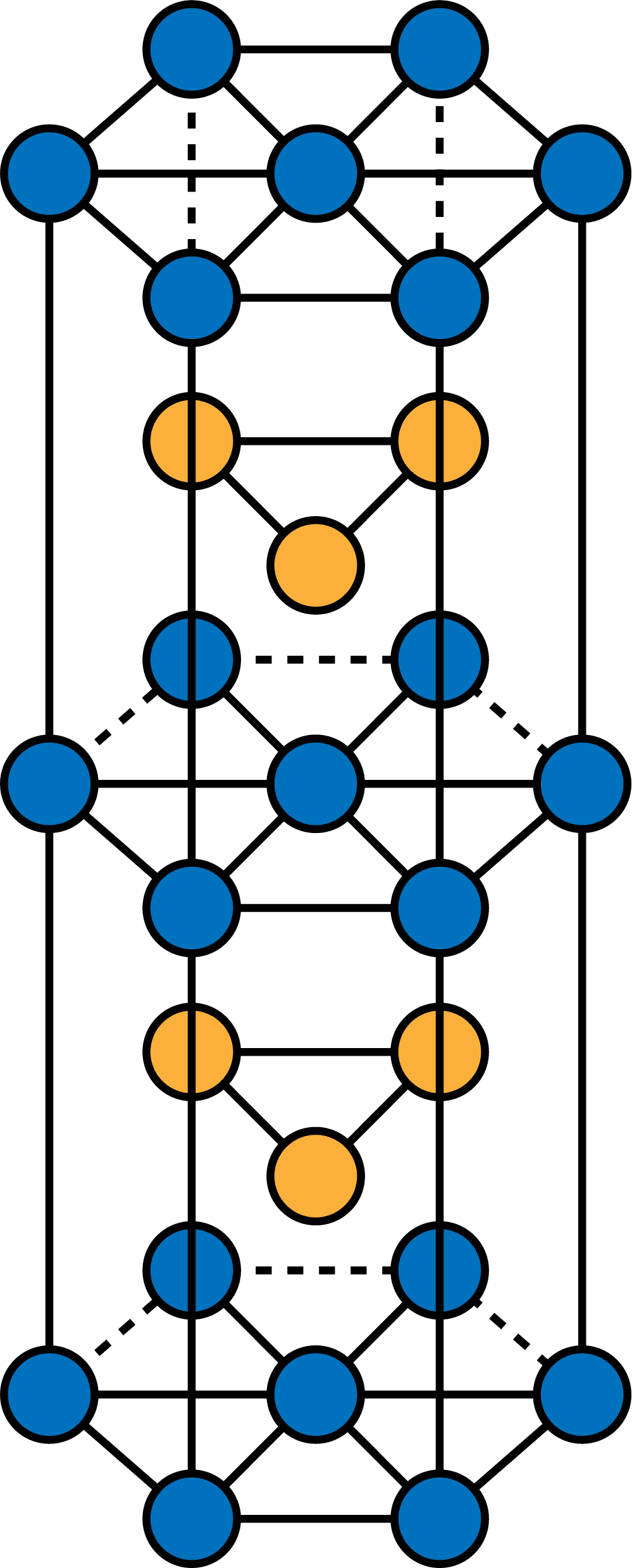
- 2つの六方最密構造を重ねあわせると、真ん中が「丸ごと1個」の原子になる。したがって、この原子に隣接する原子の数を数えれば良い。

- 六方最密構造の配位数は12である。
六方最密構造の高さの求め方と原子半径
- 六方最密構造の高さの求め方と原子半径について解説する。
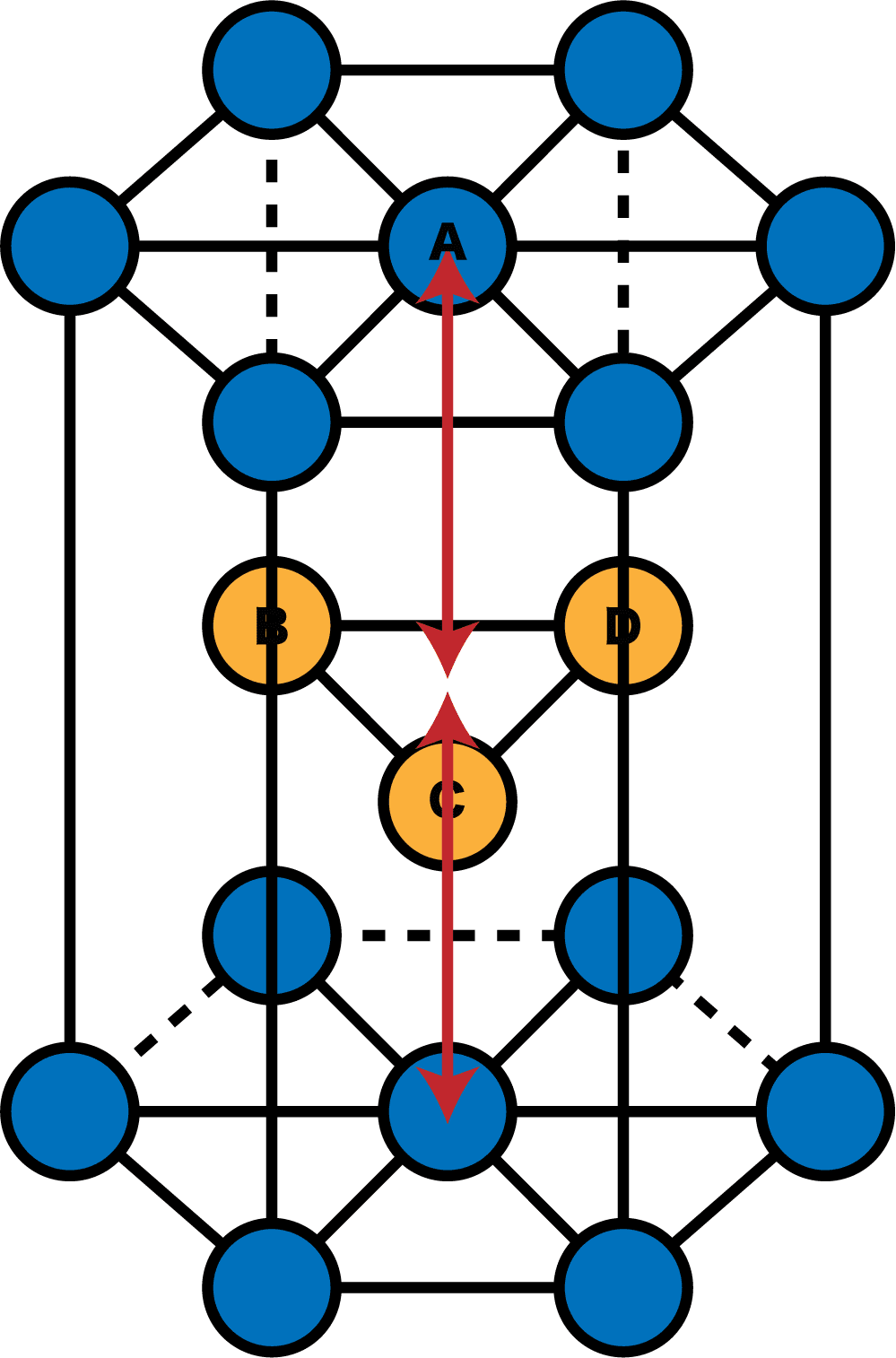
六方最密構造の高さとして、次の赤矢印の部分を測定する。
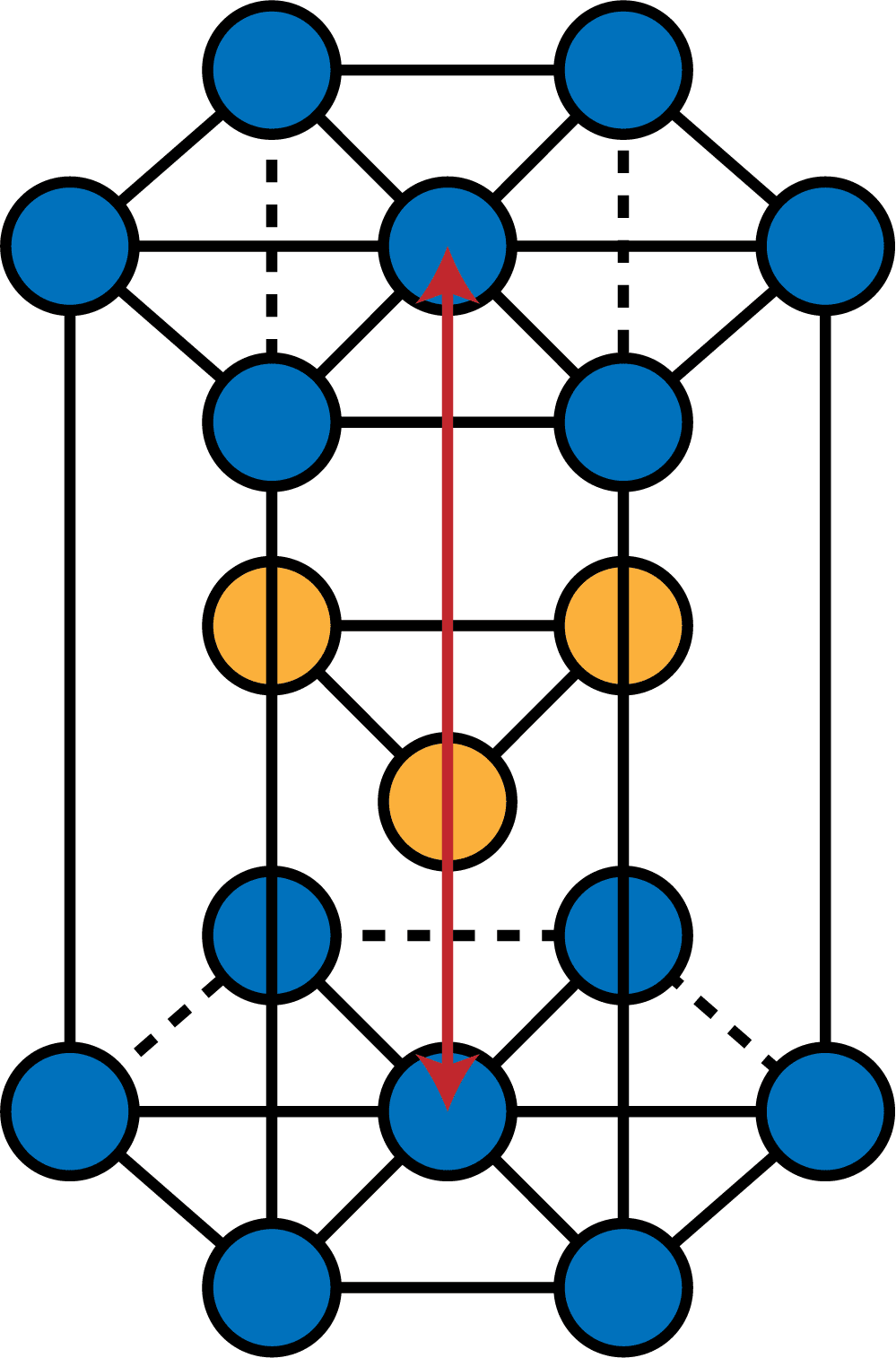
この長さを一気に測るのは大変なので「半分の長さを測って2倍する」という方針でいく。
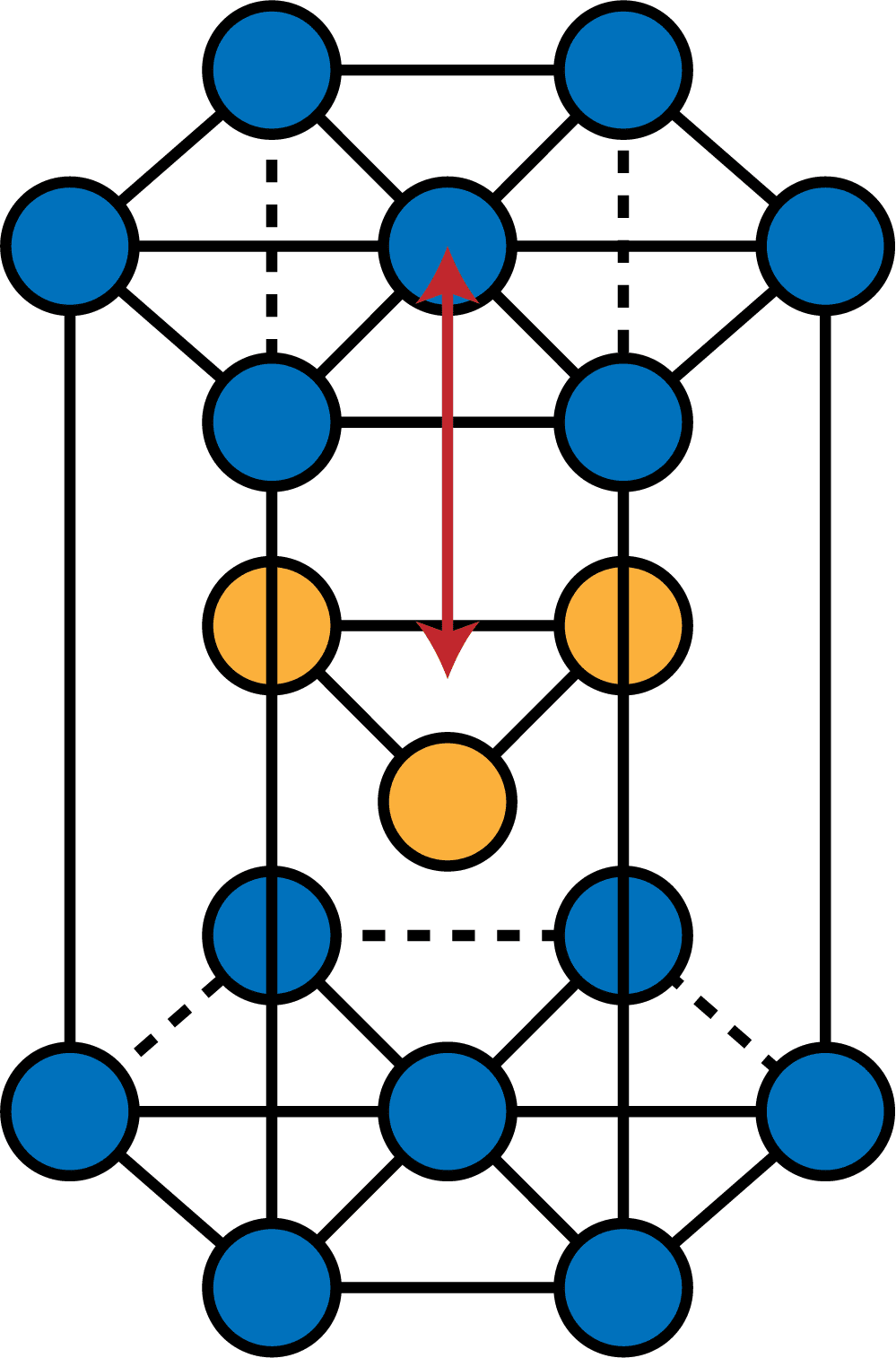
次に、六方最密構造から高さを求めるために必要な部分を取り出し、形を確認する。
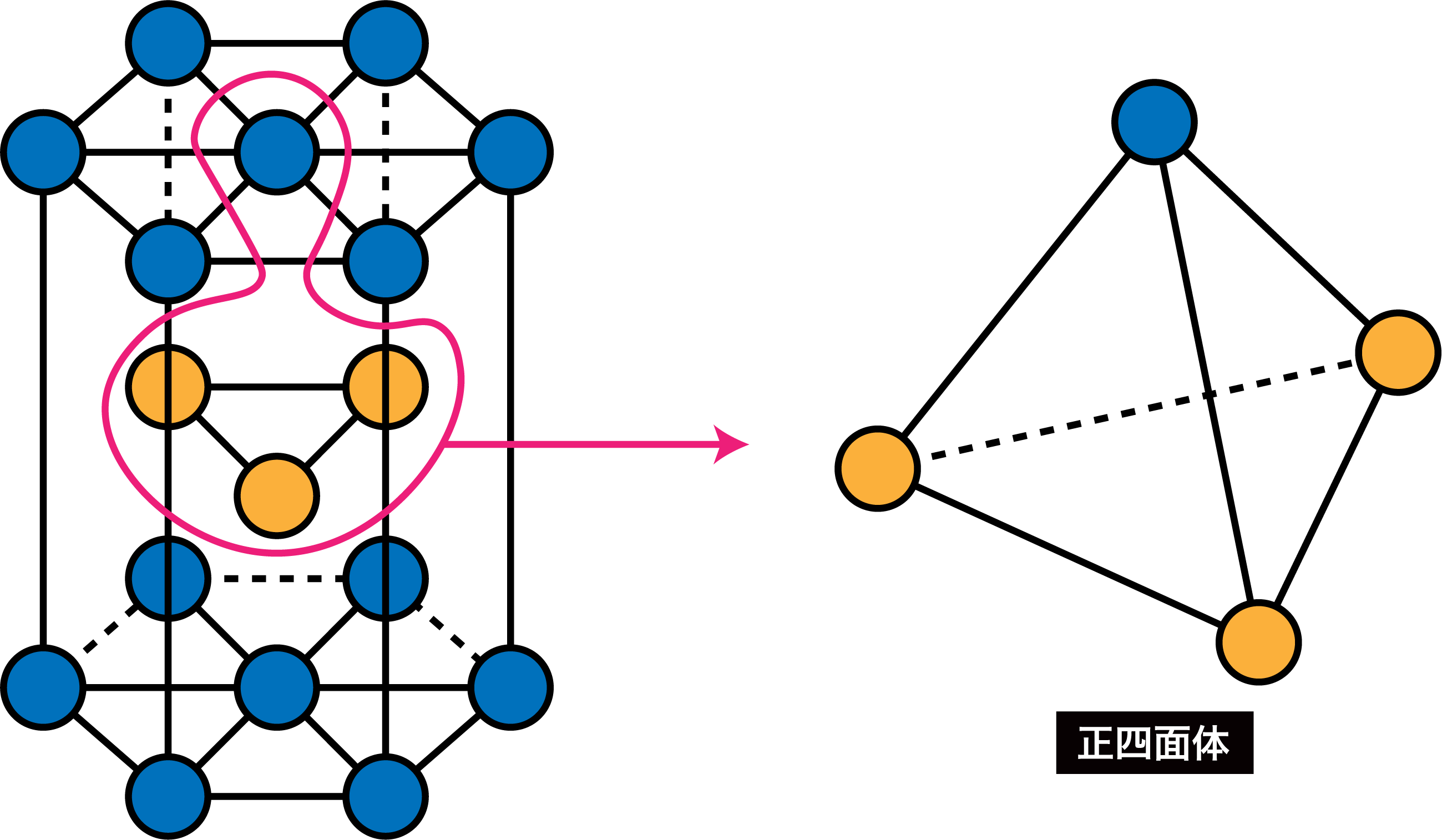
それぞれの原子にA〜Dの記号をふる。また、垂線を降ろした先は点Hとする。
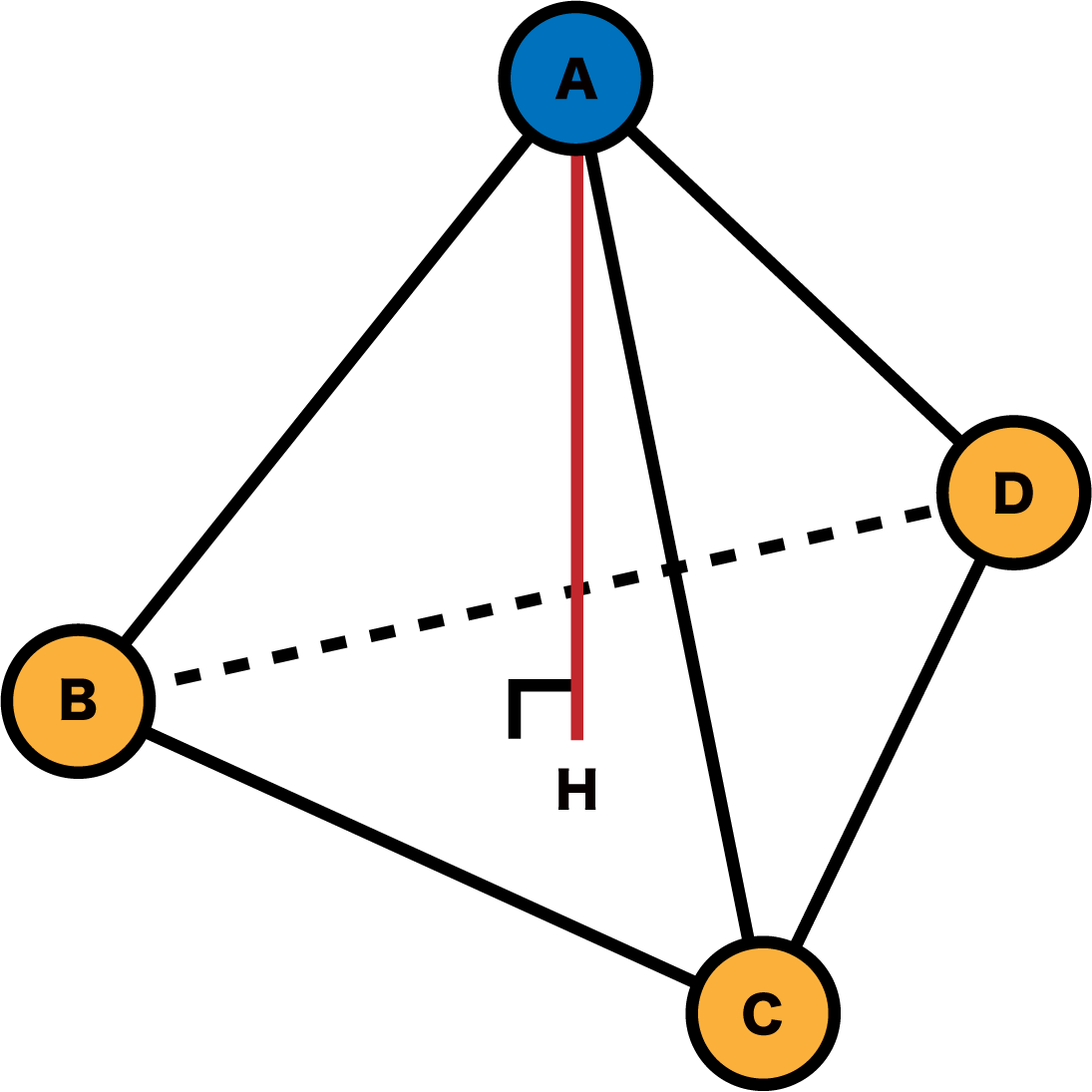
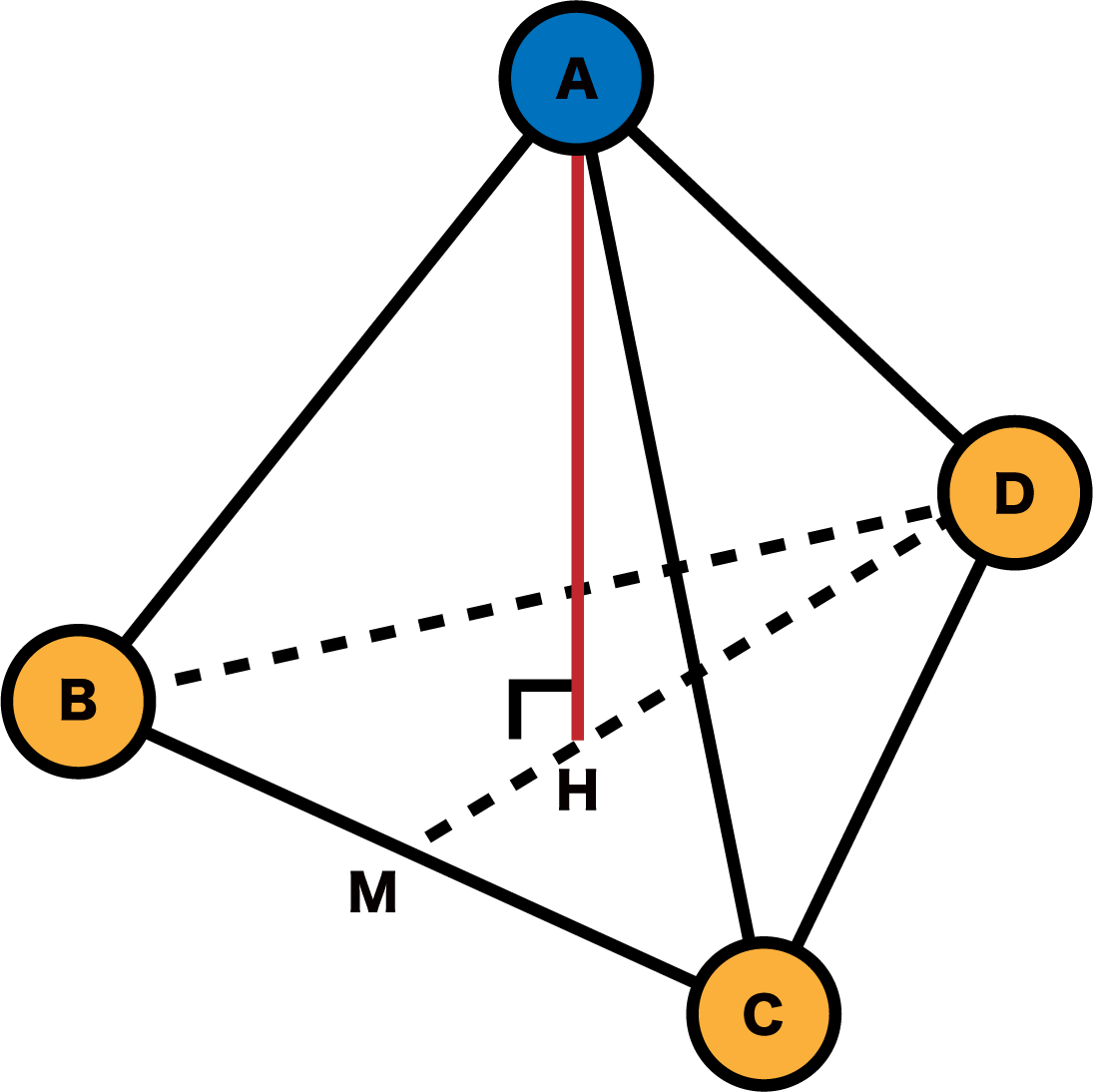
\[
\begin{align}&(2r)^{2}=(\mathrm{DM})^{2}+r^{2}\\
&\Leftrightarrow \mathrm{DM}=\sqrt{ 3 }r\end{align}
\]
CDの長さは2r、MCの長さはr(rは原子半径)のため、三平方の定理よりDとBCの中点Mの距離は√3rとなる。
正四面体の垂線の足であるHはこの立方体の“重心”である。
したがって、HはDMを2:1に内分する点のため(この辺は数学の知識)先ほどSTEP4で求めたDMの長さの2/3がDHの長さとなる。
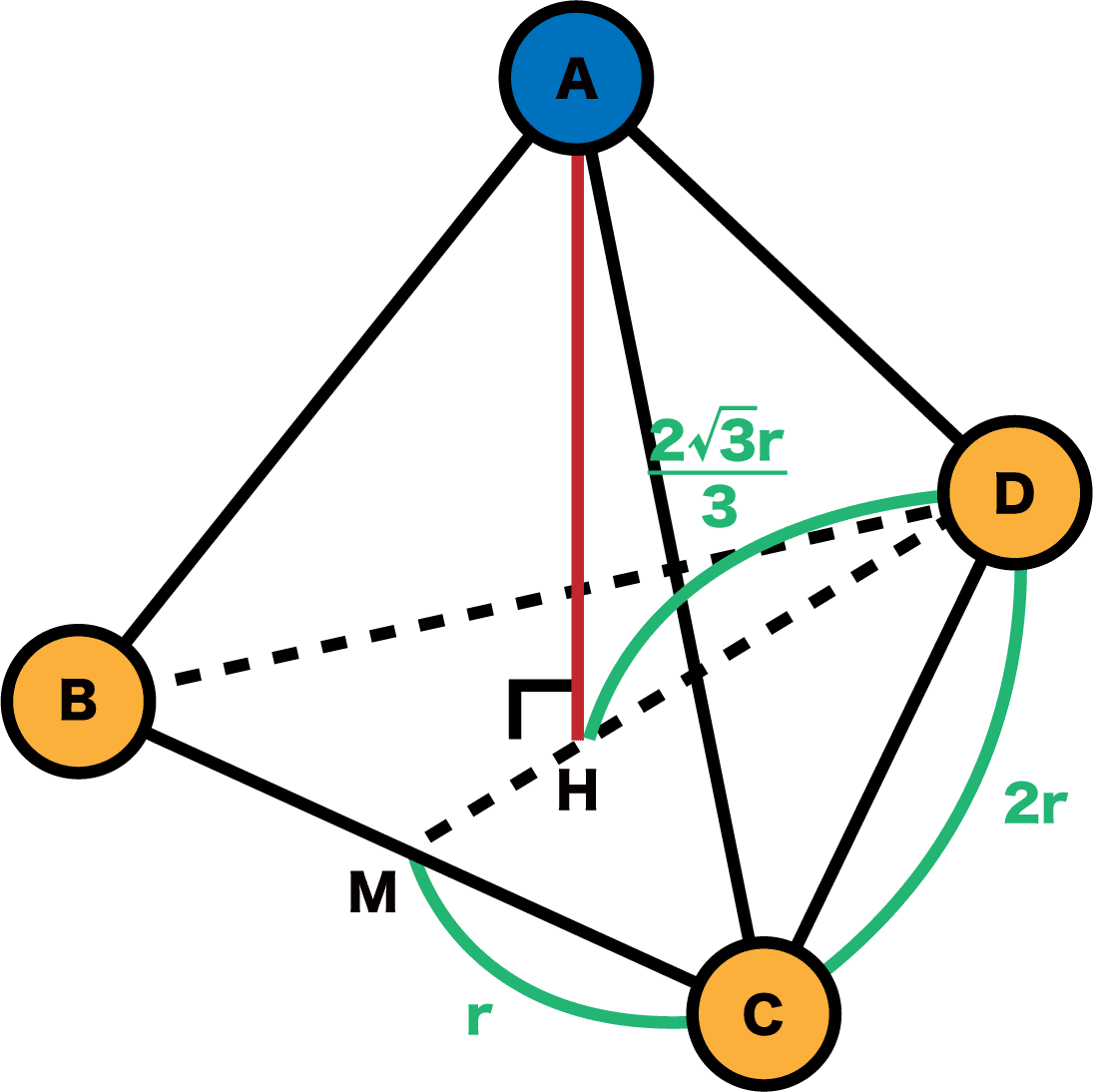
DM=√3rで、HはDMを2:1に内分する点のため…
\[
\begin{align}
\mathrm{DH} &=\sqrt{ 3 }r×\frac{ 2 }{ 2+1 }\\
&=\frac{ 2\sqrt{ 3 }r }{ 3 }
\end{align}
\]
STEP5で求めたDHの長さを使って、AHの長さを求める。
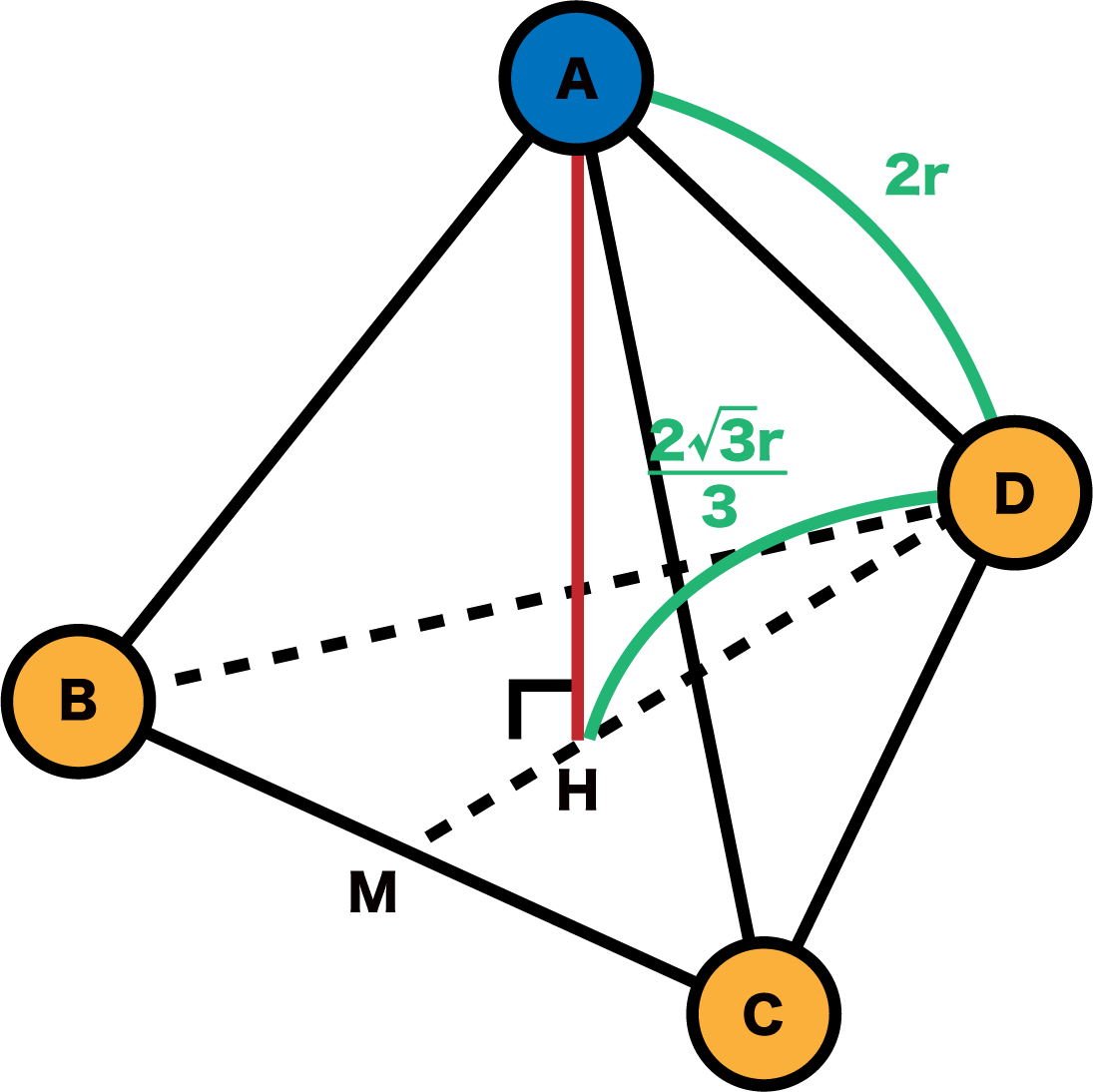
\[
\begin{align}&(2r)^{2}=(\mathrm{AH})^{2}+(\frac{ 2\sqrt{ 3 }r }{ 3 })^{2}\\
&\Leftrightarrow \mathrm{AH}=\frac{ 2\sqrt{ 6 }r }{ 3 }\end{align}
\]
AHの長さの2倍が六方最密構造全体の高さのため、この値を2倍する。
\[
\begin{align}
六方最密構造の高さ&=\underbrace{ \frac{ 2\sqrt{ 6 }r }{ 3 } }_{ \mathrm{AH}の長さ }×2\\
&=\frac{ 4\sqrt{ 6 }r }{ 3 }
\end{align}
\]
六方最密構造の充填率
- 単位格子の体積に占める原子の体積の割合を充填率という。
\[
充填率=\frac{ 原子の体積 }{ 単位格子の体積 }×100
\]
- 六方最密構造の充填率は3STEPで求める。
六方最密構造の充填率を求めるために、まずは六方最密構造の上層(下層)の表面積を求める。
六方最密構造の上層(下層)は正六角形であるため、次のように6個の正三角形に分けることができる。

この6個の三角形のうち1個の三角形の面積を求め、それを6倍することで上層(下層)の面積を求めることができる。

1つの三角形の高さ
\[
\begin{align}&(2r)^{2}=r^{2}+(高さ)^{2}\\
&\Leftrightarrow 高さ=\sqrt{ 3 }r\end{align}
\]
1つの三角形の面積
\[
2r×\sqrt{ 3 }r×\frac{ 1 }{ 2 }=\sqrt{ 3 }r^{2}
\]
六角形の面積
\[
\sqrt{ 3 }r^{2}×6=6\sqrt{ 3 }r^{2}
\]
次に、STEP1で求めた面積に六方最密構造の高さをかけることで六方最密構造の体積を出す。
\[
6\sqrt{ 3 }r^{2}×\underbrace{ \frac{ 4\sqrt{ 6 }r }{ 3 } }_{ 高さ }=24\sqrt{ 2 }r^{3}
\]
六方最密構造の体積は24√2r3となる(高さの求め方については上の「六方最密構造の高さの求め方と原子半径」を参照)。
最後に、公式を使って六方最密構造の充填率を求める。
\[
\begin{align}
充填率&=\frac{ 原子の体積 }{ 最密構造の体積 }×100\\
&=\frac{ \frac{ 4 }{ 3 }πr^{3}×6 }{ 24\sqrt{ 2 }r^{3} }×100\\
&=74(\%)
\end{align}
\]
最密構造の体積に関してはSTEP2で求めた値を使う。
また、球の体積は4/3πr3と表すことができる(これは数学の知識)ため、六方最密構造中に6個の原子が含まれる(上でやったように六方最密構造の1/3である単位格子中に含まれる原子の数が2個のため六方最密構造全体に含まれる原子の数は3倍の6個)ことを考えると、原子の体積の合計は4/3πr3×6となる。
以上より、六方最密構造の充填率は74%である。
六方最密構造の密度
- 六方最密構造の密度は『g/cm3』という単位で表される。
- この単位のうち、分子のgは六方最密構造に含まれる原子の重さを、分母のcm3は六方最密構造全体の体積を示している。
- したがって、アボガドロ定数をN(個/mol)、六方最密構造に含まれる原子の原子量をM(g/mol)とすると、六方最密構造の密度は次のように表すことができる。
\[
密度(\mathrm{g/cm^{3}})=\frac{ \frac{ M(\mathrm{g/mol}) }{ N(\mathrm{個/mol}) }×原子の数(個) }{ 24\sqrt{ 2 }r^{3}(\mathrm{cm^{3}}) }
\]
- ちなみに分子の部分は、原子量M(g/mol)をアボガドロ定数N(個/mol)で割ることで(molとmolが約分されて)「g/個」を出し、それに「原子の数(個)」をかけることで「g」を導き出している。
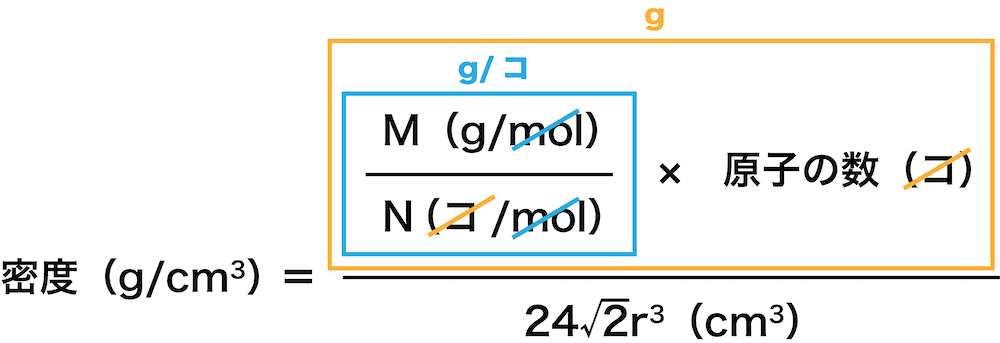
- あとはこの式に、アボガドロ定数である6.0×1023(個/mol)、六方最密構造に含まれる原子の数である6(個)、問題文で与えられている分子量(g/mol)、六方最密構造の体積(rには実際の値を入れる)を代入すれば、六方最密構造の密度を求めることができる。
六方最密構造まとめ
この『六方最密構造(単位格子に含む原子数・配位数・高さ・充填率の求め方など)』のページで解説した内容をまとめる。
- 六方最密構造に含まれる原子の数は2個である。
- 六方最密構造の配位数は12である。
- 六方最密構造の高さと原子半径の関係は次の通りである。
\[
六方最密構造の高さ=\frac{ 4\sqrt{ 6 }r }{ 3 }
\] - 六方最密構造の充填率は74%である。














