結晶とは（単位格子・配位数・密度・充填率など）

【プロ講師解説】このページでは『結晶（単位格子・配位数・密度・充填率など）』について解説しています。解説は高校化学・化学基礎を扱うウェブメディア『化学のグルメ』を通じて6年間大学受験に携わるプロの化学講師が執筆します。

結晶と単位格子

原子や分子、イオンなどの粒子が三次元的に規則正しく配列した固体を結晶という。

結晶内での粒子配列の構造を表したものを結晶格子といい、結晶格子で最小の繰り返し単位を単位格子という。

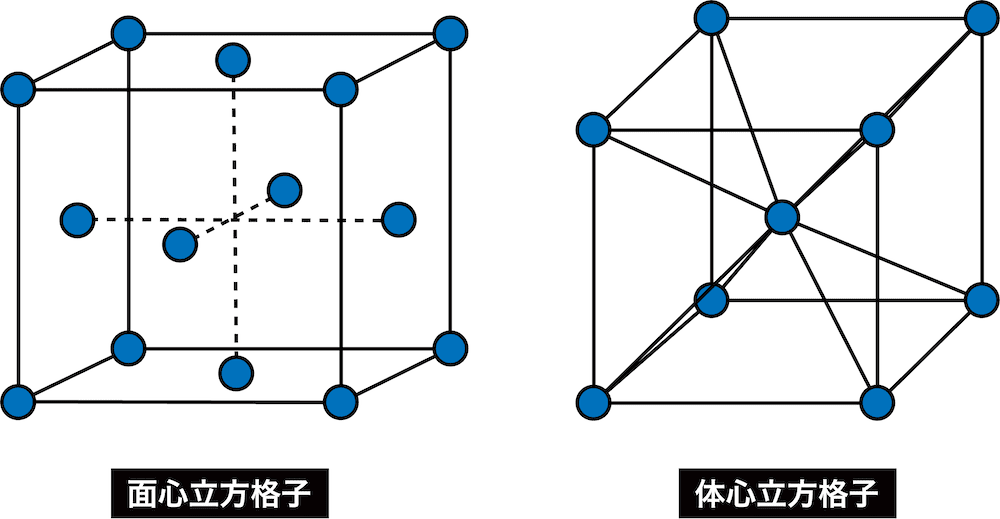
高校で学習する単位格子としては面心立方格子・体心立方格子などがある。

単位格子に含まれる粒子数

高校化学では単位格子内に含まれる粒子の数を聞かれる場合がある。

例えば、次の単位格子（体心立方格子）に含まれる粒子の数は合計2コである。

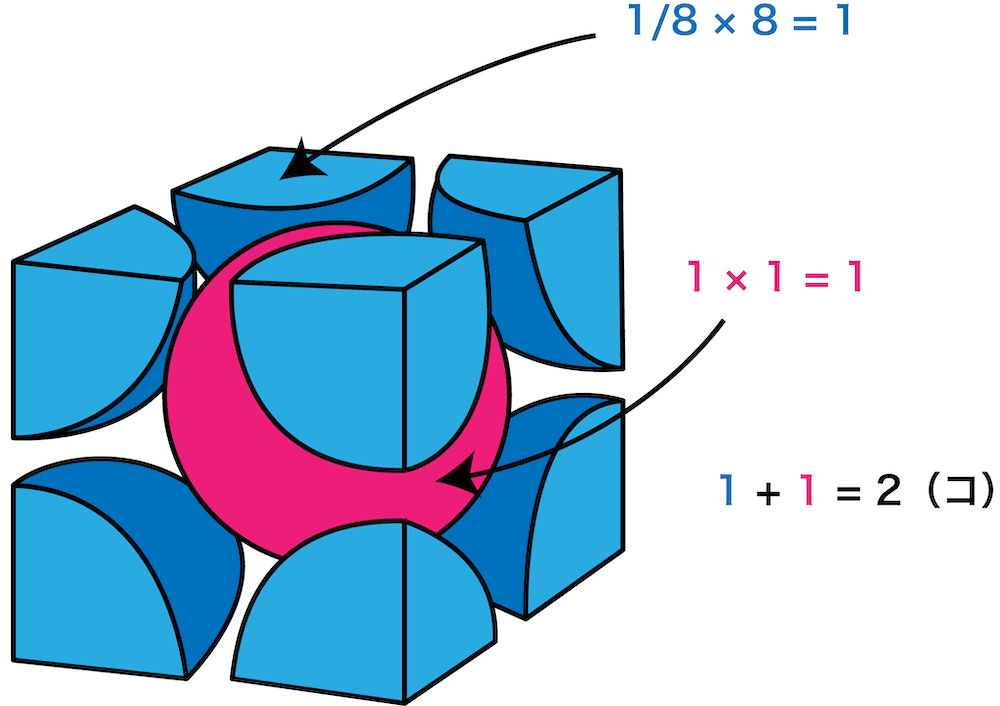
配位数

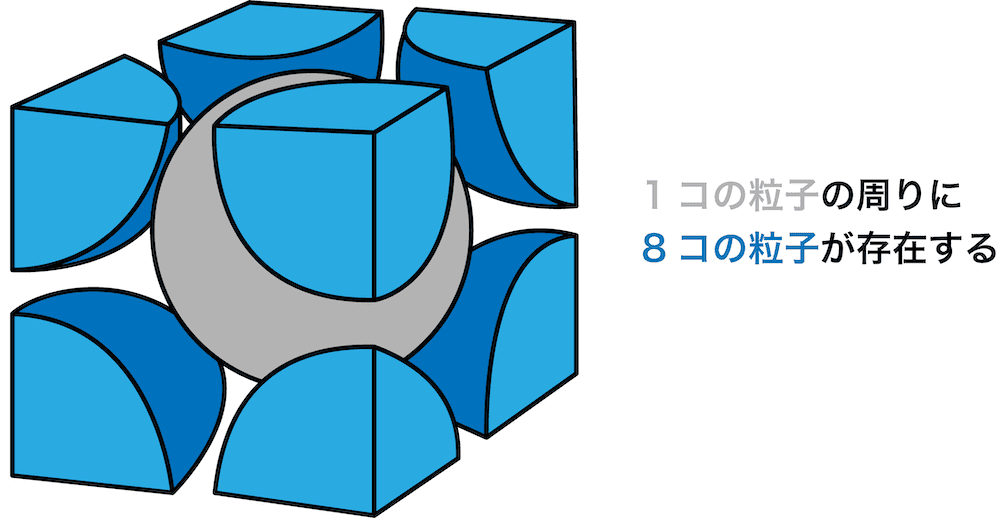
１コの粒子を取り囲む他の粒子の数を配位数という。

例えば、体心立方格子の配位数は8である。

格子定数と原子半径

単位格子の1辺の長さを格子定数という。

体心立方格子を斜めに割ると次のようになる。（原子半径をr、格子定数をaとする）

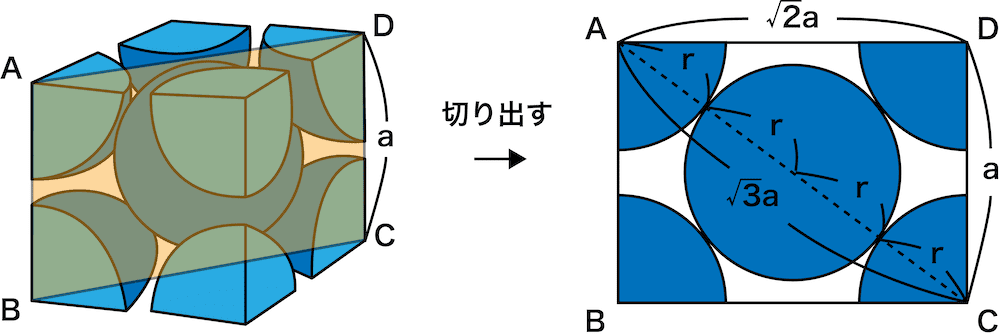
辺DC（AB）の長さはa、辺AD（BC）の長さは√2aなので、三平方の定理によりrが４つ並んでいる部分（AC,DB）が√3aであることがわかる。
したがって、体心立方格子の格子定数と原子半径の関係は以下のようになる。

\[
4r=\sqrt{ 3 }a\\
\Leftrightarrow r=\frac{ \sqrt{ 3 } }{ 4 }a
\]

充填率

単位格子の体積に占める粒子の体積の割合を充填率といい、次の式で求めることができる。

\[
充填率 = \frac{ 粒子の体積 }{ 単位格子の体積 }×100
\]

例えば、体心立方格子の充填率は次のようになる。（球の体積は4/3πr³、上述の通り単位格子の格子定数と粒子半径rとの関係はr=√3×a/4）

\[
\begin{align}
充填率&=\frac{ 原子の体積 }{ 単位格子の体積 }×100\\
&=\frac{ \frac{ 4 }{ 3 }πr^{3}×2 }{ a^{3} }×100\\
&=\frac{ \frac{ 4 }{ 3 }π(\frac{ \sqrt{ 3 } }{ 4 }a)^{3}×2 }{ a^{3} }×100\\
&=\frac{ \sqrt{ 3 }π }{ 8 }×100\\
&≒68(\%)
\end{align}
\]

密度

単位格子の密度は次の式で求めることができる。

\[
\begin{align}
密度(g/cm^{3}) &= \frac{ 単位格子の質量(g) }{ 単位格子の体積(cm^{3}) }\\
&=\frac{ \frac{ M(g/mol) }{ N(コ/mol) }×原子の数(コ) }{ a^{3}(cm^{3}) }
\end{align}
\]

ちなみに、単位格子は結晶の最小繰り返し単位なので、単位格子の密度は結晶の密度と同じであるということも押さえておこう。

結晶とは（単位格子・配位数・密度・充填率など）

結晶と単位格子

単位格子に含まれる粒子数

配位数

格子定数と原子半径

充填率

密度

関連：計算ドリル、作りました。