MENU
ヨウ素価とは(計算問題・けん化価との違いなど)
目次
はじめに
【プロ講師解説】このページでは『ヨウ素価とは(計算問題・けん化価との違いなど)』について解説しています。
ヨウ素価とは
- 油脂100gに付加するヨウ素のg数をヨウ素価という。
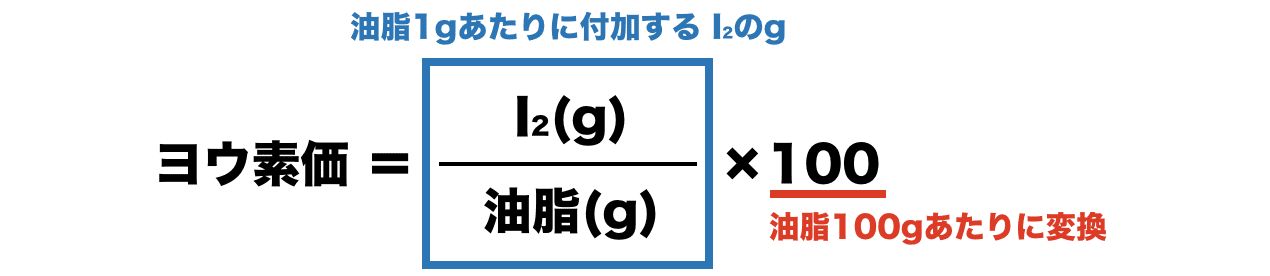
ヨウ素価を求める計算
- ここで、油脂1分子に含まれる二重結合(C=C)の数をa個とすると、付加反応は次のように考えることができる。

- この反応において、油脂1molに対してI2がamol必要なので、油脂の分子量をM(g/mol)とするとヨウ素価は次のように表すことができる。
\[ \begin{align}
ヨウ素価&\mathrm{=\frac{ I_{ 2 }(g)}{ 油脂(g) }×100}\\
&=\frac{ \mathrm{a(mol)×254(g/mol)} }{ \mathrm{1(mol)×}M\mathrm{(g/mol)} }×100\\
&=\frac{ 2.54\mathrm{a}×10^{4} }{ \mathrm{M} }
\end{align} \]
- それではこの式を使って次の例題を解く。
問題
分子量878、二重結合の数が6個の油脂のヨウ素価を求めよ。
- 問題文で油脂の分子量と二重結合の数が与えられているため、それらを先ほどのヨウ素価の式に代入する。
\[ \begin{align}
ヨウ素価&=\frac{ 2.54\mathrm{a}×10^{4} }{ M }\\
&=\frac{ 2.54×6×10^{4} }{ 878 }\\
&≒174
\end{align} \]
- ヨウ素価は174となる。
ヨウ素価の式をもう一度確認しましょう。
\[ヨウ素価=\frac{ 2.54a×10^{4} }{ M }\]
式から分かるように、ヨウ素価は油脂の”二重結合”の数に”比例”し、”分子量”に”反比例”します。けん化価が油脂の”分子量”に”反比例”することと合わせて正確に覚えておきましょう。
参考:けん化価とは(計算問題・ヨウ素価との違いなど)














