浸透圧（公式・単位・計算問題・求め方・ファントホッフの法則）

2018年11月7日2023年6月23日

はじめに

【プロ講師解説】このページでは『浸透圧（公式・単位・計算問題・求め方・ファントホッフの法則）』について解説しています。

半透膜とは

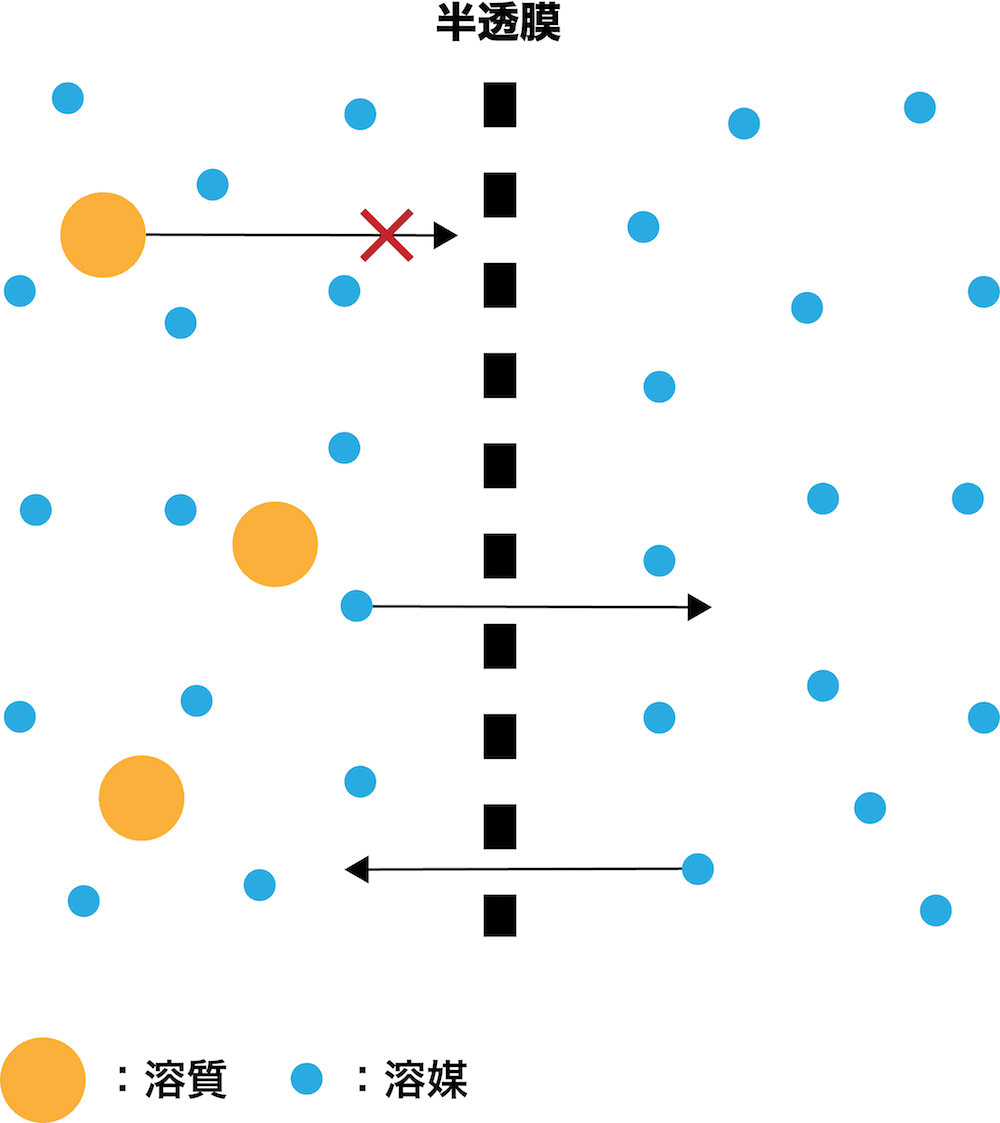
小さい物質だけを通し大きい物質は通さない膜を半透膜という。
浸透圧の単元では基本的に半透膜＝溶媒分子だけを通し溶質分子は通さない膜として扱われる。

浸透とは

V字型の容器を半透膜で区切り、片方に水、もう片方にデンプン水溶液を入れる。

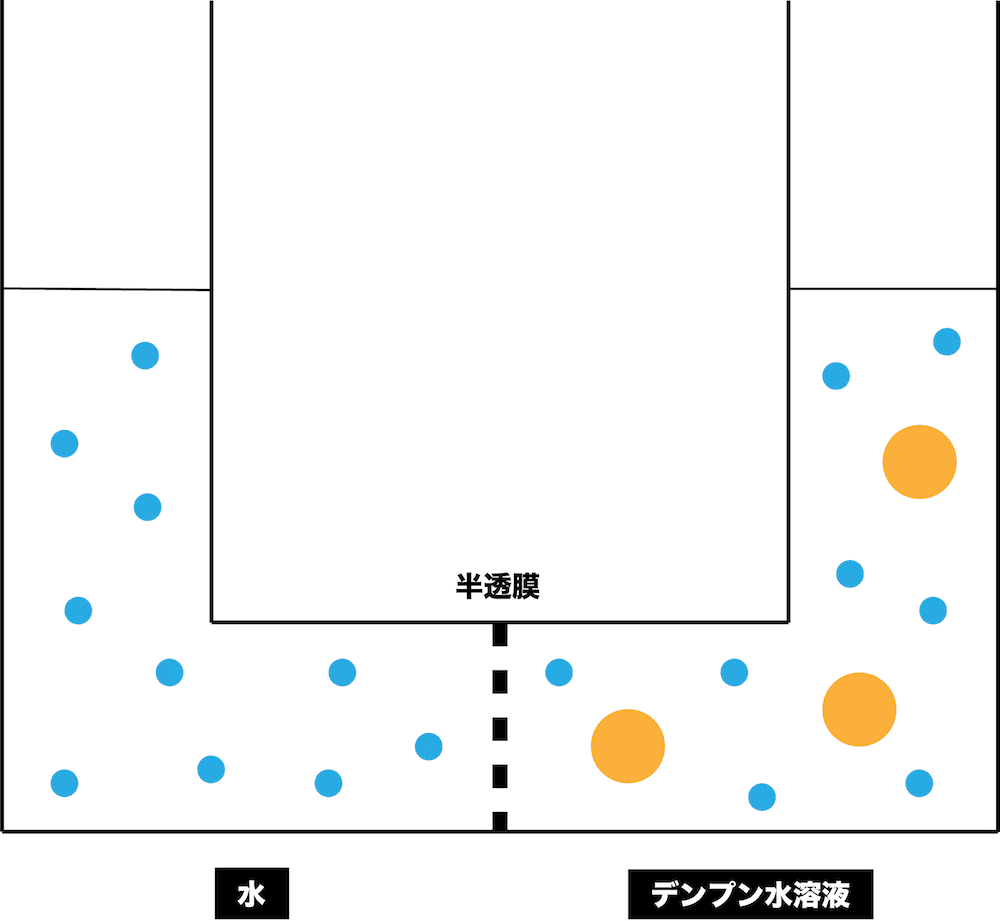
これをしばらく放置すると、次のようになる。

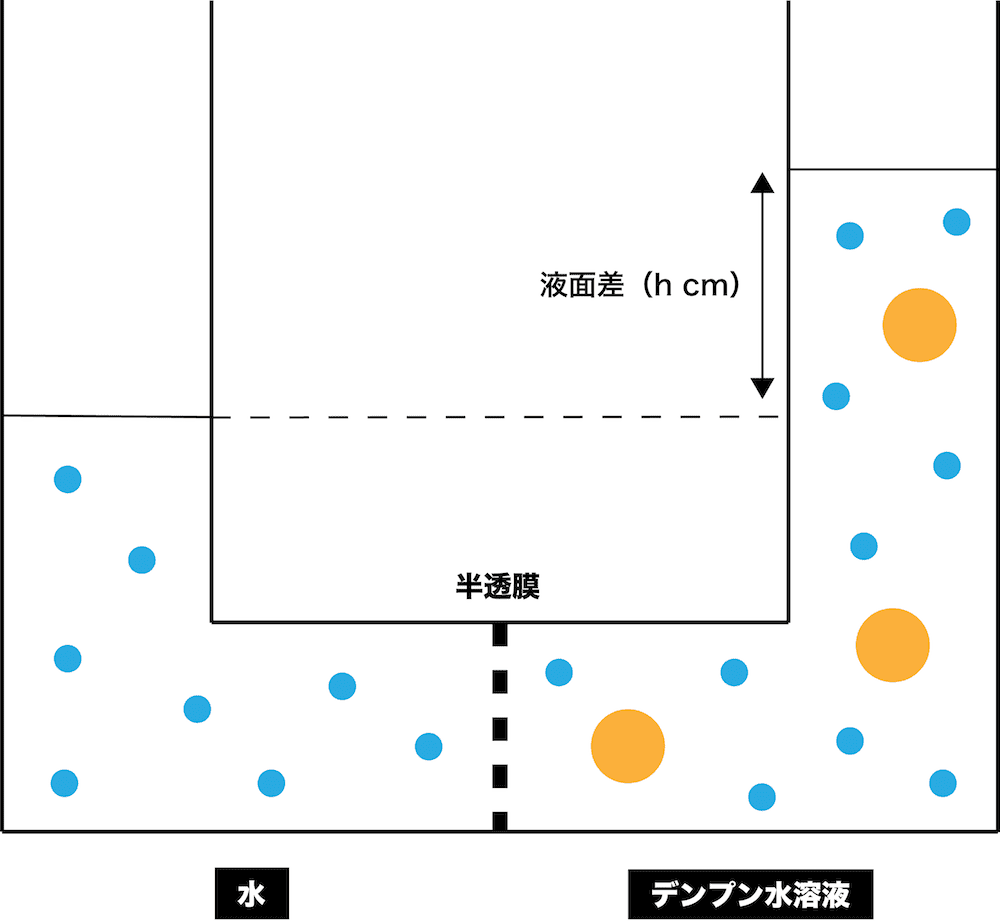
水（濃度の小さい方）がデンプン水溶液（濃度の大きい方）側に流れ込み、濃度差を無くそうとする。この現象を浸透という。
ちなみに、浸透が起こった結果、水の液面は下がりデンプン水溶液の液面は上がる。

浸透圧とは

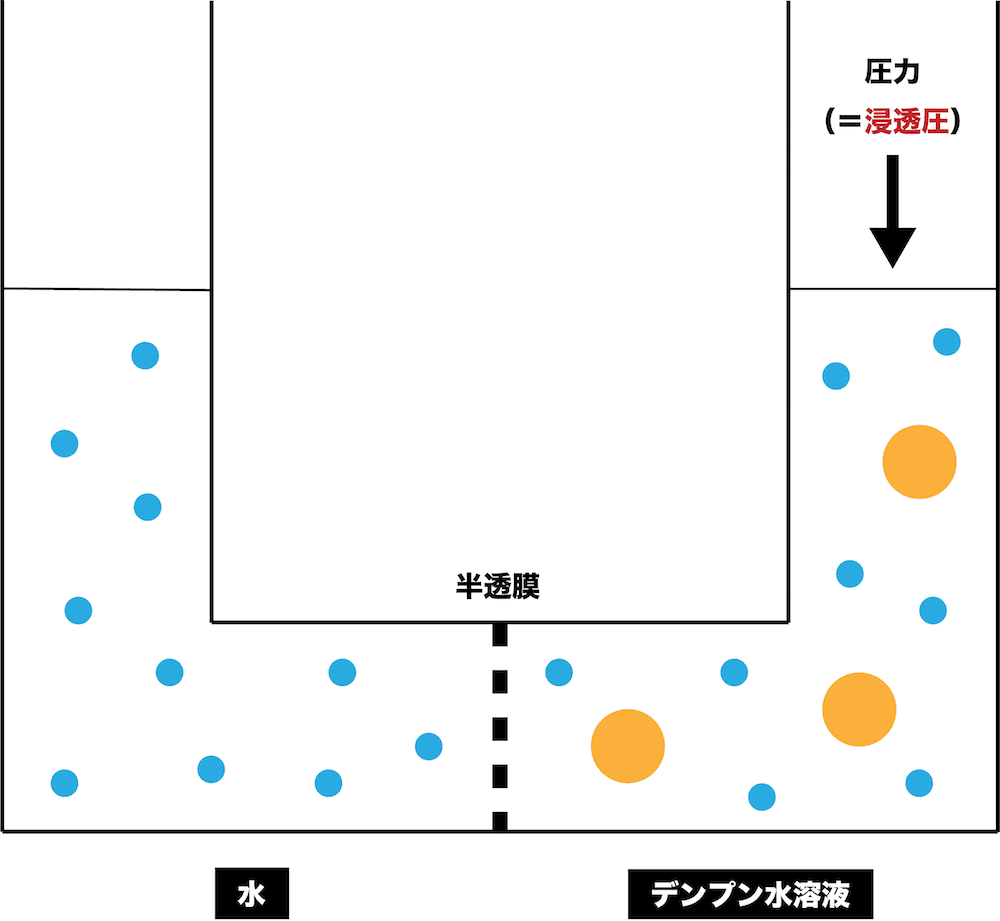
先ほどの図をもう一度確認する。

このように“浸透”が起こって左右で液面差ができているとき、液面が高い方に一定の圧力を加えることで液面差をなくすことができる。このときに加える圧力を浸透圧という。

浸透圧の公式「ファントホッフの法則」

浸透圧を使った計算問題を解く前準備として、ファントホッフの法則を覚えておく必要がある。

●ファントホッフの法則

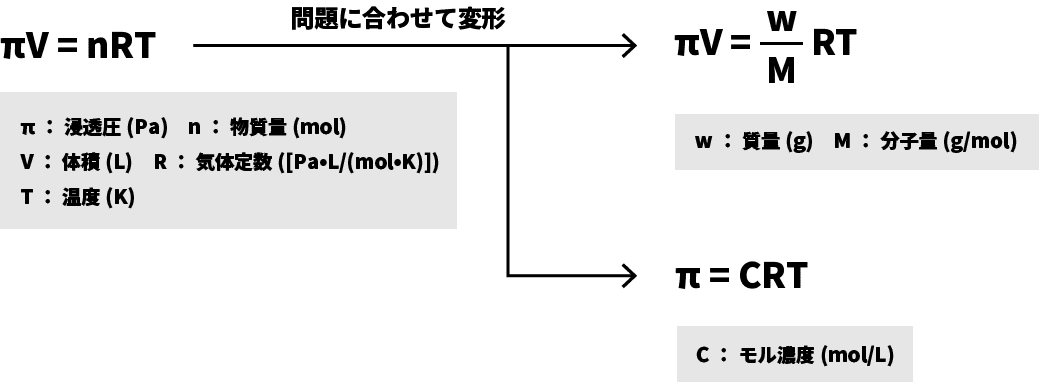
気体の状態方程式の圧力Pが浸透圧πに置き換わったイメージである。
左の式がベースで、問題に合わせて右の2つの式に変形して用いることもある。

浸透圧の計算問題の解き方

浸透圧を使った計算問題の解き方について、例題を用いて解説する。

モル濃度を用いて浸透圧を求める問題

問題

27℃において、0.32mol/LのグルコースC₆H₁₂O₆水溶液の浸透圧は何Paか。ただし、グルコースは電離せず、各原子の原子量はH=1、C=12、0＝16とする。

ファントホッフの法則の式（π=CRT）に問題文で与えられている数値を代入すると、次のようになる。

\[ \begin{align} π &= CRT \\
&=0.32×8.3×10^{3}×(27+273) \\
&≒8.0×10^{5}(\mathrm{Pa}) \end{align} \]

質量を用いて浸透圧を求める問題

問題

27℃において、34.2gのスクロースC₁₂H₂₂O₁₁を水に溶かして500mLとした。この水溶液の浸透圧は何Paか。ただし、スクロースは電離せず、各原子の原子量はH=1、C=12、0＝16とする。

ファントホッフの法則の式（πV=w/M×RT）に問題文で与えられている数値を代入すると、次のようになる。

\[ \begin{align}πV &= \frac{ w }{ M }RT \\
\leftrightarrow π &=\frac{ wRT }{ MV } \\
&=\frac{ 34.2×8.3×10^{3}×(27+273) }{ 342×0.5 } \\
&≒5.0×10^{5}(\mathrm{Pa}) \end{align} \]

電解質の浸透圧を求める問題

問題

塩化カルシウムCaCl₂を3.33g量り取り、これを水に溶かして半透膜で仕切ったU字管に入れ、200mLの溶液を調整した。27℃のときにこの溶液の浸透圧は何Paか。ただし、塩化カルシウムは完全電離し、各原子の原子量はCl=35.5、Ca=40とする。

ファントホッフの法則の式（πV=nRT）に問題文で与えられている数値を代入すると、次のようになる。

\[ \begin{align}πV &= nRT \\
\leftrightarrow π &=\frac{ nRT }{ V } \\
&=\frac{ \frac{ 3.33 }{ 111 }×3×8.3×10^{3}×(27+273) }{ 0.2 } \\
&≒1.1×10^{6}(\mathrm{Pa}) \end{align} \]

nの値（3.33/111）に3を掛けているのは、塩化カルシウムが電解質であり、次のように電離して1molのCaCl₂から3molのイオンが生成するためである。

\[ \mathrm{CaCl_{2}→Ca^{2+}+2Cl^{-}} \]

血液のモル濃度を求める問題

問題

人の血液の浸透圧は37℃（体温付近）で7.5×10⁵Paである。この血液中の溶質のモル濃度（mol/L）を求めよ。

ファントホッフの法則の式（π=CRT）に問題文で与えられている数値を代入すると、次のようになる。

\[ \begin{align}π &= CRT \\
\leftrightarrow C &=\frac{ π }{ RT } \\
&=\frac{ 7.5×10^{5} }{ 8.3×10^{3}×(37+273) } \\
&≒0.29(\mathrm{mol/L}) \end{align} \]

生食の調製に必要な塩化ナトリウム(g)を求める問題

問題

上の血液と同じ浸透圧の生理食塩水500mLを調整するために、同じ条件で何gの塩化ナトリウムNaClを用いればよいか。ただし、塩化ナトリウムは完全電離し、各原子の原子量はNa=23、Cl=35.5とする。

病院で頻繁に使われる生理食塩水（生食）は、人の血液に近い浸透圧である場合が多い。生食絡みの計算は医療関係の学部でよく出るので、そういった学部を受ける人はしっかりできるようにしておこう。
π、R、Tが一定のとき、ファントホッフの法則の式（π=CRT）より、C=一定となる。

\[ \begin{align}π&=CRT\\
↔︎C&=\underbrace{ \frac{ π }{ RT } }
_{ \text{ 一定 }}\\
↔︎C_{1}&=C_{2}\end{align} \]

したがって、血液のモル濃度（mol/L）と生理食塩水のモル濃度（mol/L）をイコールで結び式をつくると、次のようになる。

\[ \begin{align}&\underbrace{ 0.29(\mathrm{mol/L}) }_{ 血液 } =\underbrace{ \frac{ \frac{ x(\mathrm{g}) }{ 58.5(\mathrm{g/mol}) }×2 }{ 0.5(\mathrm{L}) } }_{ 生理食塩水 }\\
&\therefore x≒4.2(\mathrm{g}) \end{align}\]

水銀柱が絡んだ問題-浸透圧の計算問題

問題

ある非電解質を半透膜で仕切ったU字管の片側に溶解させ、生じた液面差を測定すると27℃で14.5cmだった。この液面差に相当する浸透圧を求めよ。ただし、水銀の密度を13.6g/cm³、水溶液の密度を1.1g/cm³とし、1.0×10⁵Pa=76cmHgとする。

水銀柱が絡んだ浸透圧問題はやや難しいが、一度やり方を覚えてしまえば意外と簡単なのでぜひこの機会に押さえておこう。
まず、Hg柱のおける液面の高さをa(cm)として式をたてる。

\[ \begin{align}&\underbrace{1.1(\mathrm{g/cm^{3}})×6.5(\mathrm{cm}) }_{ 水溶液中の圧力 } =\underbrace{ 13.6(\mathrm{g/cm^{3}})×a(\mathrm{cm}) }_{ \mathrm{Hg}柱の圧力 }\\
&\therefore a=\frac{ 7.15 }{ 13.6 }\end{align}
\]

次に、比の関係を用いて浸透圧πを求める。

\[ \begin{align}&1.0×10^{5}(\mathrm{Pa})：76(\mathrm{cmHg})=π(\mathrm{Pa})：\frac{ 7.15 }{ 13.6 }(\mathrm{cmHg})\\
&\therefore π=\frac{ 7.15 }{ 13.6×76 }×10^{5}(\mathrm{Pa}) \end{align}\]