MENU
ラウールの法則と蒸気圧降下
目次
はじめに
【プロ講師解説】このページでは『ラウールの法則と蒸気圧降下(グラフや各種用語など)』について解説しています。
蒸気圧降下度
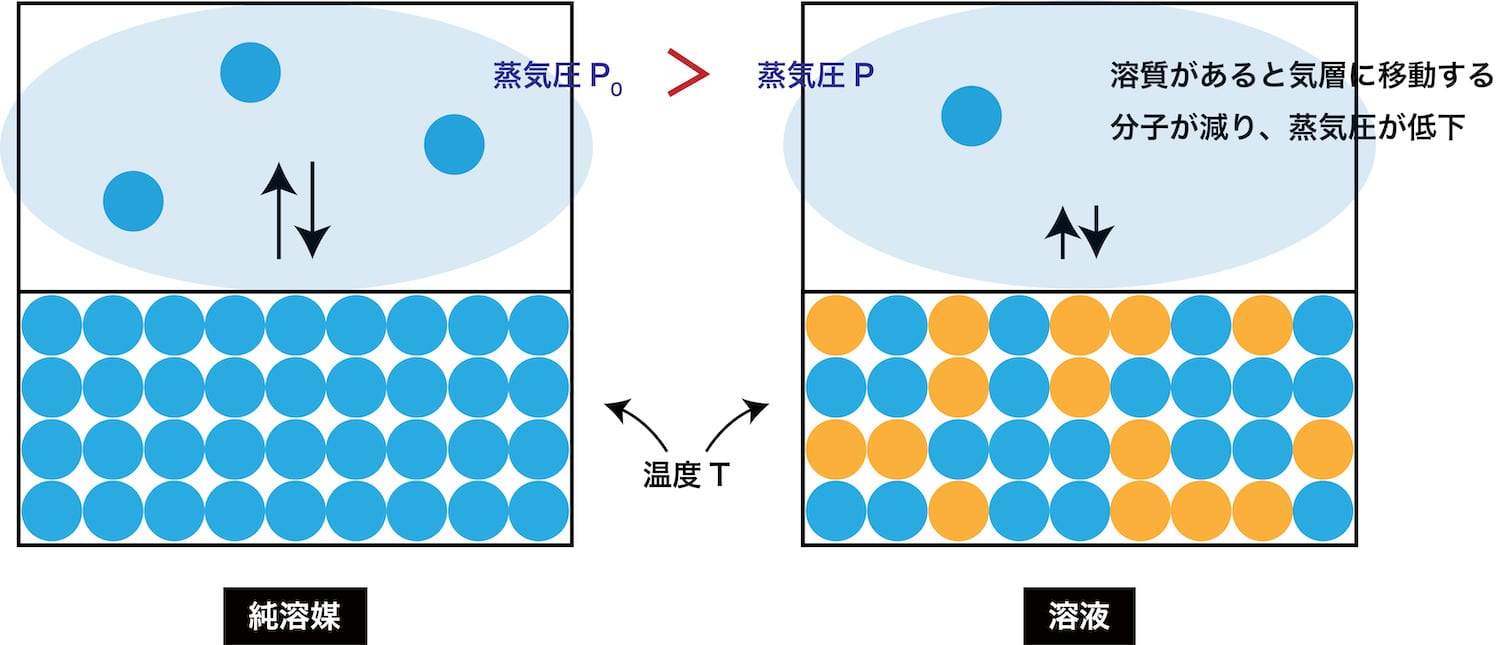
- 純溶媒と溶液の蒸気圧の差である蒸気圧降下度ΔPは次のように表すことができる。
\[ ΔP=P_{0}-P \]
- ここで(溶媒分子の物質量N、溶質粒子の物質量をnとして)先ほどのラウールの法則P=P0×X媒を用いると、次のような式を導くことができる。
\[ \begin{align} ΔP&=P_{0}-P\\
&=P_{0}-(P_{0}×X_{媒})\\
&=P_{0}(1-X_{媒})\\
&=P_{0}(1-\frac{ N }{ N+n })\\
&=P_{0}・\underbrace{ \frac{ n }{ N+n } }
_{ \text{ 溶質のモル分率 }}
\end{align} \]
- 希薄溶液では、溶媒分子数が溶質粒子数より大幅に多いため、N+n≒Nと近似できる。
\[ \begin{align} ΔP&=P_{0}・\underbrace{ \frac{ n }{ N+n } }
_{ \text{ 溶質のモル分率 }}\\
&≒P_{0}・\frac{ n }{ N }
\end{align} \]
- ここで、溶媒の分子量をM媒、溶質の質量モル濃度をm(mol/kg)とすると、次のようになる。
\[ \begin{align} ΔP&=P_{0}・\frac{ n }{ N・\color{red}{M_{媒}×10^{-3}} }・\color{red}{M_{媒}×10^{-3}}\\
&≒P_{0}・M_{媒}×10^{-3}・\underbrace{ \frac{ n }{ N・M_{媒}×10^{-3} } }
_{ \text{ 質量モル濃度(mol/kg) }}\\
&=P_{0}M_{媒}×10^{-3}×m
\end{align} \]
- P0M媒×10ー3は溶媒に固有な値なので、定数Kとおく。
\[ ΔP=K×m \]
質量モル濃度に関する補足
- 次中の質量モル濃度mについて、補足的な説明を行う。
\[ ΔP=K×m \]
- 質量モル濃度の定義は次の通りである。
\[ 質量モル濃度(\mathrm{mol/kg}) = \frac{ 溶質(\mathrm{mol}) }{ 溶媒(\mathrm{kg}) } \]
- この式における”溶質のmol数”には、3パターン存在する。
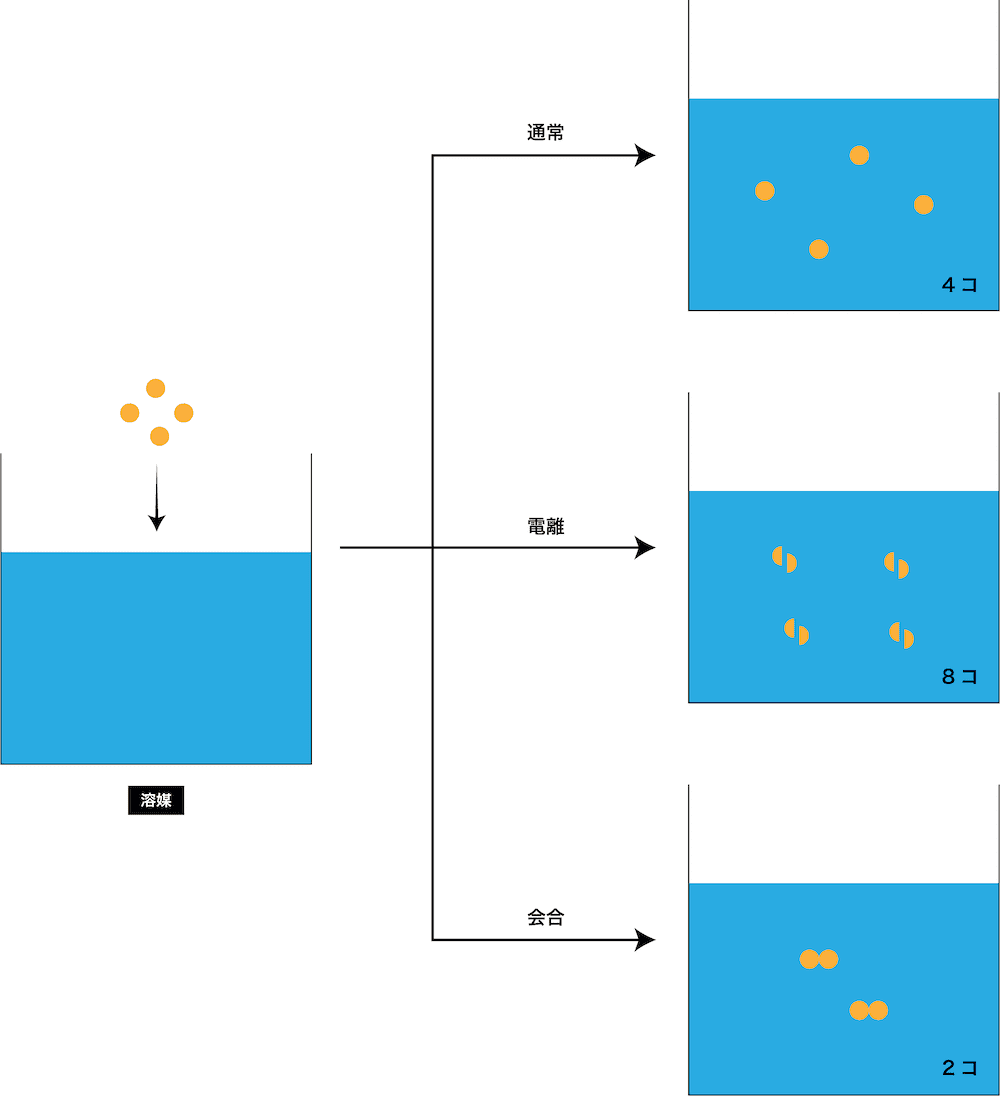
- 1番上はグルコース水溶液など非電解質水溶液の場合、2番目は塩化ナトリウム水溶液など電解質水溶液の場合、3番目はベンゼンを溶媒にして酢酸分子を溶かした溶液などの場合である。
- 塩化ナトリウム水溶液の場合は電離するので溶質のmol数を2倍、ベンゼンを溶媒にして酢酸分子を溶かした溶液の場合は二量体を形成するので溶質のmol数を1/2倍する必要がある。
蒸気圧降下のグラフ
- 水の状態図は次の通りである。

- 水にブドウ糖などの溶質を溶解させると、状態図は次のようになる。
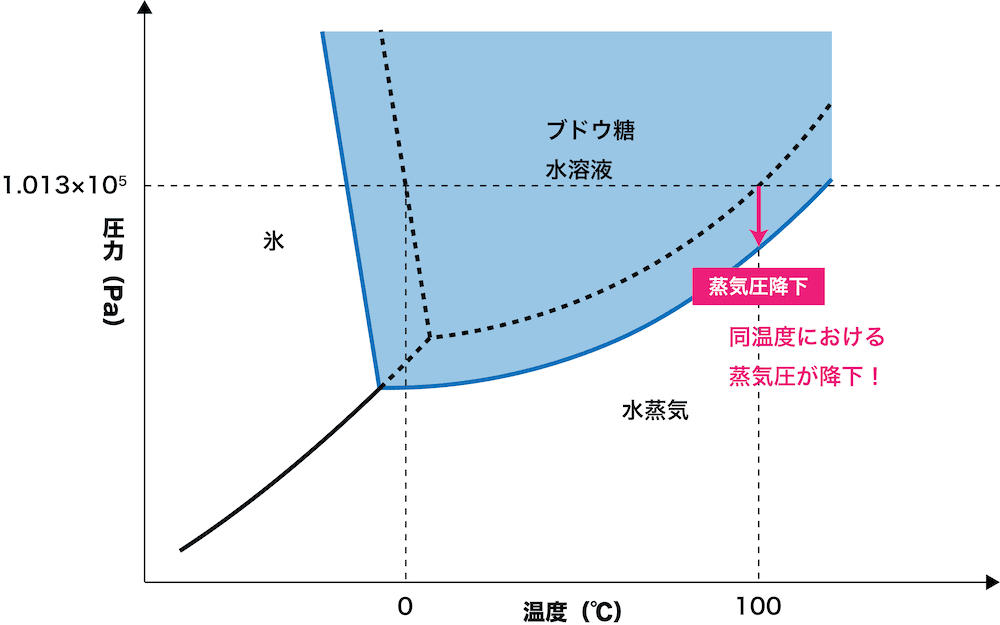
- グラフより、溶媒に溶質としてブドウ糖(グルコース)を加えた溶液は、純水と比べて同一温度における蒸気圧が下がっていることが確認できる。