MENU
面心立方格子【高校化学・化学基礎一問一答】
次のように、立体の各頂点と各面の中心に同種の粒子が配列された結晶格子を【1】という。
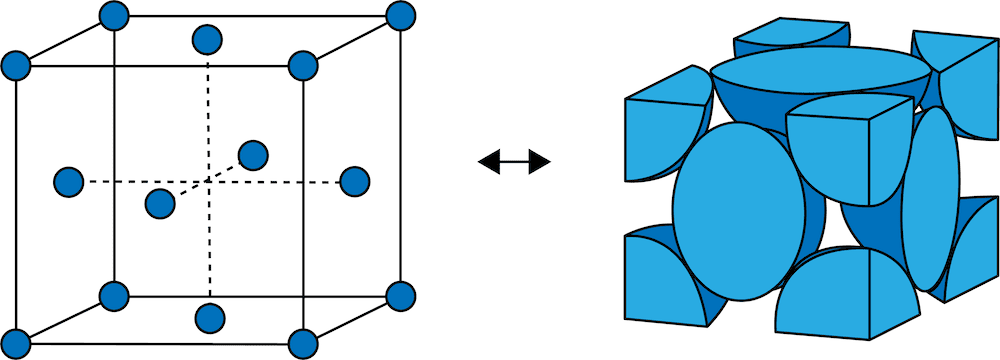
解答/解説:タップで表示
面心立方格子に含まれる原子の数は【1】個である。
解答/解説:タップで表示
解答:【1】4
面心立方格子に含まれる原子の数を考える。

面心立方格子に含まれる原子のうち、格子の各“頂点”にあるものは原子を8分割した状態になっている。

8分割(1/8)したものが頂点の数分=8個あるため、頂点にある原子の数は合わせて1個である。
\[
\frac{ 1 }{ 8 }×8=1
\]
次に、面心立方格子の各“面”に存在する原子の数を数える。
格子の6面(横に4面上下に1面ずつ)にある原子は球体の原子を2分割したものになっている。
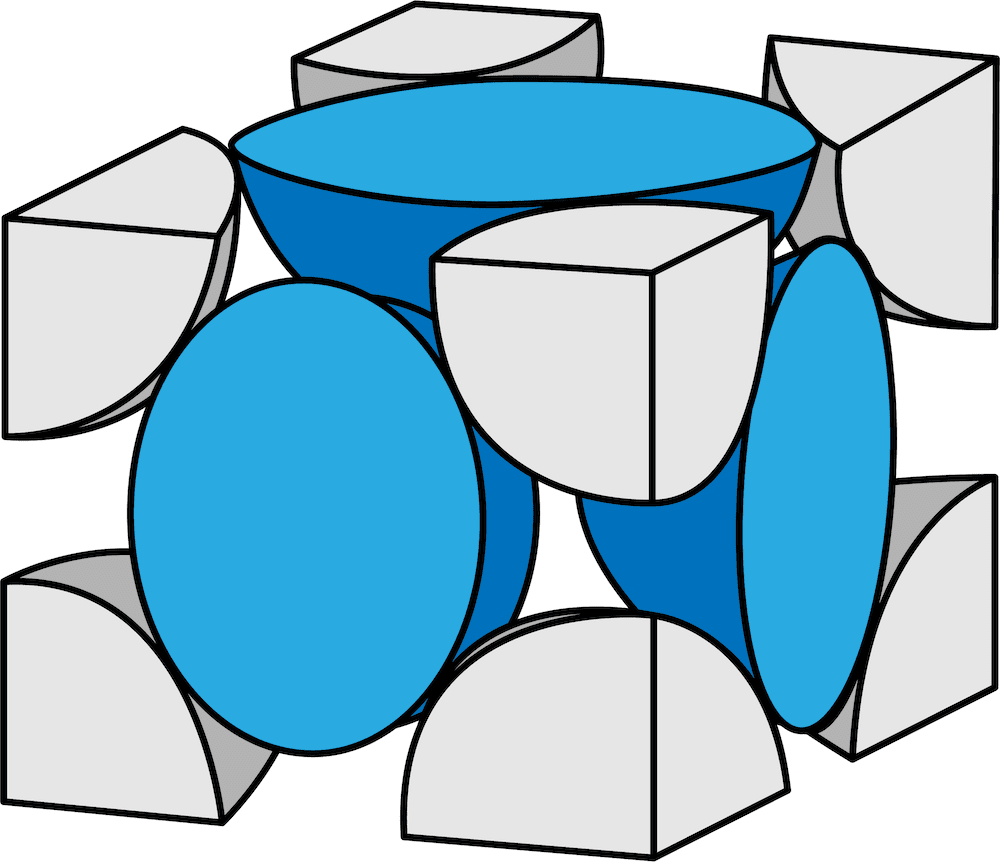
2分割(1/2)したものが各面の数分=6個あるため、面にある原子の数は合わせて3個である。
\[
\frac{ 1 }{ 2 }×6=3
\]
以上より、面心立方格子に含まれる原子の数は4個である。
\[
\underbrace{ 1 }_{ 頂点 }+\underbrace{ 3 }_{ 面 }=4
\]
面心立方格子の配位数は【1】である。
解答/解説:タップで表示
解答:【1】12
面心立方格子を2個つなぎ合わせると、次のようになる。

中心の部分で、左側の単位格子に含まれる原子(1/2のもの)と右側の単位格子に含まれる原子(1/2のもの)が合わさって、1個の球状の原子が出来上がっている。
配位数とは「1個の原子を取り囲む他の粒子の数」のことなので、図から面心立方格子の配位数は12であることがわかる。
面心立方格子の格子定数aと原子半径rの関係は次の通りである。
\[ \mathrm{r=\frac{ \sqrt{ 【1】 } }{ 4 }a} \]
解答/解説:タップで表示
解答:【1】2
単位格子の1辺の長さを格子定数という。
面心立方格子の側面だけをみると次のようになっている(原子半径をr、格子定数をaとする)。
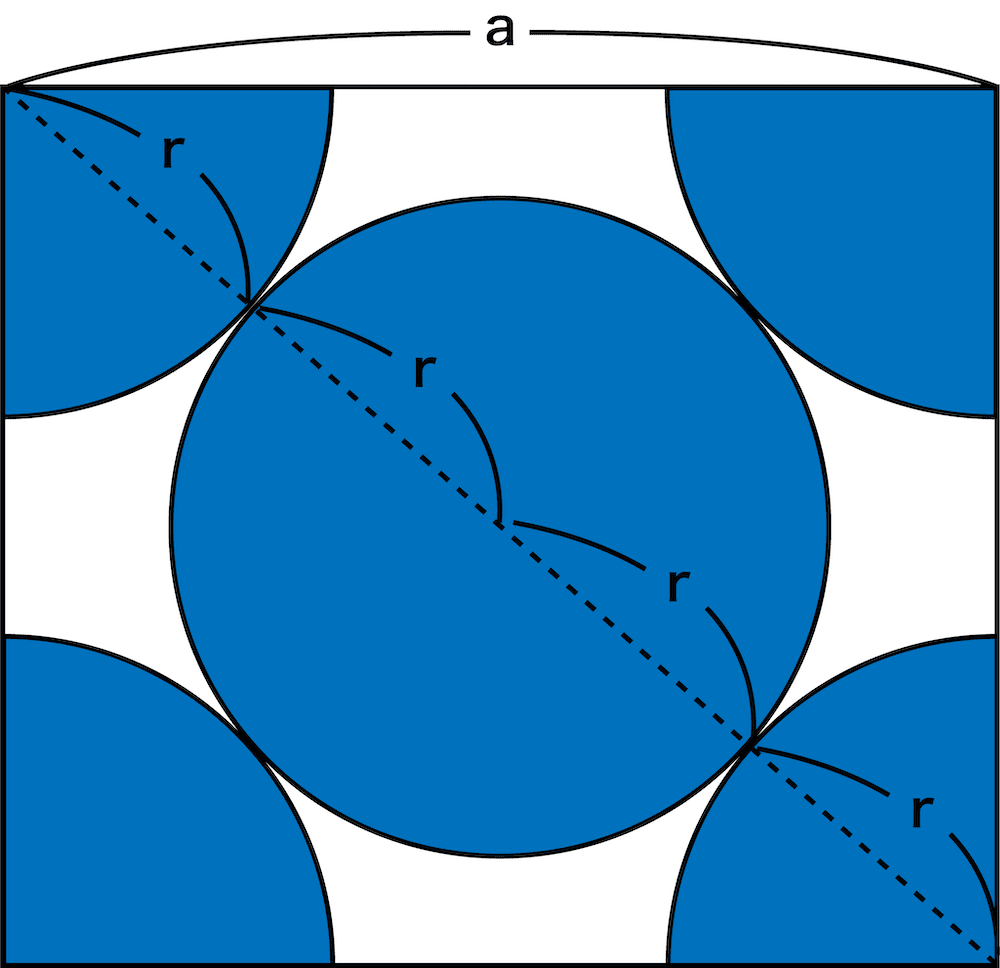
ここで、三平方の定理を用いると次のような式を立てることができる。
\[
(4r)^{2}=a^{2}+a^{2}
\]
これを整理すると、面心立方格子の格子定数と原子半径の関係を導くことができる。
\[
\begin{align}
(4r)^{2}=2a^{2}\\
\leftrightarrow 4r=\sqrt{ 2 }a\\
\leftrightarrow r=\frac{ \sqrt{ 2 } }{ 4 }a
\end{align}
\]
面心立方格子の充填率は【1】%である。
解答/解説:タップで表示
解答:【1】74
単位格子の体積に占める原子の体積の割合を充填率という。
\[
充填率=\frac{ 原子の体積 }{ 単位格子の体積 }×100
\]
「面心立方格子に含まれる原子の数」にあるように、面心立方格子は単位格子中に4個の原子を含んでいるため、次のような式を立てることができる。
\[
\begin{align}
充填率&=\frac{ 原子の体積 }{ 単位格子の体積 }×100\\
&=\frac{ \frac{ 4 }{ 3 }πr^{3}×4 }{ a^{3} }×100\\
\end{align}
\]
単位格子の1辺の長さ(格子定数)はaのため、単位格子の体積は(縦×横×高さで)a3となる。
また、球の体積は4/3πr3と表すことができる(これは数学の知識)ため、面心立方格子に4個の原子が含まれることを考えると、原子の体積の合計は4/3πr3×4となる。これを解くと、充填率は74%となる。
\[
\begin{align}
充填率&=\frac{ 原子の体積 }{ 単位格子の体積 }×100\\
&=\frac{ \frac{ 4 }{ 3 }πr^{3}×4 }{ a^{3} }×100\\
&=\frac{ \frac{ 4 }{ 3 }π(\frac{ \sqrt{ 2 } }{ 4 }a)^{3}×4 }{ a^{3} }×100\\
&=\frac{ \sqrt{ 2 }π }{ 6 }×100\\
&=74(\%)
\end{align}
\]














