MENU
結合エンタルピー（定義・計算問題の解き方など）
目次
はじめに
このページでは『結合エンタルピー（定義・計算問題の解き方など）』について解説しています。
結合エンタルピーとは
- 原子間の共有結合を切断するとき、および原子間に共有結合を形成するとき、熱の出入りがある。
- 気体分子間の共有結合1molを切断するために必要なエネルギーを結合エンタルピーという。
- 例えば、1molの水素分子H2を2molの水素原子Hとするためには、436kJのエネルギーが必要となる。このとき、H2中のH-H結合の結合エンタルピーは436kJ/molと考えることができる。
\[ \mathrm{H_{2}(気) \longrightarrow 2H(気)}~~~ΔH = 436\mathrm{kJ} \]
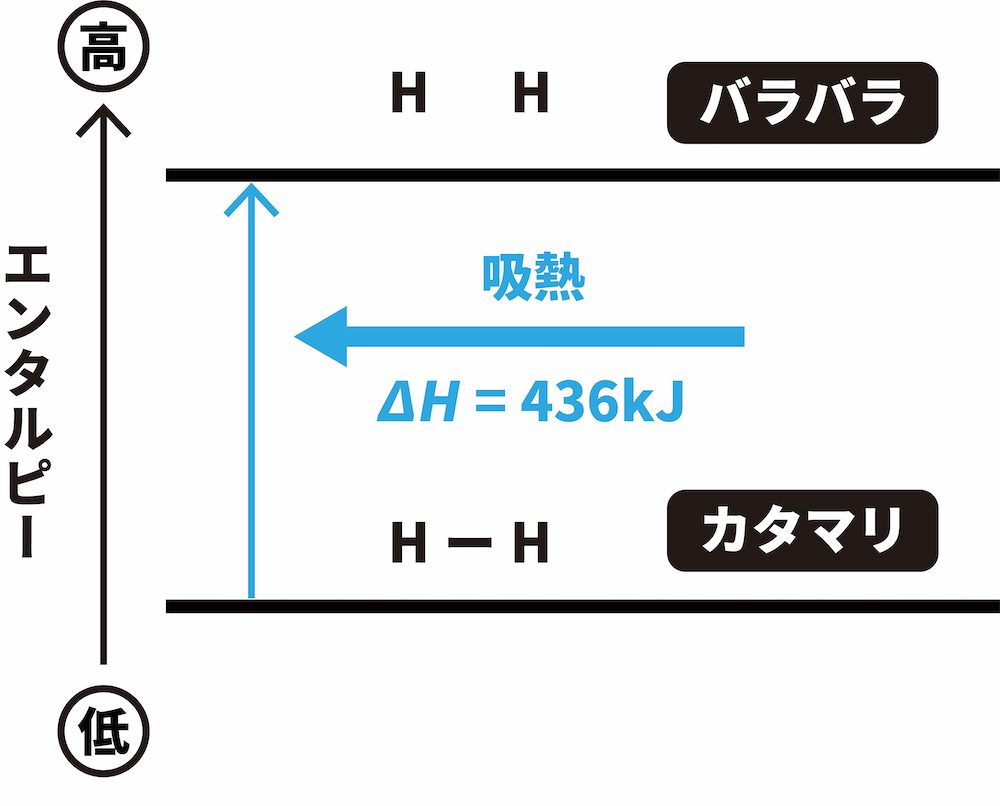
結合エンタルピーは結合を切断するために“必要な”エネルギーです。つまり、切断されるときにエネルギーが吸収されるので、結合を切断した後の“バラバラ”な状態のエンタルピーが、結合を切断する前の“カタマリ”の状態のエンタルピーよりも大きく、結合エンタルピーは正の値となります。
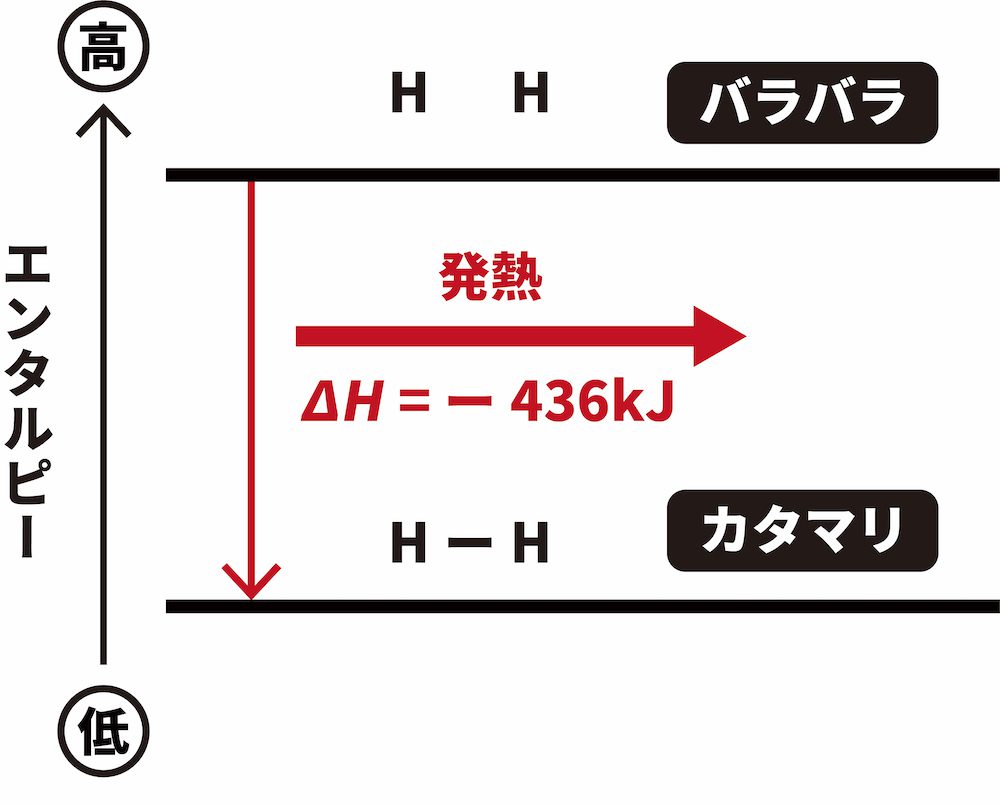
- 一方、2molのHが1molのH2となるときには、436kJのエネルギーが放出される。
\[ \mathrm{2H(気) \longrightarrow H_{2}(気)}~~~ΔH = -436\mathrm{kJ} \]
結合エンタルピーに関する計算問題
- 結合エンタルピーに関する計算問題の解き方について、例題を用いて解説する。
問題
塩化水素HClの生成エンタルピーを求めよ。ただし、HーH、ClーCl、HーClの結合エンタルピーをそれぞれ432kJ/mol、239kJ/mol、428kJ/molとする。
●STEP1
求める反応熱をQkJとし、それを含む熱化学方程式を書く。
●STEP2
STEP1でつくった式を元に、エネルギー図を書く。
●STEP3
図に書き込んだ分子を「バラバラ」の状態にし、エネルギー図の上の位置に書く。
●STEP4
それぞれの結合を切るために必要なエネルギーを書き込む。
●STEP5
ヘスの法則を利用して方程式を作成し、それを解く。
STEP
求める反応熱をQkJとし、それを含む熱化学方程式を書く。
求めたいのはHClの生成エンタルピーのため、HClの係数を1とし、他の物質の係数はそれに合わせる。また、求めたい熱量はQkJとする。
\[ \mathrm{\frac{ 1 }{ 2 }H_{2}(気)＋\frac{ 1 }{ 2 }Cl_{2}(気) \longrightarrow HCl(気)}~~~ΔH = Q\mathrm{\mathrm{kJ}} \]
STEP
STEP1でつくった式を元に、エネルギー図を書く。
H2とCl2という2つの物質がまとまってHClという1つの物質になるため、より「バラバラ」であるH2とCl2の方がエネルギーが高い。したがって、より高い位置に書く。
STEP
図に書き込んだ分子を「バラバラ」の状態にし、エネルギー図の上の位置に書く。
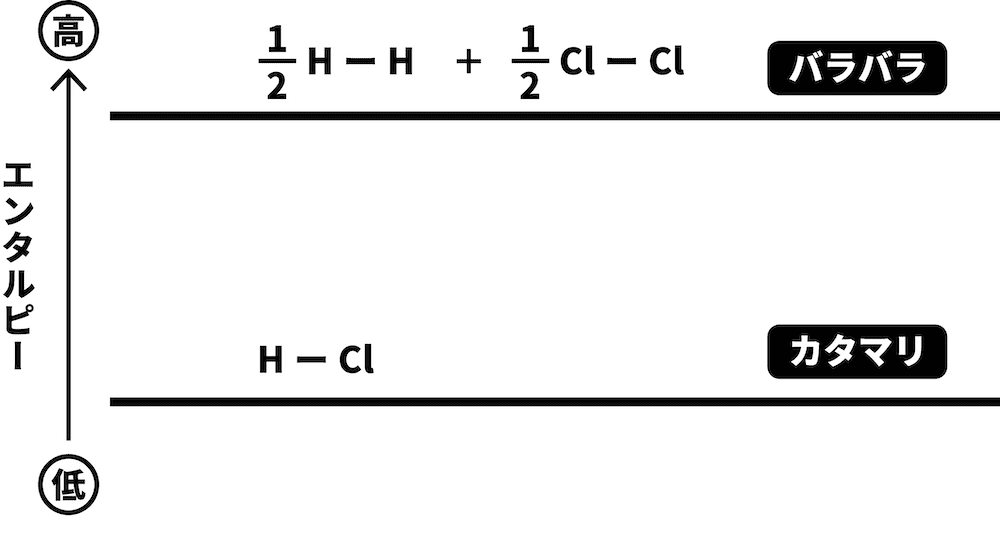
H2とCl2が、それぞれH原子とCl原子になった場合を考える。
STEP
それぞれの結合を切るために必要なエネルギーを書き込む。
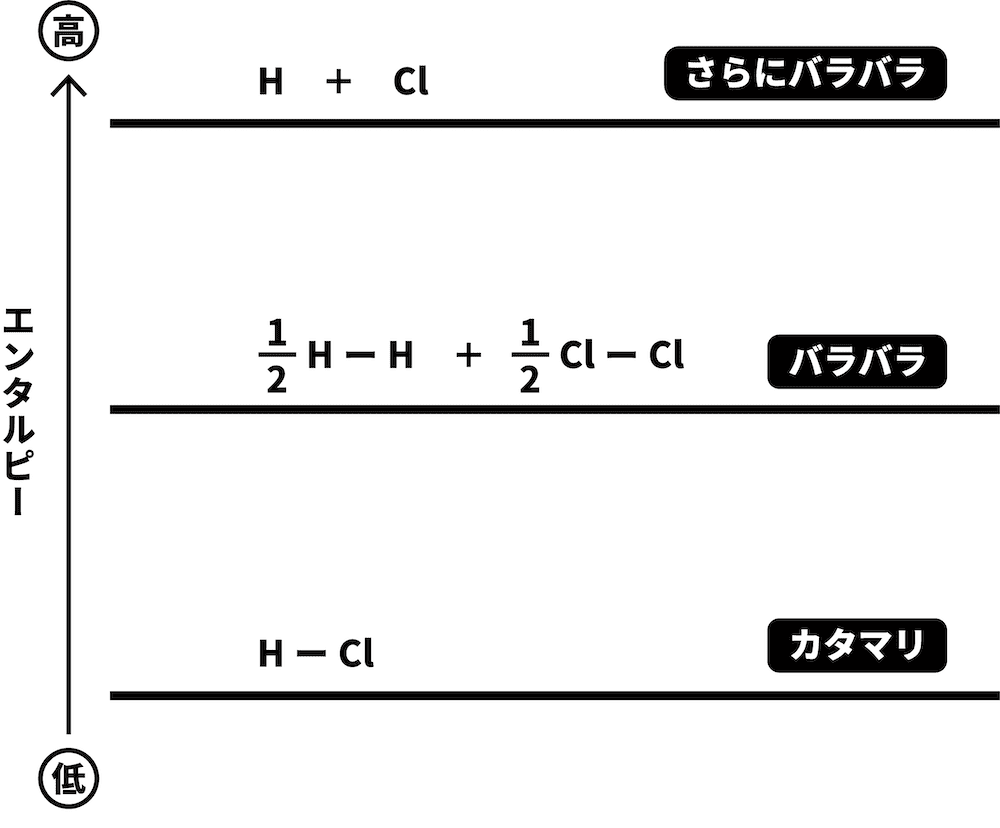
問題文に書いてあったHーH、ClーCl、HーCl結合の結合エネルギーを図中に書き込む。
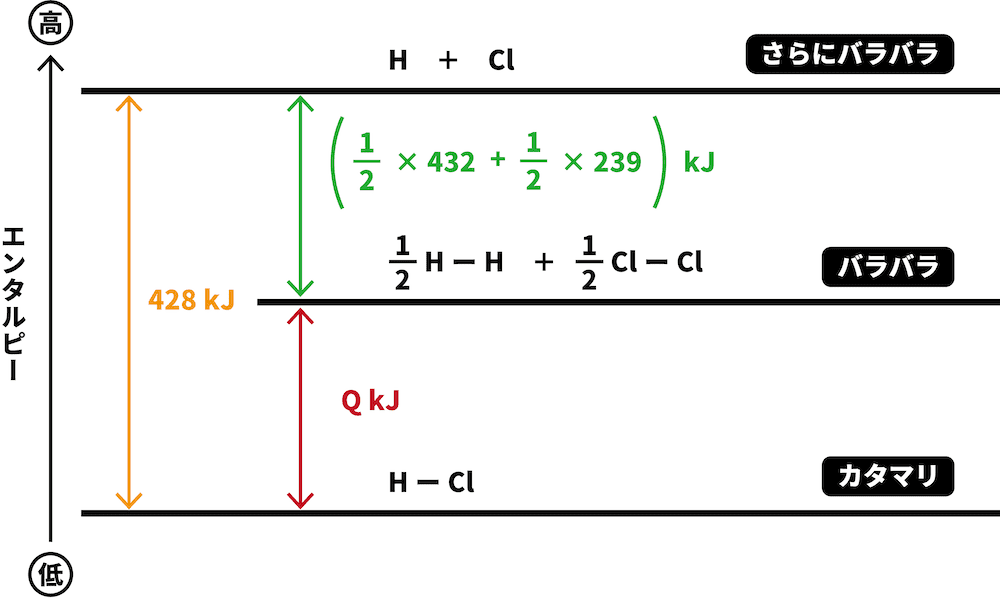
係数がついていた場合は、それをかけるのを忘れないように注意する。
STEP
ヘスの法則を利用して方程式を作成し、それを解く。
ヘスの法則により、化学変化に伴う反応エンタルピーは、反応前後の状態で決まり、反応経路によって変化しない。
参考：ヘスの法則（定義・反応エンタルピーの計算問題の解き方）
これを利用することで、次の式をたてることができる。
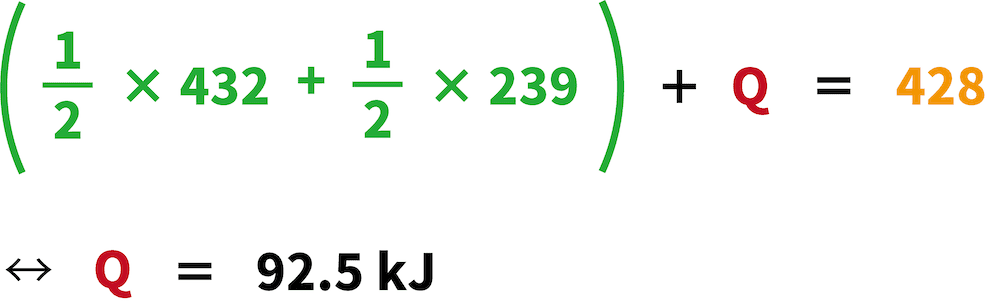
これが塩化水素HClの生成エンタルピーである。
【新課程対応】化学の計算ドリル大好評発売中！
高校化学・化学基礎の計算問題が苦手な人に向けた計算ドリルを発売しました。豊富な問題数で、入試頻出の計算問題の解き方を身につけることができます。
【新課程対応】無機化学ドリル発売中！
無機化学の知識を総ざらいできるオリジナル問題集ができました。解答・解説編には入試頻出事項が一通りまとめられており、まとめノート/参考書としての役割も果たします。
【新課程対応】有機化学ドリル発売中！
有機化学に関する入試頻出事項を演習することのできるオリジナル問題集が紙の本になりました。暗記項目だけではなく、計算問題や思考力が問われる問題についても触れています。
