MENU
水酸化ナトリウムの溶解熱(求め方・グラフを延ばす理由・熱化学方程式など)
はじめに
【プロ講師解説】このページでは『水酸化ナトリウムの溶解熱(求め方・グラフを延ばす理由・熱化学方程式など)』について解説しています。
水酸化ナトリウムの溶解熱
- 水酸化ナトリウムNaOHを水に溶解させると、溶解熱が発生する。
\[ \mathrm{NaOH(固)+aq \longrightarrow NaOHaq}~(Q\mathrm{kJ}の発熱) \]
- この溶解熱の発生により変化する液温を表すグラフを用いた問題が大学入試で頻出のため、今回はこのグラフの見方およびグラフが登場する問題の解き方を確認する。
水酸化ナトリウムNaOHを溶解することによる溶解熱の発生
- 水酸化ナトリウムNaOHを水に溶解した際の液温の変化を表すグラフを次に示す。
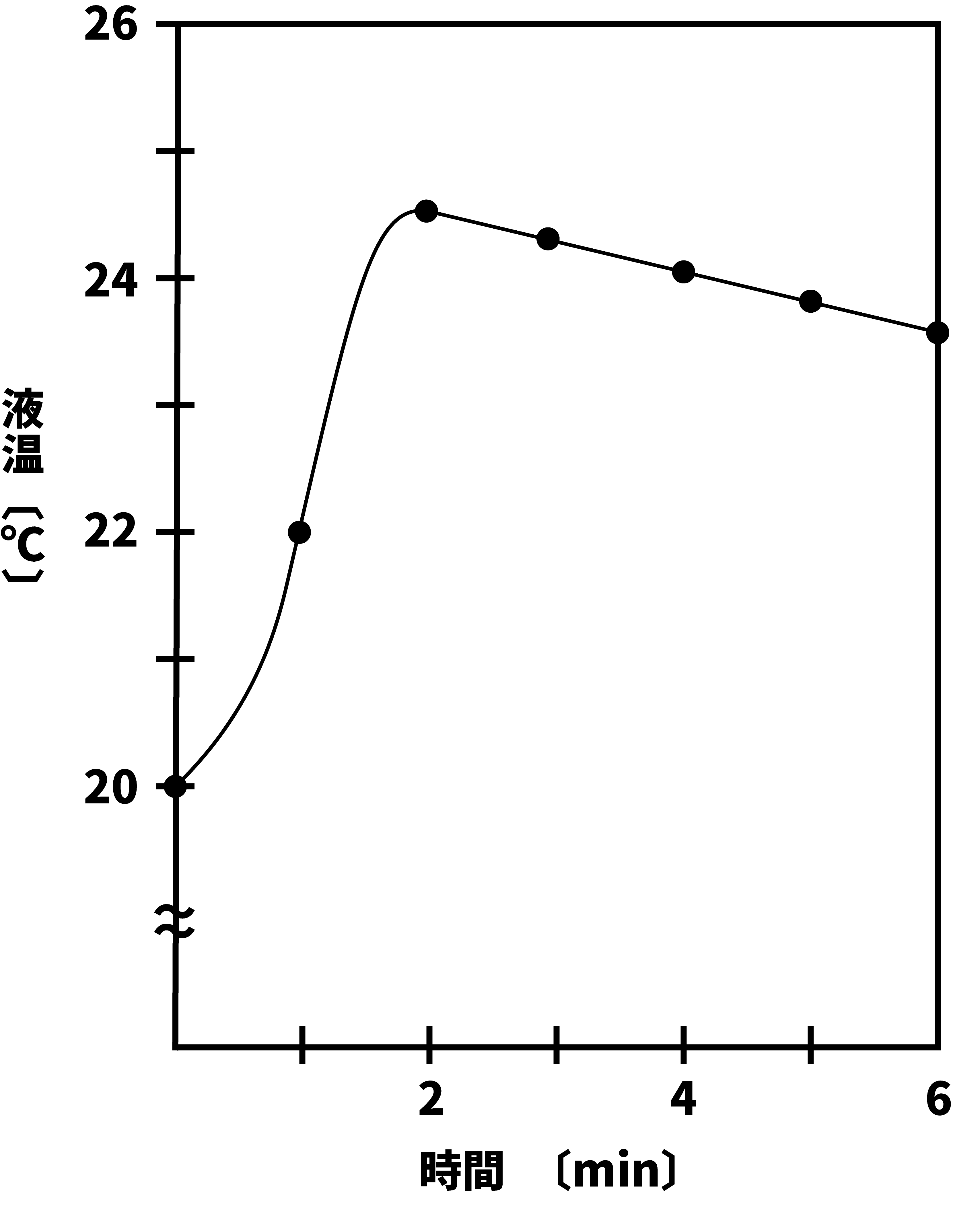
- このグラフの見方について、次の手順で解説する。
●STEP1
NaOHを水に加える。
●STEP2
NaOHの溶解は発熱反応であり、溶解熱が発生するため、反応が進むにつれ温度が上昇する。
●STEP3
NaOHが全て溶け切り、温度の上昇がストップする。
●STEP4
熱の発生がなく、熱は自然に放出されるため、温度は徐々に低下する。
まず、NaOHを水に加える。
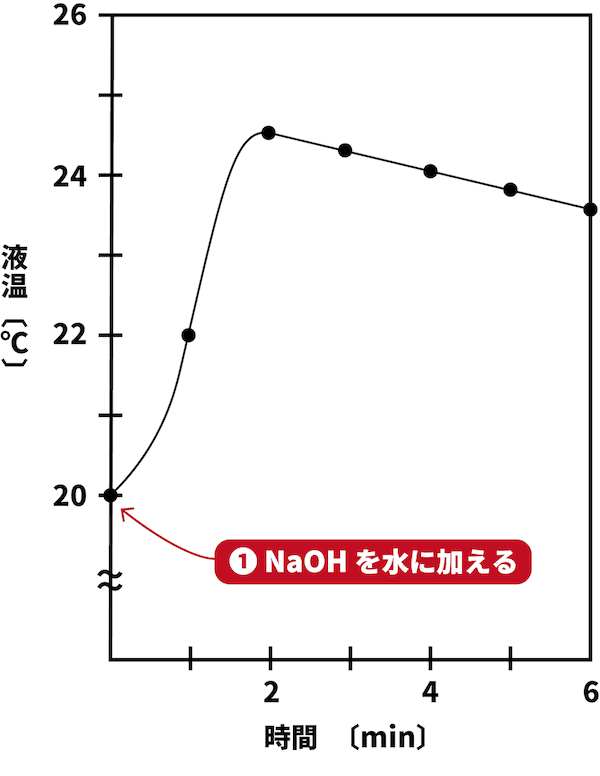
NaOHの溶解は発熱反応であり、溶解熱が発生するため、反応が進むにつれ温度が上昇する。
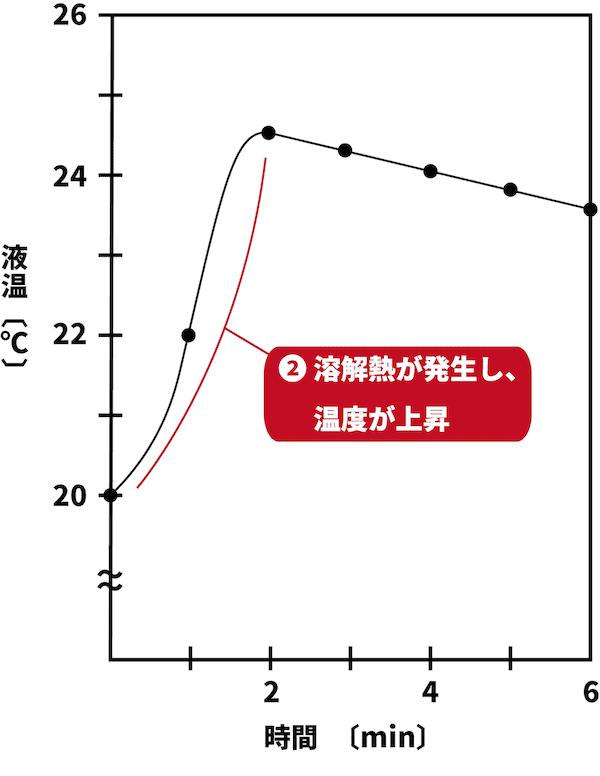
NaOHが全て溶け切り、温度の上昇がストップする。
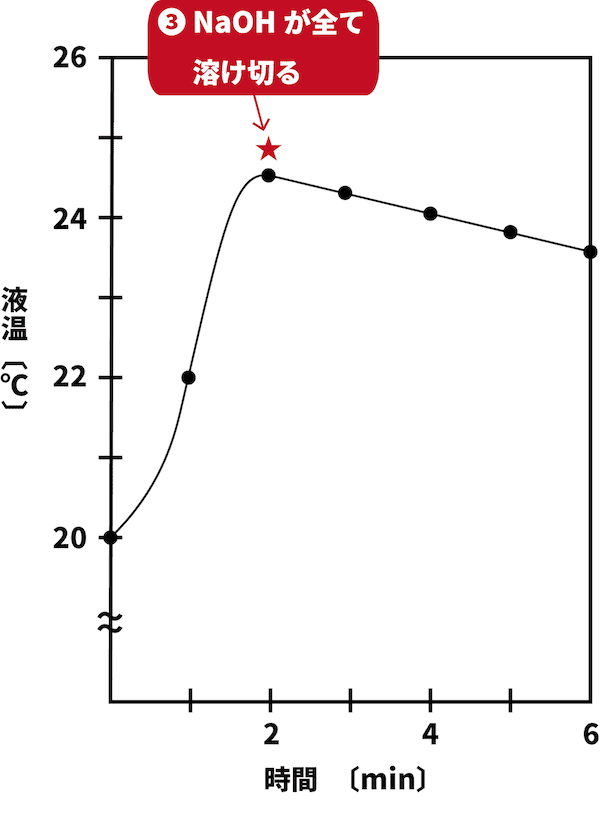
熱の発生がなく、熱は自然に放出されるため、温度は徐々に低下する。
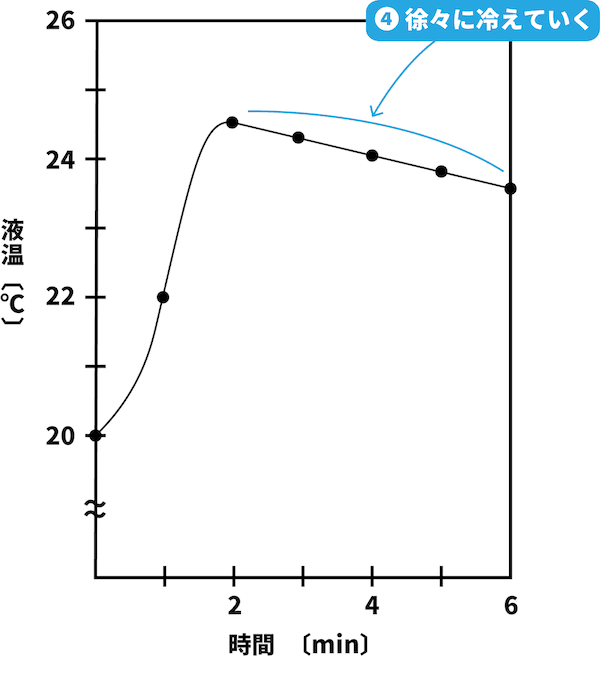
実際の最高温度を求める方法
- 「NaOHを溶解すると溶解熱が発生し、温度が上昇する」というのは間違いないが、実際は発生した熱の一部が(発生した直後から)徐々に外に逃げている。
- したがって、最高温度を考える際は、★の所をそのまま最高温度とするのではなく、「もし途中で一切熱が逃げなかったら(もしくは逃げる間もなく一瞬で溶解したら)」と仮定した温度に補正する必要がある。
- 補正は次の手順で行う。
●STEP1
放冷を示す直線を延長する。
●STEP2
温度を表す縦軸との交点をみる。
まず、放冷を示す直線を延長する。
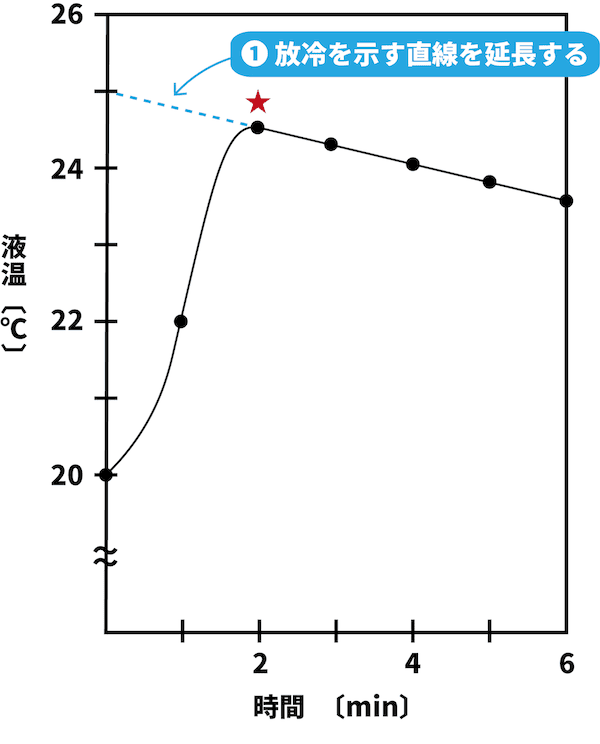
次に、温度を表す縦軸との交点をみる。
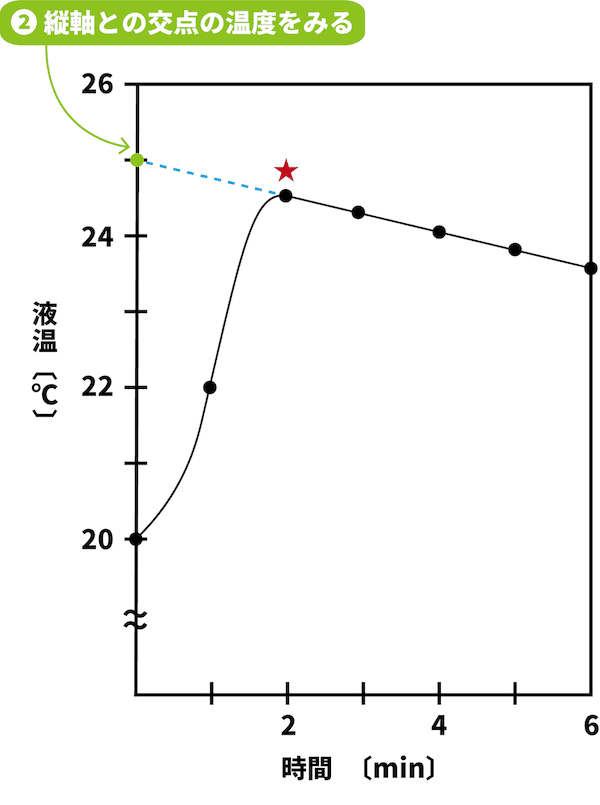
この交点の温度が、途中で一切熱が逃げなかった場合(もしくは逃げる間もなく一瞬で溶解した場合)の最高温度である。
水酸化ナトリウムの溶解熱に関する問題
- 水酸化ナトリウムNaOHの溶解熱に関する問題の解き方を解説する。
断熱容器に入れた水100mLに水酸化ナトリウムの結晶2.0gを入れ、よく撹拌した。次のグラフは、このときの時間ごとの温度変化を表したものである。次の問いに答えよ。ただし、水溶液の比熱は4.2J/(g・K)、水の密度は1g/mL、NaOHの式量を40とする。

(1)発生した熱量は何kJか(有効数字2桁で解答)。
(2)水酸化ナトリウムの水への溶解エンタルピーは何kJ/molか(有効数字3桁で解答)。
(1)
- まず、グラフの補正をすることにより、溶解時の熱の逃げがなかった場合の最高温度を求める。
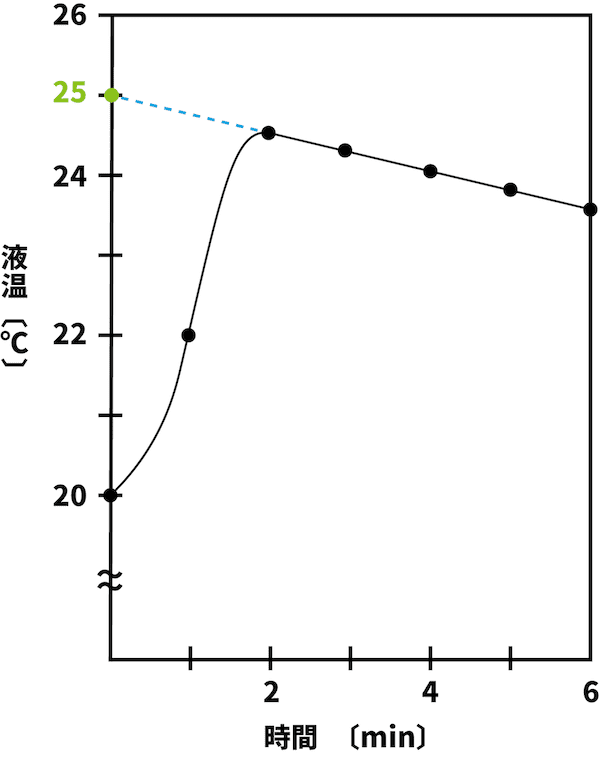
- 今回の場合、25℃である。
- 次に、熱量に関する公式を用いて、問われている熱量を求める。
熱量〔J〕=質量〔g〕× 比熱〔J/(g・K)〕× 温度変化〔K〕
参考:反応熱・エンタルピー・熱化学反応式(図解・比熱の計算など)
\[ \begin{align} 熱量〔\mathrm{kJ}〕&= 質量〔\mathrm{g}〕× 比熱〔\mathrm{kJ/(g・K)}〕× 温度変化〔\mathrm{K}〕\\
&=(\underbrace{2.0~\mathrm{g}}
_{\mathrm{NaOH}}
+
\underbrace{100~\mathrm{g}}
_{\mathrm{H_{2}O}})
×4.2×10^{-3}~\mathrm{kJ/(g・K)}×(25-20)~\mathrm{K}\\
&=2.142~\mathrm{kJ}\\
&\fallingdotseq2.1~\mathrm{kJ}
\end{align} \]
- よって、今回の実験で発生した熱量は 2.1kJ である。
(2)
- (1)で得た熱量をNaOH 1molあたりに換算する。
\[ \begin{align}
&2.142×\frac{1\mathrm{mol}}{\frac{2.0~\mathrm{g}}{40~\mathrm{g/mol}}}\\
&= 42.84~\mathrm{kJ/mol}\\
&\fallingdotseq 42.8~\mathrm{kJ/mol}
\end{align} \]
- よって、NaOHの水への溶解エンタルピーは ー42.8kJ/mol である。














